中2数学で習う一次関数。「xやyの増加量を求めなさい」という問題がよく出てきます。
一次関数は用語が多いうえに問題パターンが多いので、どうやって解けばいいのか混乱してしまいがちです。
そこで、この記事ではxやyの増加量の求め方について解説します、最後に練習問題も用意しているので、ぜひチャレンジしてみてください！
※関連記事：一次関数の変化の割合の求め方
まず、「xの増加量」「yの増加量」という言葉の意味からおさらいします。
増加量とは、「増えた量」と書きます。読んで字のごとく、「いくら増えたか」を指します。
例えば、「xの増加量が3」というのは「xが3増えた」という意味です。同様に、「yの増加量が4」であれば「yが4増えた」という意味です。
中学生にとってややこしいのは、「増加量をマイナス（-）で表す」ときがあるという点です。
例えば、「xの増加量が-3」「yの増加量が-2」のように表現します。それぞれ以下のような意味です。
このように、増加量をマイナスで表すときは「減った」という意味になります。
それでは、xやyの増加量の求め方を説明します。
xやyの「変化した後の値」から「変化する前の値」を引き算すると、xやyの増加量を求められます。
【公式】
（変化する前の値）ー（変化した後の値）
※x、yどちらもこの式で求められます
（例）xが「2から5」に変化した場合
変化した後の値：5
変化する前の値：2
↓
「変化した後の値」-「変化する前の値」
＝5-2
＝3
xの増加量：3
上記のように、xが「2から5」に変化しているので、5-2=3でxの増加量が3と求められます。yの場合も同じ解き方で求められます。
1次関数y=2x+1について、xが2から5に増加するときのyの増加量を求めてください。
yの増加量は6。
xやyの値がマイナスのときには、計算に注意が必要です。
（例）xが「-2から-5」に変化した場合
変化した後の値：-5
変化する前の値：-2
↓
「変化した後の値」―「変化する前の値」
＝-5-(-2)
＝-5+2
=-3
xの増加量：-3
上記のように、「-5-(-2)」の（ ）を外すと、-と-で+になります。この作業で間違いが発生しやすいので、慣れるまでは計算の途中式を書くようにすると良いです。
1次関数y=2x+1について、xが-5から-2に増加するときのyの増加量を求めてください。
yの増加量は-8。
増加量を求める問題のなかには、変化の割合を使ってxやyの増加量を求めるものも出てきます。以下のような、「変化の割合を求める式」を使って解きます。
「（変化の割合）＝（yの増加量）÷（xの増加量）」
この式に「変化の割合」や「xの増加量」「yの増加量」を入れます。
（例）y=2x+4という一次関数の式がある。xの増加量が3のときのyの増加量を求めなさい。
（変化の割合）＝（yの増加量）÷（xの増加量）
2=（yの増加量）÷3
（yの増加量）=3×2
（yの増加量）=6
「変化の割合」は「y=ax+b」の式の「a」を指します。上記の例では「2」が変化の割合です。
（変化の割合）＝（yの増加量）÷（xの増加量）の式に、問題文に書かれている数字をそのまま当てはめます。すると、求めたい数字が出てきます。
なお、変化の割合の求め方については以下の記事でくわしく解説しています。
一次関数の変化の割合とは（中学生）：変化の割合の求め方を解説（変化の割合を求める練習問題つき）
1次関数y=2x+1について、xの増加量が3のときのyの増加量を求めてください。
（変化の割合）＝（yの増加量）÷（xの増加量）
上の公式に、変化の割合2、xの増加量3を代入する。
2＝（yの増加量）÷3
（yの増加量）=2×3
（yの増加量）=6
yの増加量は6。
1次関数には「増加量」と「変化の割合」という用語がたびたび出てきます。それらの違いを簡単に説明します。
増加量は、xやyの変化そのものを指します。
具体的には以下のとおりです。
1次関数 y=2x+1の場合、xが2から5に変わるとき。
変化の割合は、xが1増えたときにyがどれだけ増えるか（yの増えるペース）を表します。
1次関数の式で言うと、以下の2にあたる数値です（xにくっついている数字）。
（例）y=2x+1
（変化の割合） =（yの増加量）÷（xの増加量）
1次関数 y=2x+1で、xが2から5に変わるとき：
つまり、この1次関数の変化の割合は「2」です。
図にすると、以下のようになります。
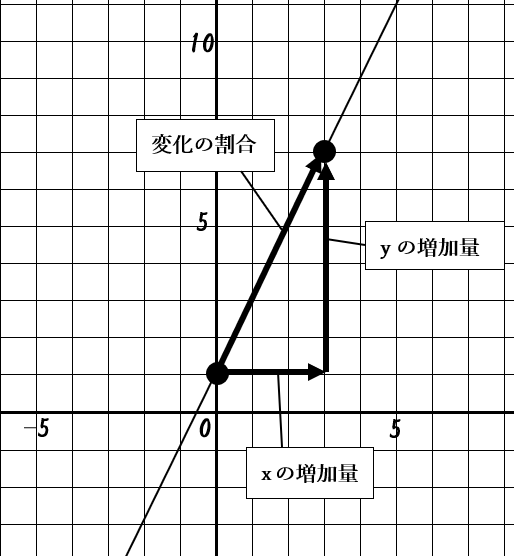
なお、この一次関数のグラフは傾き2で、切片が1です。傾きや切片の求め方については以下の記事でくわしく解説しています。
一次関数の傾きと切片：傾きや切片の求め方と一次関数の式の求め方を解説（練習問題つき）
実は、傾き「a」が分かっていれば、増加量を直接求められます。
「y=ax+b」の式の「ax」に「xの増加量」を代入するだけです。
例えばy= 3x+2の式で「xの増加量が4」の場合、「3x」に「x=4」を代入します。
3x=3×4=12
つまり、yの増加量は「12」だと分かります。
このように、「傾き」に「xの増加量」をかけるだけで y の増加量が分かるのです。
これが裏ワザ的な簡単な方法です。
一次関数y=3x+2において、yの増加量が9のとき、xの増加量を求めなさい。
答え：3
「（変化の割合）＝（yの増加量）÷（xの増加量）」の式をつかいます。
3=9÷（xの増加量）
（xの増加量）＝9÷3
（xの増加量）＝3
一次関数 y=5x−4yにおいて、yの増加量が15のとき、xの増加量を求めなさい。
答え：3
「（変化の割合）＝（yの増加量）÷（xの増加量）」の式をつかいます。
5=15÷（xの増加量）
（xの増加量）＝15÷5
（xの増加量）＝3
一次関数 y=−2x+7において、yの増加量が-4のとき、xの増加量を求めなさい。
答え：2
「（変化の割合）＝（yの増加量）÷（xの増加量）」の式をつかいます。
-2=-4÷（xの増加量）
（xの増加量）＝-4÷(-2)
（xの増加量）＝2
一次関数 y=1/2x+1において、yの増加量が3のとき、xの増加量を求めなさい。
答え：6
「（変化の割合）＝（yの増加量）÷（xの増加量）」の式をつかいます。
1/2=3÷（xの増加量）
（xの増加量）＝3÷1/2
（xの増加量）＝6
一次関数 y=−3/4x+5において、yの増加量が-9のとき、xの増加量を求めなさい。
答え：12
「（変化の割合）＝（yの増加量）÷（xの増加量）」の式をつかいます。
-3/4=-9÷（xの増加量）
（xの増加量）＝-9÷=(-3/4)
（xの増加量）＝12
一次関数 y=4x−2において、xの増加量が3のとき、yの増加量を求めなさい。
答え：12
（変化の割合）×（xの増加量）の式に数字を代入して解きます。
4×3=12
一次関数 y=−2x+6において、xの増加量が5のとき、yの増加量を求めなさい。
答え：-10
（変化の割合）×（xの増加量）の式に数字を代入して解きます。
-2×5=-10
一次関数 y=1/3x−1において、xの増加量が9のとき、yの増加量を求めなさい。
答え：3
（変化の割合）×（xの増加量）の式に数字を代入して解きます。
1/3×9=3
一次関数 y=−1/2x+4において、xの増加量が8のとき、yの増加量を求めなさい。
答え：-4
（変化の割合）×（xの増加量）の式に数字を代入して解きます。
-1/2×8=-4
一次関数 y=−4x+10において、xの増加量が2のとき、yの増加量を求めなさい。
答え：-8
（変化の割合）×（xの増加量）の式に数字を代入して解きます。
-4×2=-8
いかがでしょうか。中学生向けに、一次関数のxやyの増加量を求める方法を解説しました。
増加量は「変化の割合=yの増加量÷xの増加量」の式を使って解くと求められます。もしくは、yの増加量を求める問題なら変化の割合にxの増加量をかけるだけでも求められます。
どちらも慣れればすぐにできる方法です。
練習問題もつけていますが、もっと問題を解きたい人には下記の問題集がおすすめです。分野別に分かれているコンパクトな問題集なので、苦手分野の基本問題だけ演習したいときに便利です。
This website uses cookies.