一次関数の変化の割合の求め方と練習問題：変化の割合とは何か、傾きとの違い、変化の割合を求める公式など

Pocket

「一次関数の変化の割合が分かりにくい」

一次関数を苦手にしている中学生は多いですが、なかでも変化の割合がいまいちピンとこないとという中学生は少なくないでしょう。

ですが、変化の割合が分かれば一次関数の多くの問題、特にグラフのかき方や読み方がかなり分かりやすくなります。

そこで、中学生向けに一次関数の変化の割合について解説し、変化の割合を求める練習問題を用意しました。

【下記は難関高校受験に強いZ会のHPへのリンクです。リンク先で資料請求ができます。】
Z会　中学生コースの案内

※Z会について下記記事でくわしく紹介しています。
【中学生向け】Z会タブレットコースの進め方：成績上位を取って難関校に合格する方法を解説

一次関数の変化の割合とは

一次関数にはいくつもの用語が出てきます。そのなかの一つである「変化の割合」について解説します。

xが1増えるごとにyがいくら増えるかを表す値

変化の割合とは、「xが1増えるごとにyがいくら増えるかを表す値」のことです。

例えばxが1増えるごとにyが2ずつ増えていたら、「変化の割合は2」です。

y=ax+bのaが変化の割合

変化の割合は一次関数の式をみれば分かります。

y=ax+bのaが変化の割合です。

例えば、y=2x+3という式があれば、「変化の割合は2」です。

傾きと同じ意味

変化の割合以外に「傾き」という言葉も出てきます。傾きは変化の割合と同じです。

先ほどのy=2x+3の式だと、変化の割合は？と問われたら「2」になり、傾きは？と問われてもやはり「2」になります。

表でみるのかグラフでみるのかによってこうした言葉の違いが発生しています。

何はともあれ、「変化の割合＝傾き」と覚えておきましょう。

変化の割合の求め方

変化の割合について分かったところで、どのようにして変化の割合を求められるか説明します。

変化の割合の公式

変化の割合を求める公式があります。

「変化の割合＝yの増加量/xの増加量」

yの増加量をxの増加量で割ります。

例えばyの増加量が4でxの増加量が2だとすると、変化の割合は2です。

変化の割合を求める手順を説明します。

xの増加量を求める

まず、xの増加量を求めます。

増加量というのは「いくら数字が増えたか」です。以下の計算で求められます。

（変化した後のxの値）―（変化する前のxの値）

例えば、変化する前のxが3で、変化した後のxが5だとすると、以下の計算をします。

５－３＝２

つまり、xの増加量は2です。

yの増加量を求める

次に、yの増加量を求めます。yの増加量は以下の計算で求められます。

（変化した後のyの値）―（変化する前のyの値）

例えば、変化する前のyが4で、変化した後のyが8だとすると、以下の計算をします。

８－４＝４

つまり、yの増加量は4です。

yの増加量をxの増加量で割る

最後に、yの増加量をxの増加量で割ります。

先ほどの例ではyの増加量が4で、xの増加量が2でした。これを計算式に当てはめると以下の通りです。

４÷２＝２

つまり、xの増加量が2でyの増加量が4の場合、変化の割合は2になります。

グラフ上の2点の座標からも求められる

「yの増加量/xの増加量」の計算以外に、グラフ上の2点の座標から変化の割合を求める方法があります。

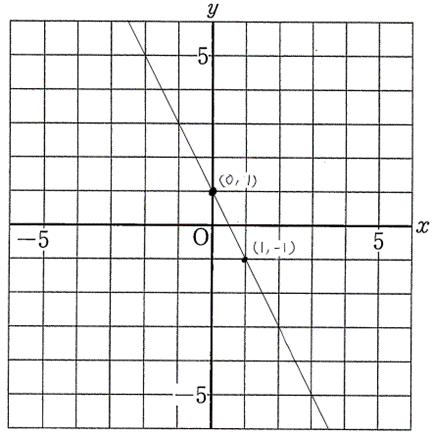
点（0, 1）から点（1, -1）までの移動の仕方を見ます。

点（0, 1）を出発して右に1マス進み、下に2マス進んでいることが分かります。つまり、xが1増えるとyは2減っているので傾きは-2です。

これはグラフから式をつくる問題で使う方法です。くわしくは一次関数のグラフのかき方や読み方の解説と練習問題で解説しています。

変化の割合を求める問題

変化の割合の求め方が分かったところで、実際に問題を解いて確認してみましょう。

問題(1)

y=2x+3の式で、xの値が2から5に増加するときの変化の割合はいくらですか。

解答

答え：2

解説：変化の割合はy=ax+bのaにあたる。xがいくつ増加したかは関係ない。

問題(2)

y=3x-1の式で、以下の場合のyの増加量を求めてください。

①xの増加量が2

②xの増加量が-2

③xが3から6に増加

④xが-2から4に増加

解答

yの増加量を求めるには「変化の割合」に注目する。変化の割合はy=ax+bのaなので、y=3x-1の式では「3」が変化の割合になる。

つまり、xが1増えるとyは3増えて、xが2増えるとyは6増えることになる。

切片の-1が気になりますが、変化の割合や増加量を求めるのに関係しません。

答え①：6

答え②：-6

答え③：9
xが3→6に増加しているということは、xの増加量は3

答え④：18
xが-2→4に増加しているということは、xの増加量は6

問題(3)

y=-2/3x+1の式で、以下の場合のyの増加量を求めてください。

①xの増加量が3

②xの増加量が-3

③xが1/2から5/2に増加

④xが-7/2から-1/2に増加

解答

①-2

②2

③-4/3

④-2

問題(4)

xとyの関係を表す次の表をみて、変化の割合を求めてください。

x	-3	-2	-1	0	1	2	3
y	-5	-3	-1	1	3	5	7

解答

答え：2

解説：xが1増えるごとにyがいくら増えているかをみる。
例えば、x=0のときy=1で、x=1になるとy=3になっている。つまりyは2増えている。

問題(5)

以下の直線の変化の割合を求めてください。

①y=-3/4x+2の式に平行で、点（3, 2）を通る直線

②2点（1, 3）（3, 6）を通る直線

解答

①-3/4
平行ということは、「変化の割合が同じ」。

②3/2
2点をくらべてxが1→3に2増加し、yが3→6に3増加している。
yの増加量/xの増加量の式に入れる。

中学数学の問題集

最後に、中学数学のおすすめ問題集を紹介します。

『中学10分間復習ドリル数学2年』

数学を基本からコツコツ復習したい人に向いているドリルです。

1日10分から基本問題の演習ができます。

中学10分間復習ドリル数学2年:サクサク基礎トレ! (受験研究社)

出版社：増進堂・受験研究社

『中学2年数学標準問題集』

基本レベルから応用レベルまで幅広く演習できる問題集です。

定期テストで平均点前後からスタートして90点くらいまでを目指せます。

中学2年数学標準問題集: 中学生向け問題集/定期テスト対策や高校入試の基礎固めに最適! (受験研究社)