「樹形図が書けない」
「すべての場合の数の求め方がバラバラでよくわからない」
確率でこのような不安を抱えている中学生は多いです。
数学のほかの単元とは解き方がまったく違っており、数学が得意な人も確率を苦手にしているケースがよくあります。
ですが、定期テストはもちろん、高校入試でも確率は必須単元です。
ぜひ得意にしておきたいですね。
そこで確率のポイントを確認して、
定期テストや高校入試に向けて短期間で得意にできる勉強方法を紹介します。
※関連記事：平面図形・空間図形の勉強方法
※関連記事：関数、比例・反比例の勉強方法
※関連記事：高校受験によく出る数学の文章問題
確率にはいくつかのコツがあります。
コツをつかんで、確率を得点源にしてしまいましょう！
この記事は下記の方向けです。
※スタディサプリについて下記記事でくわしく紹介しています。
スタディサプリ中学講座の特徴と効果的な活用法
まず、確率について軽くおさらいしましょう。
確率とは、
「あることがらが、どれくらい発生しそうかを表す数」
です。
小学校では下記の表し方をしました。
・何%
・何割
など。
中学校では「分数」で表します。
定期テストや高校入試で、
確率はどれくらい重要な分野なのでしょうか。学校の授業で確率分野はどれくらい扱うのでしょうか。
学校の年間カリキュラムの標準的な時間数を表にまとめました。
| 年間授業時間数 | 確率分野 | 確率分野の授業時間数 | 確率分野に使う授業時間割合 | |
| 中学1年生 | 140時間 | データの活用 | 15時間 | 11% |
| 中学2年生 | 105時間 | 確率 | 10時間 | 10% |
| 中学3年生 | 140時間 | 標本調査 | 9時間 | 6% |
学年によって多少の差はありますが、
年間10%前後ほどの授業時間数を確率分野に使っています。
高校入試ではどれくらいの配点になっているのかも確認します。
公立入試問題は都道府県単位で異なりますので、ここでは都立高入試でみてみます。
| 満点 | 90点 |
| 確率の配点 | 5点 |
| 確率の配点割合 | 6% |
学校の授業時間数にくらべれば高校入試での比重は小さいです。
ただし、確率が出題されるのは「小問集合」です。
志望校に合格するには、小問集合は取りこぼしたくない範囲です。
確率は単元の性質上、得意ならほぼ確実に点が取れます。
不得意だとこの5点分をほかの問題で取り返さないといけません。
配点は決して大きくありませんが、
合否をわけるポイントの1つなのです。
また、確率は高校での情報科の「データ分析」につながっていきます。
以前よりも重みが増しています。
確率がほかの単元とどうつながっているのか確認します。
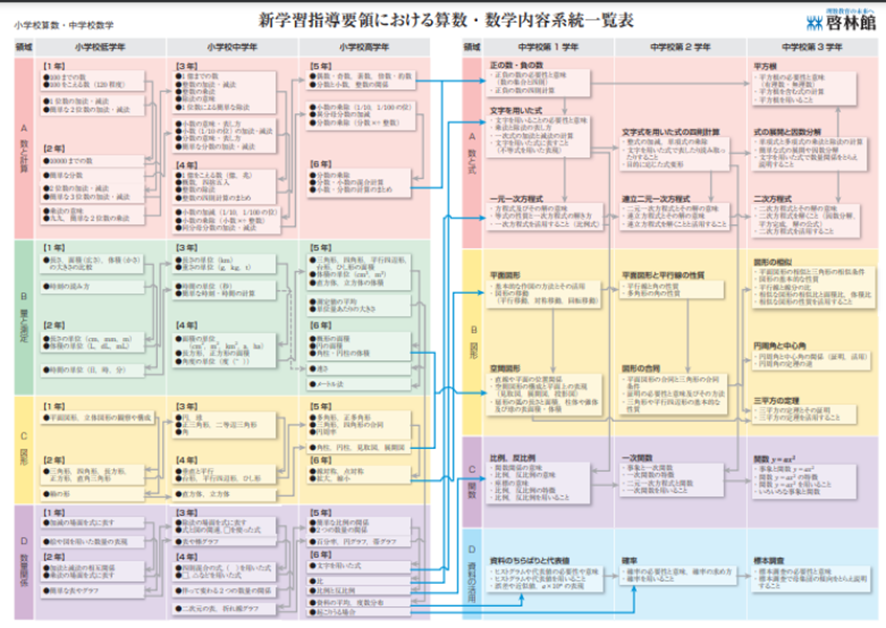
ご覧のように、「確率」はほかの単元から独立しています。
ほかの単元に関係していないので、
数学が苦手な人も「確率」を得意にしやすいです。
各学年で最後の定期テスト（学年末テスト）で出題されますから、それまで数学の成績がよくなくても最後に盛り返すことが可能です。
確率について大まかにわかったところで、
定期テスト対策・高校入試対策の方法を紹介していきます。
確率を苦手にしている人はたくさんいますが、実は数学が苦手な人でも高得点を取りやすい単元なのです。
確率が得意な人が実践している裏ワザの中から、すぐ実践できるものを3つ紹介します。
確率は「起こりうる場合の数」÷「すべての場合の数」で求められます。問題パターンごとに「すべての場合の数」を覚えておくと、確率を求めるのにかなり手間が省けます。
確率の問題は大体5つのパターンに分かれています。
| 問題パターン | すべての場合の数 | 説明 |
| 2つのサイコロを投げる問題 | 36 | サイコロの数字は1～6まであり、2個投げるので6×６=36 |
| 玉を取り出す問題 | すべての玉の数 | 赤玉2個、白玉3個ならすべての場合の数は5 |
| コイン（硬貨）を投げる問題 | コインの枚数の2乗 | コインを3枚投げるなら、3×3=9がすべての場合の数 |
| トランプの問題 | 52 | 1～13まで13枚のカードが4種類あるので13×4=52 |
| くじ引きの問題 ※くじを1回引く場合 | すべてのくじの枚数 | くじが5枚あるなら、すべての場合の数は5 |
確率では、「少なくとも～の事象が起こる確率を求めなさい」という問題がよく出てきます。定期テストでも20-30点くらいを占めることもよくあります。
この問題は「少なくとも」という条件があるため複雑に思えますが、実は単純な解き方です。「少なくとも～」の「～」以外の事象が起こる確率を求めて、1からその確率を引けばいいだけです。
例えば「サイコロを2回振って少なくとも1回は奇数が出る確率を求めなさい。」という問題があるとします。
「奇数が少なくとも1回出る確率」を求める問題ですから、逆に「奇数が1回も出ない確率」を求めて、1からその確率を引けば答えが出ます。
サイコロを2回振ったときの奇数や偶数が出る事象は下記の4通りです。
（奇数、奇数）
（奇数、偶数）
（偶数、奇数）
（偶数、偶数）
上記4通りのなかで「奇数が1回も出ない事象」は（偶数、偶数）の1通りだけです。全事象が4通りなので、「奇数が1回も出ない確率」は1/4。1から1/4を引けばいいので、
1-1/4=3/4
となります。よって、「奇数が少なくとも1回出る確率」は3/4です。
この問題だと、全事象を書き並べた時点で「3/4が正解だ」と気づけるかもしれません。「少なくとも～」の問題の解き方に慣れてくれば、このように早く解けるようになっていきます。
樹形図を描くときは、下記画像のように「若い順」に描きましょう。
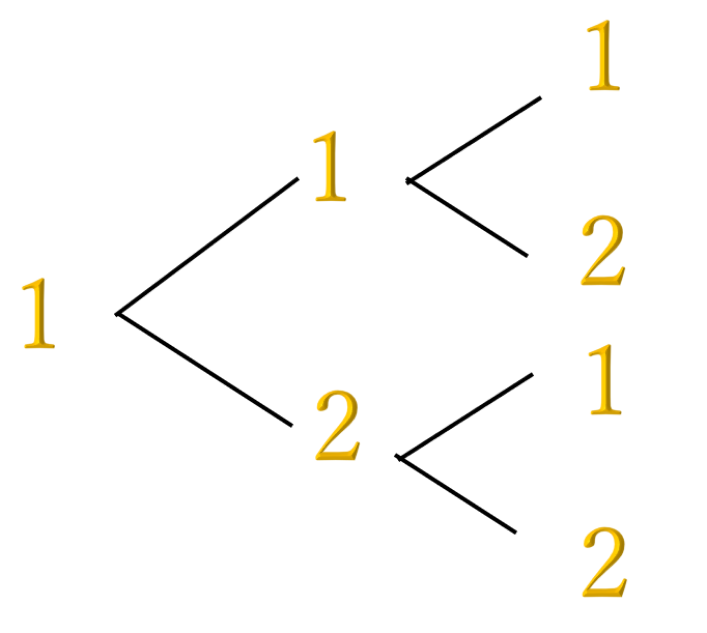
樹形図はとても便利ですが、「時間がかかる割に書きもれが起こりやすい」というデメリットがあります。書きもれた事象があると0点です。時間をかけて描いたのに0点だとテストでほかの問題を解く時間が少なくなりますし、心理的ダメージも大きいです。
1→2→3・・・
a→b→c・・・
のように、若い順に描くようにするだけで「書きもれ」がほとんどなくなります。
学習内容のポイントやコツを押さえたうえで、中学1年生から中学3年生まで学年別に定期テスト対策の仕方をお伝えします。
（単元・学習内容の名称は啓林館「新学習指導要領における算数・数学内容系統一覧表」より）
まず中学1年生の定期テスト対策の仕方をお伝えします。
中学1年では、「資料の散らばりと代表値」を習います。
学習内容は下記のとおりです。
| 学習内容 | ポイント |
| ヒストグラムや代表値の必要性や意味 | グラフの種類や表の作成方法 |
| ヒストグラムや代表値を用いること | 代表値の種類（平均値・中央値・最頻値）や、度数の種類・表し方を習う |
| 誤差や近似値、a×10nの表現 | 近似値、誤差、有効数字の意味を習い、 それらを使ってデータの扱い方を練習 |
学習ポイントごとに定期テスト対策の仕方をお伝えします。
【ヒストグラムや代表値の必要性や意味】
【ヒストグラムや代表値を用いること】
この2つの学習単元は、
資料の整理に必要な用語のインプットが中心です。
以下、表にまとめています。しっかりと覚えておきましょう。
| 用語 | 用語の意味 |
| ヒストグラム | データを長方形で表すグラフ。柱状グラフとも。 |
| 度数折れ線 | ヒストグラムの長方形の上辺の中点を線で結んだグラフ。 |
| 代表値 | 資料の特徴を1つの数値で表す、その資料を代表する値。平均値、中央値、最頻値にわかれている。 |
| 累積度数 | 最初の階級から各階級の度数を足した合計の度数。 |
| 累積度数分布表 | 累積度数をまとめた分布表 |
| 相対累積度数 | 最初の階級から各階級の相対度数を足した合計の相対度数（合計が1になる）。 |
用語→用語の意味を言えるようにするだけでなく、
用語の意味→用語も言えるようにしておきましょう。
【誤差や近似値、a×10nの表現】
この学習範囲のポイントは以下の2点です。
重要な用語とその意味を表にまとめています。
| 用語 | 用語の意味 |
| 近似値 | およその数 |
| 誤差 | およその数と真の値との差 |
| 有効数字 | 信頼できる数値 |
| 累乗の積 | 有効数字の表し方（10nのように表す） |
こちらも、用語→用語の意味を言えるようにするだけでなく、
用語の意味→用語も言えるようにしておきましょう。
有効数字の表し方はちょっと特殊です。
たとえば北海道の面積83424km2を有効数字2ケタで表すとすると、
8.3×104(km2)
となります。
ケタ数を「10n」で表すことで、数値の大きさをくらべやすくしているのです。
つづいて、中学2年生の定期テスト対策の仕方をお伝えします。
いよいよ本格的な確率の計算に入ります。最近まで高校入試で出題される確率は中2で習う範囲がほとんどでした。
中学２年では、「確率」を習います。
学習内容は下記のとおりです。
| 学習内容 | ポイント |
| 確率の必要性と意味、確率の求め方 | 確率とは何か・求め方、樹形図の書き方 |
| 確率を用いること | 確率を使ってサイコロやカードを引く問題を解く |
学習ポイントごとに定期テスト対策の仕方をお伝えします。
【確率の必要性と意味、確率の求め方】
場合の数を求めるために2種類の方法を覚えます。
樹形図は下記のように書きます。
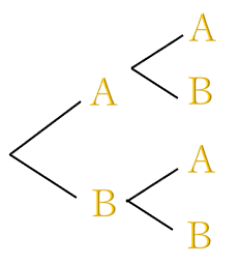
上記の例だと、
ABの3通りの組み合わせをすべて書き出し、一番右側の列を数えます。
書き出すときは、下記の順番に書くと抜け・もれが出にくいです。
また、表も便利です。
たとえば、2つのサイコロを振って
出た目の和（合計）が6になる場合の数を数えます。
下記のような表を書き、〇のついているセルの数を数えます。
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 〇 | |||||
| 2 | 〇 | |||||
| 3 | 〇 | |||||
| 4 | 〇 | |||||
| 5 | 〇 | |||||
| 6 |
確率は樹形図だけでも十分解けますが、
「2種類のものを組み合わせる場合」は、表のほうが抜けが出にくいです。
【確率を用いること】
確率の求め方を覚えて使えるようにします。
確率＝「あることがらが起きる場合の数」÷「すべての場合の数」
前述の、「2つのサイコロを振る例」だと、
出た目の和が6になる場合の数は5で、
すべての場合の数は36です。
確率は下記のように求めます。
確率＝5÷36
確率=5/36
問題はいくつかのパターンにわかれています。
コツは、パターンごとにすべての場合の数の求め方を覚えておくことです。
パターン別にすべての場合の数の求め方を紹介します。
①サイコロを振るパターンサイコロには目が6つあるので、
サイコロを振る数を6の累乗にします。
2回振るときは62、
3回振るときは63です。
②コインを投げるパターンコインは表と裏の2通りなので、
投げるコインの枚数を2の累乗にします。
2枚投げるときは22、
3枚投げるときは23です。
③玉を取り出すパターン「取り出す色の玉の数」を「袋のなかにある玉」で割ります。
袋のなかに8個の玉があり、
そこから赤玉を2個取り出すとすると、
2÷8＝ になります。
④トランプを引くパターンすべての場合の数は常に「52」になります。
トランプの数字と種類、色を覚えておきましょう。
| 数字 | 1～13 |
| 種類 | 4種類 （ハート、ダイヤ、クローバー、スペード） |
| 合計 | 52枚（13×4種類） |
| 色 | 赤（ハート、ダイヤ） 黒（クローバー、スペード） |
これをもとにして、
「あることがらが発生する場合の数」も考えます。
たとえば、
「ハート」なら13枚、
「黒」の「2」なら2枚（クローバー、スペード）です。
つづいて、中学3年生の定期テスト対策の仕方をお伝えします。
中学3年では、「標本調査」を習います。
学習内容は下記のとおりです。
| 学習内容 | ポイント |
| 標本調査の必要性と意味 | 標本調査の用語の暗記 |
| 標本調査で母集団の傾向をとらえ説明すること | 調査時の標本の選び方 |
学習ポイントごとに定期テスト対策の仕方をお伝えします。
【標本調査の必要性と意味】
ポイントは、「用語の暗記」です。
表にまとめています。
| 用語 | 用語の意味 |
| 全数調査 | 対象のすべてを対象にした調査 |
| 標本調査 | 対象の一部を体調にして全体を推測する調査 |
| 母集団 | 調査対象となる集団全体 |
| 標本 | 母集団から調査対象として取り出した一部 |
| 標本の大きさ | 取り出した資料の大きさ |
| 標本平均 | 標本の平均値 |
用語→用語の意味を言えるようにするだけでなく、
用語の意味→用語も言えるようにしておきましょう。
【標本調査で母集団の傾向をとらえ説明すること】
選挙速報など、日常生活でもなじみのある子が多いです。
ぜひ全問正解したい範囲です。
比例式を使うと計算間違いが減ります。
例えば、袋のなかに白と黒の碁石が合計400個あるとします。
20個取り出したら黒の碁石が5個だったとき、
袋のなかに黒の碁石が何個(x個)あるかを考えます。
400 : x = 20 : 5
20x = 2000
x=100（個）
外側の数字どうし、内側の数字どうしをかけ算します。
あとは、方程式と同じです。
定期テスト対策の勉強スケジュールを目標点数別にお伝えします。
定期テスト対策は、「広く」勉強するのがおすすめです。
特定単元をヤマ勘で勉強するのは効率よくありませんので、ご注意ください。
学校の授業に合わせて提出課題（ワーク）を進めましょう。
後でまとめて勉強すると、
暗記が多くなって追い付かなくなります。
授業で習ってすぐ提出課題で復習するだけでかなり記憶に残ります。
テスト1週間前までそれを続け、
ラスト1週間でもう1周しましょう。
提出課題とは別に教科書準拠の問題集を使うと、20点前後はアップします。
「確率」の定期テスト対策におすすめのドリル・問題集を2種類紹介します。AmazonのPRリンクをつけているので、リンク先でお得に購入いただけます。
どちらか1冊を仕上げれば十分ですが、
不安があれば2冊ともやってみましょう。
最初に紹介するのはくもんの「できた！」シリーズです。
学年ごとに、学校で習う順番どおり前半と後半に2冊ずつに分かれています。定期テストの問題と同じレベルの演習問題が並んでおり、テスト対策に使いやすいです。
こちらで紹介しているのは「後半部分」です。
中1向け↓
中2向け↓
中3向け↓
出版社：くもん出版
難易度：易～標準（★★☆）
特徴：
〔本書のねらい〕
基礎・基本が最初の一歩からよくわかるくもん独自のステップで，解きながら学ぶことができます。また，４択クイズアプリにより，テスト前にスマホで５教科の要点チェックができます。〔学習内容・特徴〕
くもん出版より引用
①基礎からのスモールステップと反復練習により，無理なく学習が進められます。
②豊富な練習量でなめらかなステップを実現することで，基礎力を確実に身につけます。
③未知のことを一方的に「教わる」のではなく，「例」や「空欄問題」を見て解き進めながら，自ら学びとることができます。
④発展的な問題も含んでいるので，高校入試対策の第１段階としてのベース作りができます。
⑤見やすい2色の解答・解説で「考え方」を確認し，理解を深めます。
つづいては旺文社の「得点アップ問題集」シリーズです。こちらも定期テストの問題と同じくらいの問題集演習が並んでいます。
特徴は、テスト前の1週間で対策できるような分量にしているという点です。
1日ごとにこのページを勉強しましょうと分けてくれており、「どこから勉強すればいいか」「どれくらい勉強すればいいか」を考える必要がありません。
中1向け↓
中2向け↓
中3向け↓
出版社：旺文社
難易度：易～標準（★★☆）
特徴：
中学校の定期テスト対策を、1日30分×7日間を目安として短期完成できる問題集です。
■各単元の構成は、STEP1要点チェック・STEP2基本問題・STEP3得点アップ問題の３ステップで、段階的に定期テストの得点力が身につきます。
STEP1 要点チェック 単元の大事な学習ポイントをまとめています。
STEP2 基本問題 基本的な問題で単元の内容を確認できます。
STEP3 得点アップ問題 定期テストの問題形式にならった単元の総仕上げ問題です。■スケジュールの目安が示してあるので、定期テストの範囲を１日30分×7日間で、計画的にスピード完成できます。
旺文社より引用
■コンパクトで持ち運びしやすい別冊「＋10点暗記ブック」＆赤セルシートで、いつでもどこでも、テスト直前まで大切なポイントを確認できます。
80点以上を目指すなら、
応用問題を解けるかどうかがポイントになります。
前述の学習ポイントをすべて押さえておくと80点を取る実力が身につきます。
テストでミスをしない・制限時間内に解く力を養いましょう。
まず、平均点を目指す場合と同じく、
学校で習った日に提出課題を進めます。
提出課題以外に、ハイレベルな問題集を1冊準備しておきましょう。
テスト2週間前になったらそのハイレベルな問題集をスタートします。
テストまでにテスト範囲を2周しておきましょう。
80点以上を目指す人におすすめの定期テスト対策用の問題集を紹介します。
最初は「チャート式」です。
参考書編と問題集編に分かれており、参考書編は単元のポイントを丁寧に解説して理解しやすくしています。参考書編をみながら問題集編を解くと、「どこを参照すれば良いか」が分かりやすく勉強しやすいです。
どの学年も1冊200ページ以上もあり、問題量が豊富です。
中1：参考書編↓
中1：問題集編↓
中2：参考書編↓
中2：問題集編↓
中3：参考書編↓
中3：問題集編↓
出版社：数研出版
難易度：標準～難（★★★）
特徴：
日常学習から入試対策まで充実の1冊！
教科書の内容からていねいに説明し，公立高校入試レベルまで着実に力をつけることができる参考書。
数研出版より引用
考え方や問題の着眼点，注意事項などをていねいに説明し，思考力を養うことができる。単元の要点を説明する解説動画や，計算問題をカード形式で反復練習できる計算カードなど，デジタルコンテンツを利用した学習ができ，自学自習にも最適。入試対策編では入試頻出の問題をおさえてから，入試レベルの問題に取り組むことができる。
数学を苦手にしている中学生から実力UPを目指す中学生まで多くの中学生にオススメ。
つづいては「最高水準問題集」です。
タイトルどおり、難易度の高い問題中心の問題集です。定期テストで出てこないようなハイレベルな問題も掲載されています。
そうした発展問題も解けるようにしておくと、定期テストでミスをしにくくなります。
中1用はコチラ↓
中2用はコチラ↓
中3用はコチラ↓
出版社：文英堂
特徴：
難関高校の入試問題で実力強化
国立・私立難関高校の入試問題から質の高い良問を精選しました。トップレベルの実力を身につけることができます。難問・超難問も多数掲載
私立難関高校で出題された難問・超難問も多数掲載しています。超難関高校の入試対策は万全です。選択学習しやすい表示
文英堂より引用
各問題には1～3個の★でレベルを表示しています。また、入試によく出る問題には「頻出」マーク、とくに難しい問題には「難」マークをつけています。学習時間・実力に合わせた使い方ができます。
入試対策に本格的に入るのは中学3年生からという人が多いと思います。
そのときには、以前習った内容を少し忘れてきています。
下記の順に勉強するとスムーズです。
たいていの入試対策問題集は、
この順に勉強するようにできています。
高校入試で「確率」の出題パターンは少ないです。
非常に勉強しやすいので、確実に得点できるよう慎重に勉強しておきましょう。
頻出パターンごとの勉強方法をお伝えします。
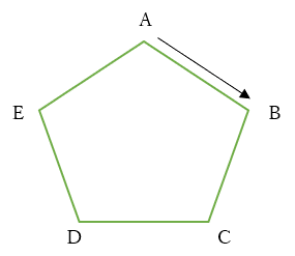
上記の図で、サイコロを3回振ります。
点Pが点Aから出発して、
出たサイコロの目の数だけ右回りに進みます。
3回振って点Pが点Aに戻ってくる確率を求めます。
こういう問題の場合、下記の手順で解答します。
1. すべての場合の数サイコロなら6の累乗で求められます。
すべての場合の数＝63
=216（通り）
2. あることがら点Aから出発するので、
5マス進めば点Aに戻ってきますね。
3回目で点Aに戻るには、
3回振って出た目の和が5の倍数になればＯＫです。
1回で最大6までなので、
5、10、15
の3通りが該当します。
3. 計算する3÷216=3/216
ほかにも、円周の問題もよく出ます。
解き方は同じです。
①すべての場合の数
②あることがらの場合の数
③②÷①を計算
これで求められます。
単元別・頻出問題別に演習をしたら、
いよいよ総合問題や過去問で演習しましょう。
複数の単元をまとめた問題の演習です。
各問題集の最後に掲載されているか、
分厚い問題集だと2-3つの単元ごとに復習問題として掲載されています。
【目的】
単元ごとの知識を整理してアウトプットできる力を養う。
【おすすめの学習量】
少なくとも5回分は解きましょう。
【ワンポイント】
複数単元を1度に解こうとすると、解き方を思い出すのに苦労することがあります。
下記の順に演習してみましょう。
総合問題集は、志望校の難易度にあうものを選びましょう。
にわけて問題集を紹介します。
〇偏差値55くらいまで
偏差値55くらいまでの中堅校の対策に便利な問題集を2冊紹介します。
数学は解法だけでなく「なぜその解き方をするのか？」という「考え方」を大事にすると伸びやすくなります。
この問題集はそういう「解き方（考え方）」をしっかりと解説してくれている問題集です。
ほかの問題集で「解説を読んでも、解く手順は分かるけどなぜそう解くのかピンとこない」という人におすすめです。
出版社：旺文社
特徴：
「暗記では解けない問題の解き方」を身につける！
★「出題頻度が高い」＆「解き方にコツがある」問題をマスターして得点アップ！
公立高校入試の問題は、難度の幅が広く、暗記で解ける問題と解き方（考え方）が必要な問題があります。一部の問題は演習量よりも、解き方を押さえてから演習したほうが効率的に点数を上げることができます。本書で選んだ問題をマスターすることで、入試の得点アップにつながります。★徹底的に「解き方」に焦点を当てた解説！
旺文社より引用
「例題」「解き方チェック問題」「実践問題の解答解説」のすべてで「解き方」のチェックポイントに沿った解説をしています。
こちらの問題集は、「公立高校入試向けに標準レベルの問題ばかり」を集めた問題集です。
入試数学では難易度の高い問題も出てきますが、ライバルと差が開くのはむしろ「標準レベルの問題」です。50%以上の受験生が正解できるレベルの問題を100%正解すれば、それだけでライバルより10点程度高い点数を取れます。
出版社：旺文社
特徴：
全国の公立高校入試の配点データを分析し、中配点・中難度の過去問に厳選した問題集です。学習効果が最も出やすい「標準問題」を確実に解く力をつけることを目的として、各課を「要点まとめ + 過去問演習」で構成し、理解と定着を交互に行うことができます。
以下のような方に特におすすめです。
旺文社より引用
・公立高校を第一志望にしている。
・基本事項ならある程度は覚えている。
・全範囲をまんべんなく解けるようになりたい。
・１冊の問題集をやり切って実力をつけたい。
〇偏差値55以上
偏差値55以上で、特に難関高を志望している人向けに2種類問題集を紹介します。
人気のチャート式問題集です。
公立高校入試レベル～難関国公立・私立高校入試レベルまでカバーしています。
全50回のテストで段階的に学力を伸ばせる設計なので、何度も間違う苦手単元の発見にも役立ちます。
出版社：数研出版
特徴：
難関高校を受験する人に最適な、入試本番を見据えた実戦的な問題集。
Amazonより引用
問題はランダム配列で、1回5問の実戦テスト形式です。目安時間もあるため、本番を意識した実戦的な勉強ができます。問題のレベルによって「標準」「発展」「難関」の3段階のコースに分かれており、実力に応じた演習が可能です。標準は15回分の公立高校入試レベル、発展は15回分の中堅私立高校入試レベル、応用は20回分の難関国公立・私立高校入試レベルの問題を掲載しています。別冊解答編には、問題の答のほか問題の考え方や詳しい解説を掲載しています。解法の過程を確実に押さえることで、難問に対するアプローチの仕方が身につきます。本冊112ページ、解答編152ページ。
この問題集は難関国立・難関私立高校入試対策の定番です。
発展問題中心に構成されており、定期テストで80点以上を取っている人でようやく少しずつ使いこなせるレベルです。
各問題に「難」「頻出」「新傾向」とマークをつけてくれているので、自身の志望校の入試問題にあわせて選択できます。
単元別問題で弱点を補強しておき、
チェックを兼ねて総合問題で仕上げができます。
難問ぞろいなので、初見で解けない問題もたくさんあります。
出版社：文英堂
特徴：
過去の入試問題を徹底分析
国立・私立難関高校の入試問題を全分野から厳選。よく出る問題には「頻出」マークを、特に難しい問題には「難」マークをつけて、問題を解きながら、問題のレベルや傾向がわかるように配慮しました。重点的に強化できる単元別の配列
各自の学習計画に合わせてどこからでも学習できます。また弱点分野の補強や、入試直前の重点演習もできます。入試対策総仕上げのための模擬テスト
文英堂より引用
入試本番を想定した模擬テストを巻末につけました。志望校突破のための最終チェックができます。
※関連記事：数学80点以上の人向けおすすめ問題集と勉強方法
総合問題演習が終わったら過去問演習に入りましょう。
過去問ばかり集めた問題集を使います。
【目的】
入試で1点でも高く取れるように練習する。
【おすすめの学習量】
少なくとも5回分は解きましょう。
【ワンポイント】
下記の2点を実践してみましょう。
制限時間内に1点でも高い点数を取れるようにします。
大問を1つ解くごとに時計を確認し、
残り時間でどの問題を解けば少しでも高い点数を取れるかシミュレーションを繰り返しましょう。
中学3年生の長期休み（春・夏・冬）には、
高校入試対策をしておきましょう。
おすすめの高校入試過去問題集を紹介します。
高校入試対策にはやはり「過去問」が欠かせません。ただ、いきなり過去問を通しで解いても単元によっての得意・不得意があると、うまく過去問で点が取れません。
1年分を解く前に「分野別」に過去問を解いて練習しておくと便利です。
数と式・関数・データ活用↓
図形↓
出版社：旺文社
特徴：
21-23年の公立高校入試問題を厳選し、分野別に並べ替えた問題集。類似した問題が複数の都道府県で出題されていることが一目瞭然で、出題傾向・出題パターンがわかります。よく出題されている問題を数多くこなすことで、入試に即した対策をすることができます。 ※本書では数と式・関数・データの活用の3分野を収録しています。
Amazonより引用
分野別の勉強が終われば、1年分を通しで解いてみましょう。
出版社：東京学参
特徴：
2024年高校入試より数学の問題と解答解説を掲載。47都道府県の公立高校と主な国立・私立および高等専門学校を収録。都道府県別・高校ごとに「出題傾向と対策」、問題ごとにくわしい「解き方」を解説。最新の高校入試問題を系統別に分析・学習できる入試対策必須の一冊。思考力を問う問題には、思考力マークを表記。
Amazonより引用
多くの中学生は単元ごとで得意・不得意が分かれます。数学の勉強を効率良くするには、単元ごとの得意・不得意に合わせて問題のレベルを変えるのがおすすめです。
大手の通信教育なら問題の正解・不正解に応じて「解くべき問題」を提示してくれる機能があります。定期テストにも高校入試にも対応しており、難関校入試専用の講座も備えています。
勉強を得意にするには「分かりやすい授業」を「何度も受けること」が近道です。
スタディサプリは高品質な授業動画に加えて10万問以上の演習問題があり、月10,780円で個別指導も受けられます。
くわしくは、スタディサプリ中学講座の特徴と効果的な活用法で紹介しています。
やはり通信教育といえば進研ゼミです。受講者数No. 1で、昔から高校受験対策に定評があります。
高校入試情報をタイミングよく配信してくれますし、苦手克服から難関校対策まで幅広いレベルに対応しています。解説動画を学校の予習代わりに使って1日15～30分の勉強で高得点をねらうことも可能です。
くわしくは、進研ゼミ中学講座の特徴と効果的な利用法で紹介しています。
定期テスト対策や高校入試対策の王道として、塾の活用を考えてみましょう。
子どもは「人からの影響」を強く受ける時期にいます。
といったメリットが塾にはあります。
時期や生徒の学習状況・志望校・学力目標に応じて必要なカリキュラムを考えても、肝心の本人が実行しなければ（実行し続けなければ）効果は薄くなります。
「人からの働きかけ」と「学習環境」によって子どもの学習行動や意識は変わります。
※関連記事：塾はいつから通う？費用は？
こういうときは、家庭教師が便利です。特に受験直前期に家庭教師を活用する方が多くなります。
また、最近ではオンライン家庭教師の優位性がかなり際立ってきています。
普段は塾や予備校で教えている指導者がプロ家庭教師として活躍しています。オンラインなので、移動圏外に住んでいる人がちょっと空いた時間に授業をしています。
トップクラスの実績を持つプロ講師に教われば、1人であれこれ工夫するより5倍10倍早く、的確にポイントを押さえた学習ができます。
特に社会はプロと学生で指導力に大きな差が表れる科目です。「暗記科目」だと思うと興味がわきにくいかもしれませんが、プロが教えると興味を持つようになって楽しく勉強できるようになることがよくあります。
アプリはちょっと調べたいときに、手軽に勉強に使えます。
2種類紹介します。
Appストアでみる
Google Playでみる
評価：Appストア4.6、Google Play4.3
ダウンロード数：10万以上
課金要素：無料
※広告表示あり
スクリーンショット：
特徴：
中学数学、高校数学の重要公式をカンタンに確認できるアプリが新登場！
各公式ページについている、公式の利用シーン、公式の覚え方・使い方などの、お役立ち解説は必読！
このアプリで中学数学、高校数学の重要公式をしっかり確認しよう！公式は、中学数学（数と式、関数、図形）、高校数学（数学Ⅰ、数学A、数学Ⅱ、数学B、数学Ⅲ）の分野別に収録。
アプリ内の検索機能で公式を検索することもでき、とても便利です。本アプリ「数学公式集（中学数学・高校数学の公式解説集）」は無料です。
収録内容について何かあれば、アプリ内のお問い合わせからご連絡ください。
Appストアより引用
【おすすめする理由】
ふと公式を忘れたときにさっと調べてすぐに練習できます。
公式の使い方も解説してくれます。
無料で利用できるのもありがたいです（広告表示あり）。
Google Playでみる
ダウンロード数：100以上
課金要素：無料
※広告表示あり
スクリーンショット：
特徴：
高校入試対策にぴったりな問題集アプリが登場！
アプリで問題を見ながら、ノートに解くスタイルのアプリです。■ “基礎がため”から”過去問演習”まで
スキマ時間にサクサクできる「一問一答」の問題から、実戦力が身につく「高校入試問題」まで、幅広い難易度の問題を掲載しています。■ アプリが君のニガテを記憶する！
「ニガテ克服機能」を使えば、類題演習が簡単にできます。
効率的にニガテをなくしたい方にオススメです。■ すべての問題にポイント解説つき
Google Playより引用
連携本「スマホで持ち運べる問題集」シリーズでは、さらに詳しく”問題の攻略法”を解説しています。
【おすすめする理由】
気になったときに手軽に演習できます。
間違った問題の類似問題を演習できるので、市販の問題集と併用すると便利です。
いかがでしょうか。
「確率」は数学が苦手な人も得意にしやすい分野です。
解き方は常に同じで、問題のパターンもとても少ないです。
記事内で紹介した解答手順と問題パターンを覚えてしまえば、定期テストでも高校入試でもすぐに得点源にできます。
※関連記事：高校受験によく出る数学の文章問題
演習用に市販教材とアプリも紹介していますので、学校の提出課題にプラスして演習を重ねておきましょう。
問題集・アプリは、記事内で紹介したもの以外にこちらの記事でも紹介しています。
※関連記事：数学80点を取るためのおすすめ問題集と勉強方法
【中学生のためのＺ会の通信教育】※関連記事：中学生向けオススメの通信教育5社を比較
※関連記事：中学生はいつから塾に通う？費用は？
This website uses cookies.