「比例・反比例のグラフの書き方が分からない」
「問題文から式をどうやって立てればいいか分からない」
このような悩みを感じている中学生は多いのではないでしょうか。
比例・反比例は、計算・文章題・グラフと問題の種類がたくさんあるため、こんがらがってしまいます。
ですが、コツさえつかめば比例・反比例はかなり得点しやすい単元です。
そこで、中学生向けに比例・反比例の解き方のコツを紹介します。練習問題も載せていますので、しっかり演習して比例・反比例を得意にしてしまいましょう!
※関連記事:平面図形・空間図形の解き方
※関連記事:確率の解き方
※関連記事:高校受験によく出る数学の文章問題
【下記は難関高校受験に強いZ会のHPへのリンクです。リンク先で資料請求ができます。】
Z会 中学生コースの案内
※Z会について下記記事でくわしく紹介しています。
【中学生向け】Z会タブレットコースの進め方:成績上位を取って難関校に合格する方法を解説
比例とは
まず、比例とは何なのかを確認します。
2倍、3倍に増えていく関係性
比例とは、「一方の数字が2倍、3倍になればもう一方の数字も2倍、3倍に増えていく関係性」を指します。
例えば、1個100円のリンゴを2個買うと代金は200円になります。3個買うと代金は300円になります。
表にすると↓です。
| リンゴの個数 | 1個 | 2個 | 3個 | 4個 |
| リンゴの代金 | 100円 | 200円 | 300円 | 400円 |
リンゴの個数を2倍、3倍にするとリンゴの代金も2倍、3倍に増えていくので、「リンゴの個数とリンゴの代金は比例している」と言います。
y=axと表す
比例はy=axという式で表します。このとき、「yがxに比例する」という言い方をします。
前述の1個100円のリンゴを例にして、リンゴの個数をx、リンゴの代金をyとすると以下のような式になります。
y=100x
リンゴを25個買った場合に代金がいくらになるか?を求めるには、x=25をy=100xの式に代入します。
y=100×25
y=2500
つまり、「リンゴの代金は2500円になる」というわけです。
aは比例定数
y=axの「a」は「比例定数」と呼びます。
比例定数とは、xが2倍になるとyが何倍になるかを示しています。
例えば、
y=2xなら、xが2倍になるとyも2倍になり、
y=3xなら、xが3倍になるとyも3倍になります。
比例のグラフの書き方
比例にはグラフがあります。
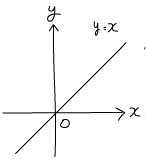
グラフを書くには、「2つの点の座標」を求めます。座標というのは、上記のような座標面での「位置」を指します。「xがいくらのときにyがいくらなのかの組み合わせ」と覚えておきましょう。
2つの点の座標が分かれば、その2点に定規をあててまっすぐ線を引きます。これでグラフは完了です。
なお、比例のグラフは「原点(0, 0)」を通るので、座標を求めるのは1つの点だけでも十分です。ただ、問題によっては原点がグラフにない場合もあるので、「2点の座標」を求めると覚えておくほうが確実です。
座標の求め方
座標を求めるには、xに数字を入れてその数字をy=axに代入するだけです。
ただし、xもyも「整数」になる数字が良いです。整数でないと、座標面でどこに点を打てば良いか分かりにくいからです。
以下のように任意のxの値をy=axの式に代入します。
例えば、y=3xなら、x=-1、x=1を代入します。y=3xにx=-1を代入するとy=-1になり、x=1を代入するとy=3になります。
これで、(-1, -3)と(1, 3)の2つの座標が分かります。
y=1/2xなら、x=-2、x=2を代入します。y=1/2xにx=-2を代入するとy=-1になり、x=2を代入するとy=2になります。
これで、(-2, -1)と(2, 2)の2つの座標が分かります。
反比例とは
つづいて、反比例とは何かを確認しましょう。
1/2倍、1/3倍に増えていく関係性
反比例は「比例の逆」です。「一方の数字が2倍、3倍になるともう一方の数字は1/2倍、1/3倍」になります。つまり、数字が減っていくわけです。
例えばリンゴ100個を何人かで分けるとします。1人でもらうと「1人あたり100個」もらえますが、2人で分けると「1人あたり50個」になります。人数が2倍になると、もらえるリンゴの数が1/2倍(=半分)になります。
表にすると↓です。
| 人数 | 1人 | 2人 | 4人 | 5人 |
| 1人あたりのリンゴの数 | 100個 | 50個 | 25個 | 20個 |
y=a/xと表す
反比例も式で表すことができます。以下のような式です。
y=a/x
前述の「100個のリンゴを分ける例」を式にすると、以下のような式になります。
y=100/x
100個のリンゴを25人で分けたら1人あたりいくつもらえるか?を求めるとすると、x=25をy=100/xに代入します。
y=100/25
y=4
つまり、1人あたり4個のリンゴをもらえるということが分かります。
反比例のグラフの書き方
反比例のグラフは曲線です。

直線なら2点を結べば良いだけですが、曲線だとそうもいきません。反比例のグラフの書き方を説明します。
座標を4つ求める
反比例のグラフでは、座標を4つ求めましょう。正確に4つである必要はありませんが、4つくらい求められれば書きやすいです。
なお、反比例のグラフは原点(0, 0)を通りませんし、x軸・y軸にも接しないように気をつけましょう。
定期テストでは、x軸に思わずグラフがくっついてしまうと「×」をつけられます。
座標の求め方
反比例のグラフではy=a/xの式にxの値を4種類代入します。
ポイントは、「xもyも整数になるようなxにすること」です。分子と同じかそれより小さい数字で、分子の約数が良いです。
y=2/xやy=-2/xの式ならxを1か2にすると良いです。y=15/xなら、xを1か3か5か15にすると良いです。
比例と反比例の違い
比例と反比例は中1で同時期に習います。どちらもグラフが出てきますし、違いが分かりにくいという中学生も多いです。
比例は増える、反比例は減る
前述のように、比例は「2倍、3倍」になり、反比例は「1/2倍、1/3倍」になります。
つまり、比例は「増えていく」、反比例は「減っていく」という違いがあります。
比例のグラフは直線で、反比例のグラフは双曲線
比例と反比例は数字の変化の仕方が異なるため、グラフも異なります。
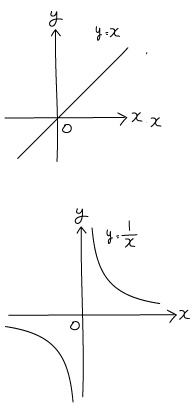
上が比例のグラフで、下が反比例のグラフです。比例は右肩上がりか右肩下がりの直線のグラフで、反比例は1つの式でご覧のように2つの曲線のグラフ(=双曲線)になります。
比例/反比例しているかどうかの見分け方
大まかに伝えると、比例は増える、反比例は減るという数値変化です。ただし、「増えれば比例」「減れば反比例」とは限りません。
見分け方を説明します。
2倍、3倍や1/2倍、1/3倍にならないと比例でも反比例でもない
比例も反比例も「一方の数字の変化に合わせて」、もう一方の数字が変化しないといけません。なおかつ、一方の数字が2倍、3倍となればもう一方の数字は、比例なら2倍、3倍…、反比例なら1/2倍、1/3倍…のように変化する必要があります。
例えば、身長が増えれば体重も増えるのが普通です。では身長150cmで体重50kgの人が身長が1.2倍の180cmになると、体重も1.2倍の60kgに増えるでしょうか。
60kgになる人もいるでしょうが、70kgになる人や80kgになる人、100kgになる人もいるでしょう。増えるとしても、「増え方」がきれいに「〇倍」とはなりません。つまり、「身長と体重は比例している」とは言えません。
このように、一方の数字を2倍、3倍にしてもう一方の数字の変化の仕方を考えます。2倍、3倍になったら「比例」で、1/2倍、1/3倍になったら「反比例」です。それ以外は「比例でも反比例でもない数字」です。
比例・反比例の解き方
では、比例・反比例の問題の解き方を説明します。
比例の式、反比例の式をつくる
まず、比例の問題なら比例の式、反比例の問題なら反比例の式をつくりましょう。
比例の式:y=ax
反比例の式:y=a/x
※aは比例定数
特に文章問題では、「式をつくりましょう」と問題文で指示されていなくてもつくるほうが良いです。大抵の問題では式をつくってその式にxやyの値を代入して答えを求めます。
グラフを描く
比例・反比例はグラフを描くと状況がイメージしやすくなります。
前述のように比例は直線、反比例は双曲線です。
基礎固めをしっかり行う
比例・反比例の問題は種類がたくさんあります。比例/反比例の式をつくる、グラフを書く、グラフから式を求める、文章題など。
解き方を考えないと思いだせない状態だと、応用問題ではややこしくなってしまいます。
基礎的な問題を繰り返し解いて、基本問題ならスラスラ解ける!というくらいにまで基本を定着させておきましょう。
比例・反比例の練習問題
それでは、比例・反比例の問題を解いてみましょう。
問題(1)
次のア~オについて、xとyが比例の関係になっているものをすべて選んでください。
ア:身長xcmの人の体重ykg
イ:1個60円のジャガイモx個と値段y円
ウ:気温x℃とアイスクリームの消費量ykg
エ:時速50kmでx時間進んだときの距離ykm
オ:200ページの本をxページ読んだときの残りyページ
解答
答え:エ
xが2倍、3倍に増えたときにyも2倍、3倍に増えるかどうかで判断します。
問題(2)
次の表をみて、xとyの関係を式で表してください。
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | -6 | -4 | -2 | 0 | 2 | 4 | 6 |
解答
答え:y=2x
y=axの式をつくり、x=1、y=2を代入します。xとyの組み合わせは表のなかで縦の列になっているものならどれでもOKです。x-3、y=6でも同じ結果になります。
問題(3)
次の表をみて、xとyの関係を式で表してください。
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | -9 | -6 | -3 | 0 | 3 | 6 | 9 |
解答
答え:y=3x
問題(2)と同じく、y=axの式をつくって表のなかのxとyの値を代入します。
問題(4)
yはxに比例していて、x=3のとき、y=-6です。xとyの関係を式で表してください。
解答
答え:y=-2x
y=axの式をつくり、x=-3、y=6を代入します。
問題(5)
yはxに比例していて、x=-2のとき、y=8です。xとyの関係を式で表してください。
解答
答え:y=-4x
y=axの式をつくり、x=-2、y=8を代入します。
問題(6)
yはxに反比例していて、x=2のとき、y=4です。xとyの関係を式で表してください。
解答
答え:y=8/x
y=a/xの式をつくり、x=2、y=4を代入します。
問題(7)
yはxに反比例していて、x=-3のとき、y=2です。xとyの関係を式で表してください。
解答
答え:y=-6/x
y=a/xの式をつくり、x=-3、y=2を代入します。
問題(8)
y=2xで、x=3のときのyの値を求めてください。
解答
答え:y=6
y=2xの式にx=3を代入します。
問題(9)
y=-4xで、y=8のときのxの値を求めてください。
解答
答え:x=-2
y=-4xの式にy=8を代入します。
問題(10)
y=2/xで、x=4のときのyの値を求めてください。
解答
答え:1/2
y=2/xの式にx=4を代入します。
問題(11)
y=-6/xで、y=3のときのxの値を求めてください。
解答
答え:x=-2
y=-6/xの式にy=3を代入します。
問題(12)
古新聞の束がある。重さをはかると1束5kgだった。
①yをxの式で表してください。
②この束が10束あると、合計何kgになりますか。
③古新聞を100kgにするには何束あれば良いですか。
解答
答え①:y=5x
古新聞の束の数をx、古新聞の重さをyとしてy=axの式をつくります。
1束5kgなので、y=axにx=1、y=5を代入します。
答え②:50kg
y=5xの式にx=10を代入します。
答え③:20束
y=5xの式にy=100を代入します。
問題(13)
1回200円でスーパーボールを1つのコップにできるだけたくさん入れるゲームがあります。コップに入れた分はすべて持って帰って良いというルールです。コップ1つのなかに入るスーパーボールの数をx、スーパーボール1個あたりの値段をy円として、以下の問いに答えてください。
①yをxの式で表してください。
②1回ゲームをしたところ、スーパーボール1個あたり20円でした。スーパーボールを何個コップに入れられましたか。
③1回ゲームをしてスーパーボール1個あたりの値段を8円以下にするには、コップのなかに何個以上のスーパーボールを入れれば良いですか。
解答
答え①:y=200/x
y=a/xの式をつくり、xとyの関係を表す表をつくります。
| x(個) | 1 | 2 | 4 |
| y(円) | 200 | 100 | 50 |
もしコップのなかにスーパーボールを1個入れると1個あたり200円になるので、x=1、y=200を代入します。
答え②:10円
y=200/xの式にx=20を代入します。
答え③:25個以上
y=200/xの式にy=8を代入します。
問題(14)
80Lの水が入る空の水そうに、毎分xLの割合で水を入れるとy分で水そうはいっぱいになりました。このとき、以下の問いに答えてください。
①yをxの式で表してください。
②この水そうを10分でいっぱいにするには、毎分何Lの水を入れるといいですか。
③この水そうに毎分10Lずつ水を入れる、何分でいっぱいになりますか。
解答
答え①:y=80/x
y=a/xの式をつくり、xとyの関係を表す表をつくります。
| x(L) | 1 | 2 | 4 |
| y(分) | 80 | 40 | 20 |
x=1のときy=80になるので、y=a/xの式にx=1、y=80を代入します。
答え②:8L
y=80/xの式にy=10を代入します。
答え③:8分
y=80/xの式にx=10を代入します。
問題(15)
1辺の長さが8cmの正方形ABCDがあります。点Pは頂点Bを出発して秒速2cmの速さで頂点Cに移動して止まります。点Pが頂点Bを出発してからx秒後の三角形ABPの面積をycm2とするとき、次の問いに答えてください。
①yをxの式で表してください。
②xとyの変域を求めてください。
③三角形ABPの面積が24cm2になるのは、点Pが頂点Bを出発してから何秒後ですか。
解答
答え:y=8x
y=axの式をつくり、xとyの関係を表す表をつくります。
| x(秒) | 1 | 2 | 3 |
| y(cm2) | 8 | 16 | 24 |
x=1のときy=8になるので、y=axの式にx=1、y=8を代入します。
答え②:0≦x≦4、0≦y≦32
点Pは頂点Bから頂点Cまで8cm移動して止まります。1秒で2cmずつ進むので出発してから4秒後には頂点Cに止まります。
xの最大値が4と分かったので、x=4をy=8xの式に代入します。
答え③:3秒後
y=8xの式にy=24を代入します。
中学数学の問題集
最後に、中学数学のおすすめ問題集を紹介します。いずれもAmazonのリンクをつけています。
『中学10分間復習ドリル 数学2年』
数学を基本からコツコツ復習したい人に向いているドリルです。
1日10分から基本問題の演習ができます。

中学10分間復習ドリル 数学2年:サクサク基礎トレ! (受験研究社)
出版社:増進堂・受験研究社
『中学2年 数学 標準問題集』
基本レベルから応用レベルまで幅広く演習できる問題集です。
定期テストで平均点前後からスタートして90点くらいまでを目指せます。

中学2年 数学 標準問題集: 中学生向け問題集/定期テスト対策や高校入試の基礎固めに最適! (受験研究社)
出版社:増進堂・受験研究社
まとめ
いかがでしょうか。
中学生向けに比例と反比例を基礎から分かりやすく解説し、問題の解き方を説明しました。
比例と反比例の公式のつくりかた、グラフのかきかた、座標の求め方を解説しています。また、比例・反比例は公式をまずつくり、xとyに数字を代入して比例定数aを求めます。
比例・反比例を早く定着できるように練習問題も15問載せているので、ぜひ解いて練習してみてください!
※関連記事:高校受験によく出る数学の文章問題
【下記は難関高校受験に強いZ会のHPへのリンクです。リンク先で資料請求ができます。】
Z会 中学生コースの案内
※Z会について下記記事でくわしく紹介しています。
【中学生向け】Z会タブレットコースの進め方:成績上位を取って難関校に合格する方法を解説


コメント