中1の正負の数の利用では、魔方陣や平均を使う問題など応用問題がたくさん出てきます。
小学校の算数にくらべて急激に難易度があがるため、戸惑う人も多いです。
そこで、正負の数の利用について、魔方陣や平均などの応用問題の解き方を解説し、練習用に問題を用意しました。
正負の数を得意にして、定期テストで高得点をねらいましょう!
正負の数の計算の仕方:加減乗除のやり方
利用の問題解説に入る前に、正負の数の計算の仕方をおさらいします。
なお、正負の数の計算方法の解説や練習問題を以下の記事でくわしく解説しています。
正負の数の計算(加法・減法・乗法・除法)
加法(足し算)のやり方
正の数や負の数を足すときは、通常通り数を加算します。正の数と負の数の組み合わせを足す場合は、大きい数から小さい数を引き、答えは大きい数の符号になります。
例: 3+(−5)=3−5=−2
減法(引き算)のやり方
正の数から負の数を引くときは、以下のルールに沿って符号を正か負にそろえます。
例: 3−(−2)=3+2=53 – (-2) = 3 + 2 = 53−(−2)=3+2=5
乗法(かけ算)のやり方
正と正、負と負の数をかけると正の数になり、正と負の数をかけると負の数になります。
例: (−3)×(−2)=6
除法(割り算)のやり方
かけ算と同じルールで、正と正、負と負は正、正と負は負の答えになります。
例:(−4)÷(−2)=2
正負の数の利用の解き方

正負の数の利用では文章問題や魔法陣の問題が良く出てきます。
解き方を問題の種類別に説明します。
正負の数の利用:魔方陣の問題の解き方
魔方陣とは、「縦、横、斜めのどの列の数字を足しても、それぞれの和が等しくなる表」です。
魔方陣を使った穴埋め問題がテストによく出てきます。以下の例題を使って、解き方を説明します。
【例題】以下の表は、縦、横、斜めの3つの数字を加えると、それぞれの和が等しくなるように数字が配置されています。表のア~エに当てはまる数字を求めてください。
| 3 | ウ | イ |
| -2 | 0 | エ |
| ア | 4 | -3 |
どこか1列の数字の和を求める
魔方陣の問題では空欄のマスがいくつもあります。ですが、数字がすべて埋まっている列が1つはあるはずです。まず、その列の数字を足して「1列の和」を求めます。
前述の表では、左上から右下までの1列がそろっています。
| 3 | ウ | イ |
| -2 | 0 | エ |
| ア | 4 | -3 |
3+0+(-3)=0
1列の数字の和が0と分かりました。
空欄が1つだけの列の数字を求める
つづいて、1列のなかで1マスだけ空欄になっている列を探します。すると、左端の縦の列、真ん中の横の列、一番下の横の列がいずれも2つの数字が分かっている状態です。
このどれかの列を足して0になるようにします。
| 3 | ウ | イ |
| -2 | 0 | エ |
| ア | 4 | -3 |
どの列で計算しても大丈夫ですが、ここでは左端の列を使ってみます。
0-3-(-2)=-1
これでアに入る数字が-1だと分かりました。
ウ、エも同様に計算してみましょう。
ウ:0-0-4=-4
エ:0-(-2)-0=+2
エが-4、エが+2だと分かりました。
| 3 | -4 | イ |
| -2 | 0 | +2 |
| -1 | 4 | -3 |
最後に残ったイも計算してみましょう。
0-3-(-4)=1
式を書いて計算間違いに気をつける
このように、魔方陣の問題では「和が分かる列を探す」ことから答えを求めていきます。
計算して求めた数字を次のマスの数字を求めるのに使うため、「どれか1つでも計算を間違うと総崩れ」になります。
暗算で答えを出してしまわずに、式を書いて計算するようにしましょう。
正負の数の利用:平均を求める問題の解き方
正負の数の利用では、平均を使う文章問題もよく出てきます。
平均の問題は解き方がすべて同じなので、コツさえつかめば得点源にできます。
以下の例題を使って解き方を説明します。
【例題】以下の表は5人の生徒A、B、C、D、Eの数学のテストの得点について、Aを基準にして表したものです。Aより高いときは正の数、低いときは負の数で表しています。
| A | B | C | D | E | |
| Aの得点との差(点) | 0 | +4 | -2 | -8 | +11 |
①5人のなかで一番得点が高い人は誰ですか。
②BとDの得点のちがいは何点ですか。
③Aの得点が80点のとき、この5人の得点の平均は何点ですか。
表の見方を知る
正負の数の利用で平均の問題では、「基準との差(ちがい)」を使います。
例題では、Aの得点を基準にしてB・C・D・Eの得点を表しています。
表をみるとBは+4となっています。つまり、「BはAより4点高い」という意味です。
①の問題では、「5人のなかで一番得点の高い人は誰ですか」と問われています。Aを基準にしているので、+の点数が書かれている人はAよりも高い点数を取っています。
Bが+4、Eが+10です。Eのほうが高いので、5人のなかで一番得点の高い人はEです。
2つの数のちがいを引き算で求める
つづいては、BとDの得点のちがいを求める問題です。
ちがいを求めるには、それぞれの数字を引き算します。
BとDとの違いなので、(Dの得点)-(Bの得点)か(Bの得点)-(Dの得点)をします。
-8-(+4)=-12
数字を絶対値にする
BとDを引き算したら-12でした。この数字を絶対値にします。
絶対値は「符号を取った数字」なので、-12の絶対値は12です。
これで、BとDの点数差は12点だと分かりました。
全員の平均を求める
全員の平均を求める問題もよく出てきます。2通りの解き方があります。
基準との差から平均を求める
1つ目は、基準との差を使って求める方法です。こちらの方法が一般的で、計算が少なく済みます。
| A | B | C | D | E | |
| Aの得点との差(点) | 0 | +4 | -2 | -8 | +11 |
上記の表にある「Aの得点との差」をすべて足し算します。
0+(+4)+(-2)+(-8)+(+11)
=+5
この計算で出てきた「5点」は「Aの得点+5点」という意味です。
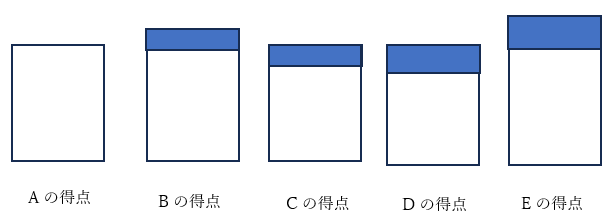
上記の白枠部分がAの得点で、青枠部分がAの得点とのちがいです。青枠部分をすべて足すと5点になります。
5人合わせて5点なので、1人当たり(=平均)は
5点÷5人=1点
つまり、5人の平均得点は(Aの得点)+(1点)=81点になります。
合計から平均を求める
もう1つの方法はもっとオーソドックスな求め方で、合計から平均を求めるやり方です。小学校で習った平均と同じ方法です。
前述のような「Aの得点とのちがいに注目する方法」がピンとこない人は、こちらの方法で解くほうがテストで解きやすいです。
まず例題にある5人の得点を求めます。
| A | B | C | D | E | |
| Aの得点との差(点) | 0 | +4 | -2 | -8 | +11 |
上記表は「Aの得点との差」です。これをもとに5人それぞれの得点を求めます。
Aが80点なので、Bは80+(+4)=84点というように、足し算していきます。すると、以下の表のようになります。
| A | B | C | D | E | 合計 | |
| 得点(点) | 80 | 84 | 78 | 72 | 91 | 405 |
5人全員の合計得点が405点と分かったので、
405点÷5人=81点
平均は81点になります。
この方法のほうが計算は多くなりますが、考え方はシンプルです。
正負の数の利用の解き方のQ&A
Q1: 平均を求めるときの正負の数の使い方は?
A: 数の合計をその数の個数で割って平均を求めます。正負の数が混ざっている場合でも、同じルールを適用します。
例: 点数が −2,5,3の3つなら、
合計(−2+5+3=6)を3で割り、平均は 6÷3=2です。
Q2: 魔方陣で正負の数を使う問題はどう解きますか?
A: 魔方陣は縦・横・斜めの合計が同じになる配置を見つけます。正負の数が含まれる場合、合計を考慮しつつ配置する必要があります。
例: 合計が0になるよう配置する場合、−1,2,−1-1, 2, -1−1,2,−1 などを組み合わせます。
Q3: 個数を求める問題で正負の数はどう使う?
A: 必要な個数に正負の数を使うとき、合計が目標数になるまで正負の数を加えたり引いたりして調整します。
例: 10個を目指す場合、正負の数で「±10」などの目標に調整することができます。
Q4: テストの点数を求める問題で正負の数をどう扱う?
A: テストの点数が増減する問題では、点数を増加ならプラス、減点ならマイナスとして計算します。
例: 基準となる点数が 50 点で、追加点数 +10点、減点 −5点がある場合、最終点数は
50+10−5=55点になります。
正負の数の利用の問題
それでは、正負の数の利用の練習問題を解いてみましょう。
問題(1)
A、B、C、D、Eの5人でゲームをしました。5人の合計得点が3点のとき、以下の問題に答えてください。
①Aが3点、Bが-2点、Cが4点、Dが-4点のとき、Eの得点を求めてください。
②Aが-4点、Bが-2点、C・D・Eが同じ得点のとき、Cの得点を求めてください。
③A・Bの得点の平均が9点のとき、C・D・Eの得点の平均を求めてください。
解答
①2点
5人の得点の合計が3点なので、A~Dの4人の得点を引いてEの得点を求めます。
3-3-(-2)-4-(-4)
=2
②3点
AとBの得点の合計を求め、5人の得点の合計からC・D・Eの得点の合計を求めます。
AとB:-4+(-2)=-6
5人の合計:3点
C・D・Eの合計:(5人の合計)-(AとBの合計)=9
C・D・E3人合わせて9点で、3人とも同じ得点なので、
9÷3=3
これで、C・D・Eは1人3点ずつだったと分かります。
③-5
A・Bの合計得点を求め、その得点からC・D・Eの合計得点→平均得点を求めます。
A・Bの合計:9(点)×2(人)=18(点)
5人の合計得点からA・Bの合計得点を引いて、C・D・Eの合計得点を求めます。
3-18=-15
3人の合計が-15点なので、平均点は以下のとおり。
-15÷3=-5
問題(2)
以下の表は、縦、横、斜めの3つの数字を加えると、それぞれの和が等しくなるように数字が配置されています。表のア~オに当てはまる数字を求めてください。
①
| ウ | -3 | ア |
| エ | 1 | オ |
| 0 | 5 | イ |
②
| ア | ウ | -3 |
| -4 | 0 | イ |
| 3 | エ | オ |
③
| -5 | 0 | -1 |
| エ | イ | -6 |
| オ | ウ | ア |
解答
①
| 4 | -3 | 2 |
| -1 | 1 | 3 |
| 0 | 5 | -2 |
真ん中の縦の列より、1列の合計は3になります。
| ウ | -3 | ア |
| エ | 1 | オ |
| 0 | 5 | イ |
次に、1列のなかで1マスだけ分からない列を探し、
「右斜めの列」と「一番下の横の列」のアとイを計算で求めます。
| ウ | -3 | ア |
| エ | 1 | オ |
| 0 | 5 | イ |
ア:3-1-0=2
イ:3-0-5=-2
これでほかの列も計算で求められるようになります。
| ウ | -3 | 2 |
| エ | 1 | オ |
| 0 | 5 | -2 |
②
| 1 | 2 | -3 |
| -4 | 0 | 4 |
| 3 | -2 | -1 |
右斜めの列の数字を合計すると、1列の和は0だと分かります。
| ア | ウ | -3 |
| -4 | 0 | イ |
| 3 | エ | オ |
次に、1列のなかで1マスだけ分からない列を探し、
「左はしの縦の列」と「真ん中横の列」のアとイを計算で求めます。
| ア | ウ | -3 |
| -4 | 0 | イ |
| 3 | エ | オ |
ア:0-(-4)-3=1
イ:0-(-4)-0=4
これでほかの列も計算で求められるようになります。
| 1 | ウ | -3 |
| -4 | 0 | 4 |
| 3 | エ | オ |
③
| -5 | 0 | -1 |
| 2 | -2 | -6 |
| -3 | -4 | 1 |
一番上の横の列の数字を合計すると、1列の和は-6だと分かります。
| -5 | 0 | -1 |
| エ | イ | -6 |
| オ | ウ | ア |
次に、1列のなかで1マスだけ分からない列を探し、
「右はしの縦の列」のアを計算で求めます。
| -5 | 0 | -1 |
| エ | イ | -6 |
| オ | ウ | ア |
-6-(-1)-(-6)=+1
アが+1と分かったので、つづいてイを求めます。
| -5 | 0 | -1 |
| エ | イ | -6 |
| オ | ウ | 1 |
-6-(-5)-1=-2
イが-2と分かると、ウ・エ・オも計算して求められるようになります。
問題(3)
aを正の数、bを負の数とします。次の計算結果が正の数になる場合は+、負の数になる場合は-を書いてください。
①-a
②a×b
③b2
④(-b) 2
⑤a-b
⑥(b-a)÷a
⑦a×b-a÷b2
解答
①-
②-
③+
bを(-3)とすると、b2は(-3) 2になります。
(-3)×(-3)なので、+です。
④+
bを(-3)とすると、(-b) 2は{-(-3)} 2になります。つまり、+3を2乗しているので、答えは+です。
⑤+
⑥-
aを3、bを-3とすると、
(-3-3)÷3=-2
⑦-
aを3、bを-3とすると、
3×(-3)-3÷(-3)2
=-9-1/3
=-28/3
a×bが-になり、
-a÷b2も-になるので、abの数字がいくらであっても答えは-になります。
問題(4)
A、B、C、D、E、Fの6人の生徒が英語のテストを受けました。以下の表は6人の得点を表したものです。Bの得点を基準にして、Bより高いときは正の数、低いときは負の数で表しています。
| A | B | C | D | E | F | |
| Bの得との差(点) | -4 | 0 | +5 | +8 | -15 | +12 |
①一番得点の高い人は誰ですか。
②AとEの得点差は何点ですか。
③Bが80点のとき、6人の得点の平均を求めてください。
解答
①F
②11点
Aが-4点で、Eが-15点。この2つの数字を引き算します。
-15-(-4)=-11
-11を絶対値にして11点がAとEのちがいです。
③81点
A~Fまで6人の合計を、Bを基準にして求めます。
-4+0+(+5)+(+8)+(-15)+(+12)
=6
6点を6人で割って、Bの得点より平均1点上だと分かりました。
Bの得点は80点なので、6人の平均得点は81点です。
問題(5)
Aさんが国語のテストを1年間に5回受ける予定で、これまで4回受けました。目標点を80点として、これまで受けた点数と80点との差を以下の表に表しています。5回のテストの平均点を80点以上にするには、5回目のテストで何点取れば良いですか。
| 1回目 | 2回目 | 3回目 | 4回目 | 5回目 | |
| 目標点との差(点) | -12 | -3 | +2 | +6 |
解答
答え:87点
解説:
4回目までの得点を、80点を基準にして求めます。
-12+(-3)+(+2)+(+6)=-7
平均80点にするには、4回目までで7点足りないと分かりました。つまり、5回目で80点より7点多くとれば5回の平均が80点にのります。
問題(6)
あるお店では一日に来店するお客の目標人数を50人にしています。ある週の火曜日から日曜日までの6日間の来店人数を、50人を基準にしてそれより多い場合を正の数、少ない場合を負の数で以下の表に表しています。
| 火曜日 | 水曜日 | 木曜日 | 金曜日 | 土曜日 | 日曜日 | |
| 目標人数との差(人) | -12 | -10 | -15 | +5 | +18 | +20 |
①お客の人数が最も多い日と最も少ない日で何人ちがいがありますか。
②6日間の客の人数の平均を求めてください。
解答
①35人
最も多い日が+20の日曜日、
最も少ない日が-15の木曜日です。
+20-(-15)=35
②51人
50人を基準にして6日間のお客の合計人数を求めます。
-12+(-10)+(-15)+(+5)+(+18)+(+20)
=+6
6人を6日間で割って、1日あたり(=平均)1人多いと分かります。
50+1=51人

中学数学の問題集
最後に、中学数学のおすすめ問題集を紹介します。
【中学生のためのZ会の通信教育】『中学10分間復習ドリル 数学2年』
数学を基本からコツコツ復習したい人に向いているドリルです。
1日10分から基本問題の演習ができます。

中学10分間復習ドリル 数学1年:サクサク基礎トレ! (受験研究社)
出版社:増進堂・受験研究社
『中学1年 数学 標準問題集』
基本レベルから応用レベルまで幅広く演習できる問題集です。
定期テストで平均点前後からスタートして90点くらいまでを目指せます。

中学1年 数学 標準問題集: 中学生向け問題集/定期テスト対策や高校入試の基礎固めに最適! (受験研究社)
出版社:増進堂・受験研究社
まとめ
いかがでしょうか。
中1向けに正負の数の利用の解き方と練習問題を用意しました。
正負の数では平均の文章問題や魔方陣の問題が良く出てきます。苦手に感じる子も多いですが、問題パターンは毎回同じです。コツをつかんでしまえば応用問題でも正解しやすくなります。
数学の問題集を使うなどして演習を重ねましょう!
※関連記事:【中学生】Z会タブレットコースの進め方:成績上位を取って難関校に合格する方法や費用を解説
【中学生のためのZ会の通信教育】


コメント