「中学校に入って数学で苦労している」
「正負の数の計算方法がたくさんあってややこしい」
このような声を中1の人たちから聞くことが多いです。
たしかに、小学校までの算数にはなかった計算方法も出てくるため、ややこしくなります。
ですが、正負の数は中学数学の一番の土台であり、「しっかりと」解けるようになっておきたい単元です。
そこで、中学生向けに正負の数の計算方法を解説し、練習のための計算問題を用意しました。加法・減法・乗法・除法の計算ルールや四則計算、間違いがちな累乗の計算の仕方も解説しています。ぜひ正負の数を得意にしましょう!
※関連記事:中1最初のテスト:初めての中間テスト範囲はどこで、勉強をいつからどうやってすれば良いか紹介します
正負の数とは

中学に入ると、「正負の数」が登場します。小学校の算数から発展して、プラス・マイナスがでてきます。
まず、正の数・負の数・自然数の3種類を覚えておきましょう。
正の数は「0より大きい数」
正の数とは、「0より大きい数字」のことです。
+3、+2.5、+1/3のように、整数、分数、小数いずれの場合もあります。
「+3」だと「プラス3」と読みます。
負の数は「0より小さい数字」
負の数とは、「0より小さい数字」のことです。
-3、-2.5、-1/3のように、整数、分数、小数いずれの場合もあります。
「-3」だと「マイナス3」と読みます。
自然数は「正の整数」
自然数とは「正の整数」です。正の数は0より大きい数字で、整数・分数・小数があります。
自然数は0より大きい数字のなかで整数だけを指します。
+3、+4、+5などのプラスの整数だけです。
正の数・負の数・自然数の違い
正の数、負の数の自然数の違いをまとめておきます。
自然数は正の数の一部で、プラスになる整数を指します。
| 正の数 | 0より大きい数 | +3、+2.5、+1/3など | |
| 自然数 | 0より大きい整数 | +3、+4、+5など | |
| 負の数 | 0より小さい数 | -3、-2.5、-1/3など | |
絶対値とは
正の数・負の数・自然数以外に、「絶対値」を覚えておきましょう。
絶対値とは「原点からの距離」を指します。大まかに言うと、「符号を取った数字」です。
例えば+4の絶対値は4で、-7の絶対値は7です。
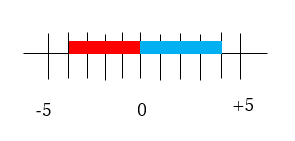
数直線をイメージしてみましょう。0から+4までの距離と0から-4までの距離は同じで、+4も-4も0から4つ進んだところです。この距離が絶対値です。
正負の数の計算方法

正負の数は小学校で習った整数や小数と同じように計算ができます。
中学校では足し算・引き算・かけ算・わり算のことを加法・減法・乗法・除法と呼びます。さらに、それぞれの計算した答えを和・差・積・商と言います。
いずれの名前も憶えておきましょう。
正負の数の符号の変わり方
正負の数の計算では、符号に注意が必要です。符号というのは「+」(プラス)や「-」(マイナス)といった、「数字の前につく記号」のことです。
計算式のなかで、「++」「+-」「-+」「--」のように符号が連続することがあります。このとき、以下のように1つの符号にまとまります。
同じ種類の符号がならんだら「+」になり、
異なる符号がならぶと「-」になります。
数直線を使ってイメージしよう
「「++→+」のような書き方だと分かりづらい…」という人は、数直線を使うとイメージしやすいです。
例えば以下の数直線は「-5+3」のイメージです。「-5」からスタートして、右に3つ進んだ箇所が答えになります。
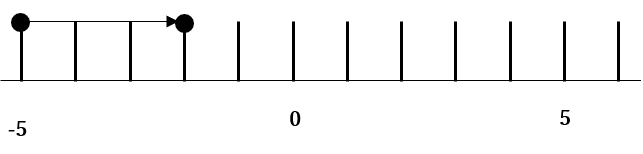
参考:ベネッセ教育情報「【正負の数】 異符号の加法の符号はなぜ絶対値大のほう?」
正負の数の加法・減法のやり方
符号の変化に注意しつつ、加法・減法のやり方を説明します。
かっこを外す
まず、加法・減法では( )がついているものは( )を外します。
例えば、(+3)+(-4)の場合、以下のように計算します。
(+3)+(-4)
=+3-4
=-1
( )を外すと、前述のように符号が2種類ならびます。上記の計算式では「+-」と、異なる符号がならんだので「-」になります。
同じ符号の数字はそのまま計算する
( )を外して同じ符号がならんだ場合、そのまま計算します。
例えば、(+4)-(-5)の場合、以下のように計算します。
(+4)-(-5)
=+4+5
=+9
異なる符号の数字は絶対値で計算する
( )を外して異なる符号がならんだ場合、絶対値を使って計算します。絶対値とは「+や-の符号を取った数字」のことです。
(+3)+(-4)の場合、( )を外すと「+3-4」という式になります。
「+3」の絶対値は「3」で、「-4」の絶対値は「4」です。絶対値を比較すると「4」のほうが大きいので、「4-3」をします。すると、「1」になりました。
さらに、「4」はもともと「-」がついているので、「1」に「-」をつけます。
つまり、「-1」が答えです。
3つ以上の数の加法・減法
(+2)-(-4)+(-3)のように、3つ以上の数の加法・減法の場合があります。
「加法だけの計算式」になおして計算しましょう。以下のようになります。
(+2)-(-4)+(-3)
=(+2)+(+4)+(-3)
「--」→「+」になり、「+-」→「-」になるというルールでした。そのため、-(-4)は+4になり、+(-3)は-3になります。
すべて加法になったので、あとは(+2)と(+4)と(-3)を足します。
(+2)と(+4)で+6になり、6-3をして、答えは+3になります。
正負の数の乗法・除法のやり方
乗法・除法も符号の変化に注意が必要です。
乗法・除法では「-3×(-4)」のように式を1つのまとまりとみなして、-がいくつあるかを数えます。
-が偶数個あれば+にする
「-3×(-4)」であれば、「-」の符号が2つあります。-が2つあるときには「+」になります。
2つだけでなく、4つ、6つのように偶数個あれば符号は「+」になります。
-が奇数個あれば-にする
-が奇数個の場合、符号は「-」になります。
例えば「+3×(-4)」の式だと、-は1つだけ。つまり奇数個です。そのため、符号は-になります。
符号と数字を組み合わせる
符号とは別に数字だけ計算し、あとで符号と数字を組み合わせます。
「+3×(-4)」の式の場合、符号は-になります。数字だけ計算すると「3×4」なので12です。
-と12を組み合わせて「-12」が答えになります。
分数をふくむ除法の計算のやり方
分数をふくむ除法の場合、小学校で習った分数のわり算と同じ計算方法を使います。
÷の後ろの数字を逆数にしてかけ算します。
3÷1/2の場合、以下のように計算します。
3×2/1=6
ここに符号が組み合わせます。例えば「(-3)÷(+1/2)」の式では、数字だけ計算すると前述のように「6」になります。
符号だけみると、-が1個なので符号は-になります。
-と6と組み合わせて、答えは「-6」です。
3つ以上の数の乗法・除法のやり方
3つ以上の数で乗法・除法をする場合もあります。その場合、乗法だけの式になおします。
「(-3)÷(+1/2)×(-2)」の式を計算してみます。÷があるので、×にかえて乗法だけにします。すると、以下のような式になります。
(-3)×(+2)×(-2)
-3と2と-2をかけ算します。符号だけみると-が2個なので+になります。数字だけ計算すると3×2×2で12になります。+と12を組み合わせて「+12」が答えです。
正負の数の四則計算の順序
ここまでは、「加法・減法」と「乗法・除法」が別々の式にある場合の計算方法を説明してきました。これらが1つの式に入っている場合もあります。
計算の仕方はこれまでどおりですが、計算する順番に注意が必要です。
1番目:かっこの中を計算する
まず、( )の中を計算します。
例えば、「(-3+4)×2+4」という計算式では「(-3+4)」、「×2」、「+4」の3つの計算があります。これらのなかで( )のついている「(-3+4)」を1番目に計算し、「1」を出しておきます。
2番目:乗法・除法をする
( )の次に計算するのは乗法・除法です。
「(-3+4)×2+4」では「×2」が2番目です。(-3+4)が1になるので、1×2で2になります。
3番目:加法・減法をする
最後には( )のついていない加法・減法をします。
「(-3+4)×2+4」の式では(-3+4)×2が2になるので、2+4をします。答えは6になります。
正負の数の累乗の計算のやり方
正負の数で多くの中1生がつまずくのが累乗の計算です。
累乗とは同じ数の積
まず、累乗の意味を確認します。累乗とは「同じ数の積」を指します。積はかけ算の答えなので、言いかえると累乗とは「同じ数を何回かかけ算すること」です。
例えば3×3は3を2回かけています。32と書き、「3の2乗」と読みます。
(-3)2と(-32)の違い
累乗でややこしいのは( )がつく累乗のときです。
例えば、(-3)2と(-32)はよく似ていますが、計算の仕方が異なります。
(-3)2は「-3×(-3)」をします。一方、(-32)は「-3×3」です。計算結果は以下のようになります。
(-3)2=-3×(-3)=9
(-32)=-3×3=-9
乗法・除法より先に累乗の計算をする
累乗の計算は乗法・除法より先にします。
例えば「(-32)×4」では、以下のようになります。
(-32)×4
=-9×4
=-36
かっこより先に累乗の計算をする
( )のついている計算式では普通、累乗から計算します。
例えば{(-4)2+32}×4の場合、以下のように計算します。
{(-4)2+32}×4
={(-4)×(-4)+32}×4
=(16+32)×4
=48×4
=192
ほとんどの正負の数の式では以下の順番です。
①累乗
②かっこ
③乗法・除法
④加法・減法
ここまでの内容を理解できた人は、さらに正負の数の利用(文章問題)にもチャレンジしてみてください。以下の記事でくわしく解説しています。
正負の数の利用:平均(文章問題)や魔方陣などの応用問題の解き方と練習問題
正負の数の計算問題【中学生向け】
ここまで説明してきた正負の数の計算方法を思い出しながら、計算問題を解いて慣れていきましょう。
計算問題が解けるようになったら、正負の数の利用(文章題)にもチャレンジしてみてください。
正負の数の利用:平均(文章問題)や魔方陣などの応用問題の解き方と練習問題

問題(1)
次の計算をしてください。
①3-7
②+5+(-4)
③-3-(-5)
④+4-(+2)
⑤-1/2+3/2
解答
①-4
②1 ※+1でも正解
③2 ※+2でも正解
④2 ※+2でも正解
⑤1 ※+1でも正解
問題(2)
次の計算をしてください。
①-4+3-(-2)
②3-(+2)+(+3)
③-0.5+2.5-(-2)
④-1/2-(+1.5)+(+3)
⑤0.4-2/5+(-3/7)
解答
①1
②4
③4
④1.3
⑤-3/7
問題(3)
次の計算をしてください。
①-2×4
②3÷(-1/2)
③-2÷(-3)×6
④1/3×1/2÷(-2)
⑤-3÷(-1/3)÷2×1/9
解答
①-8
②-6
③4
④-1/12
⑤2
2つずつ計算します。まず、-3÷(-1/3)だけ計算します。
-3÷(-1/3)
=-3×(-3)
=9
つづいて、9÷2をします。
9÷2
=9/2
最後に9/2×1/9をします。
9/2×1/9
=2
問題(4)
次の計算をしてください。
①(-2+3)×4
②3÷(-3-2)
③-2+(-3)×(1+4)
④{2×(-3+4)}-5
⑤1/2+4-{(2-4)÷1/2}
解答
①4
(-2+3)=1
1×4=4
②-3/5
-3-2=-5
3÷-5=-3/5
③-17
1+4=5
-3×5=-15
-2-15=-17
④-3
-3+4=1
2×1=2
2-5=-3
⑤7/2
2-4=-2
-2÷1/2=-1
1/2+4-1=7/2
問題(5)
次の計算をしてください。
①-32
②(-32)
③(-3)2
④22×32-(1/2) 2×42
⑤{32-2+(-3/2) 2}-(5/2) 2
解答
①-9
②-9
③9
④32
22×32
4×9
=36
(1/2) 2×42
=1/4×16
4
36-4=32
⑤3
{32-2+(-3/2) 2}-(5/2) 2
=32-2+(-3/2) 2-25/4
=9-2+9/4-25/4
3
正負の数に関するQ&A(中学生向け)
Q1: 正の数と負の数の違いは何ですか?
A1: 正の数は0より大きい数で、負の数は0より小さい数です。たとえば、+3は正の数、-5は負の数です。
Q2: 正負の数の足し算はどうやりますか?
A2: 同じ符号の数は符号をそのままにして数を足し、異なる符号の数は大きい方から小さい方を引き、符号は大きい方に合わせます。
Q3: 正負の数の引き算のやり方は?
A3: 引き算は、相手の数を逆の符号にして足し算に変えます。たとえば、3 – (-2)は3 + 2になります。
Q4: 正負の数のかけ算・割り算のルールは?
A4: 符号が同じなら答えは正、符号が違うなら答えは負になります。たとえば、-4 × -3は+12、-4 ÷ 2は-2です。
Q5: 0は正負の数に入りますか?
A5: 0は正でも負でもなく、数直線の中央にあります。
中学数学のおすすめ問題集
最後に、中学数学のおすすめ問題集を紹介します。
『中学10分間復習ドリル 数学1年』
数学を基本からコツコツ復習したい人に向いているドリルです。
1日10分から基本問題の演習ができます。

中学10分間復習ドリル 数学1年:サクサク基礎トレ! (受験研究社)
出版社:増進堂・受験研究社
『中学1年 数学 標準問題集』
基本レベルから応用レベルまで幅広く演習できる問題集です。
定期テストで平均点前後からスタートして90点くらいまでを目指せます。

中学1年 数学 標準問題集: 中学生向け問題集/定期テスト対策や高校入試の基礎固めに最適! (受験研究社)
出版社:増進堂・受験研究社
まとめ
いかがでしょうか。
中1向けに正負の数の計算の仕方を解説しました。
加法は足し算、減法は引き算、乗法はかけ算、除法はわり算のことです。プラスマイナスはもちろん、小数は分数になおしてから計算するなどの解き方も中学校に入って出てきています。
繰り返し計算問題を解いて「正確に・速く」解けるよう練習しましょう!
※関連記事:高校受験で内申点はいつからいつまで成績に入るのか:中1から9教科必要?中3だけじゃない?
※Z会について下記記事でくわしく紹介しています。
【中学生向け】Z会タブレットコースの進め方:成績上位を取って難関校に合格する方法を解説


コメント