小学校5年生は小学校で1番算数がむずかしくなる学年と言われています。
分数のかけ算・割り算は小学生が習う計算のなかでは1番難易度が高いですし、割合などの抽象的な概念を扱う単元が本格的に登場します。
しかも5年生の内容は6年生の算数や中学生の数学に直接つながっており、算数・数学が伸びるかどうかの境目になります。
ぜひここで算数に得意意識をもってほしいですね。
そこで、
を紹介します。
※関連記事：小学校5年生におすすめの算数ドリル・問題集
この記事は下記の方向けです。
※関連記事：算数が苦手な子必見！家庭でできる「算数の伸ばし方」
※関連記事：Z会小学生コースの進め方：自主性や考える力を伸ばせる問題の特徴を紹介
「小学生は学年×10分勉強しましょう」とよく言われます。
5年生だと1日50分です。
本当にこれで十分なのでしょうか。一般的に小学4年生は毎日どれくらい勉強しているものなのでしょうか。
実は、5年生は「50分」どころか1.5倍以上の「80分」勉強しています。
下記のグラフをご覧ください。小学校1年生から6年生までを対象に、1日の家庭学習時間を調査した結果です。
3年生から4年生で平均家庭学習時間は6分伸びていますが、
4年生から5年生で8分アップと、増加幅が大きくなっています。
一方で、家庭学習時間の中央値（データのちょうど真ん中）は全学年通じて60分です。
このことから、下記の状況が読み取れます。
「勉強する子」と「勉強しない子」にわかれていく学年ともいえます。
学年が上がると塾に通いはじめる子が多くなります。
下記のグラフは、学年別の1人当たりの学習費です。
ご覧のように、4年生（74,190円）から5年生（108,779円）で学習費が1.5倍近くに増加しています。
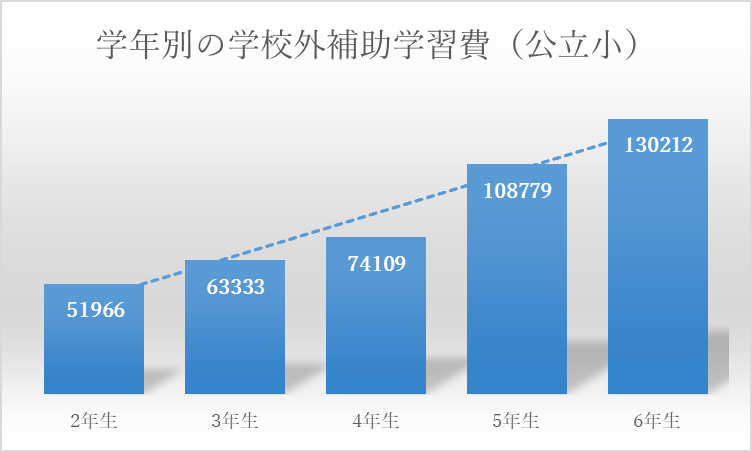
しかも5年生では45,1%が塾を利用していることもわかっています。
それまでは家庭での学習中心だった子が、塾で本格的に勉強をはじめだすのが5年生なのです。
中学受験塾でも大きな変化が見られます。
4年生までは中学受験内容の基礎固めが中心でしたが、5年生から発展的な内容に入ります。
それに伴って1週間の通塾日数も増え、
4年生では週2-3日だったのが5年生では週3-4日が当たり前になります。
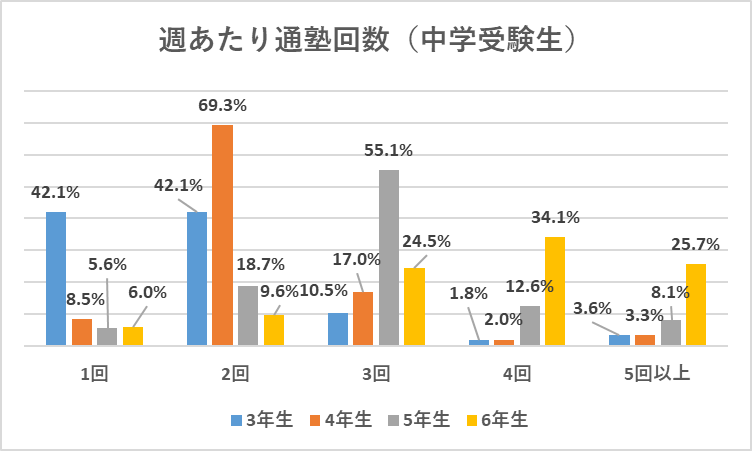
勉強量が増えて内容もむずかしくなるため、塾の模擬試験で偏差値60前後をキープしていた子が、5年生で急に50台前半に落ち込んだりすることもよくあります。
※関連記事：中学受験の算数はなぜむずかしいのか？受験算数の伸ばし方4つを紹介！
5年生の算数はどのような内容を習うのでしょうか。下記の表は5年生の単元一覧表です。
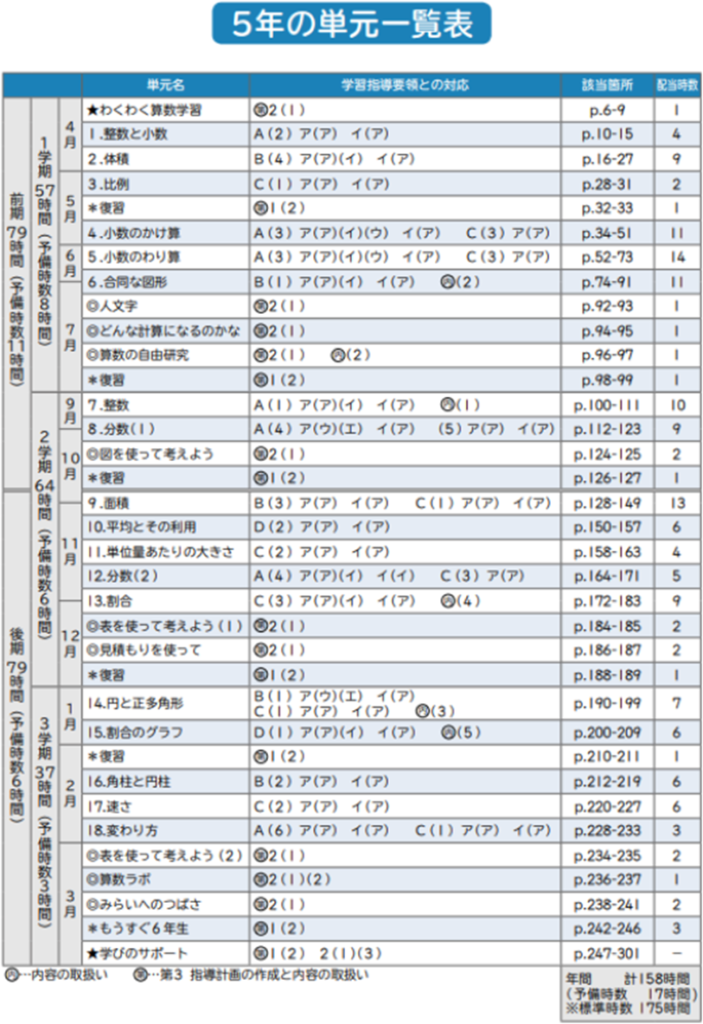
5年生の単元は、「計算」「文章問題」「図形」と多岐にわたります。
上記の単元一覧表を元に、主要単元を下記の表にまとめました。
| 学期 | 主要単元 |
| 1学期 | 「整数と小数」「体積」「比例」「小数のかけ算・わり算」「合同な図形」 |
| 2学期 | 「分数」「面積」「平均」「単位量あたり」「割合」 |
| 3学期 | 「円と正多角形」「角柱と円柱」「速さ」「変わり方」 |
5年生の算数ではとても重要な内容をいくつか習います。
5年生では通分・約分を習います。通分も約分も、分数の計算をするうえで欠かせない単元です。
通分や分数のたし算・引き算で使い、約分は分数のかけ算・わり算で使います。
5年生では約数・倍数も習います。
約数は「その数字を割り切れる数字」のことで、例えば「12の約数」は「1、2、3、4、6、12」です。
また、倍数は「その数字を2倍、3倍とかけていった数字」のことで、例えば「3の倍数」は「3、6、9、12、…」です。
応用しやすい内容なので、文章問題でよく使われます。
小学校の算数のなかでもとびぬけて苦手な子が多いのが「割合」です。3割、30%のような表し方をします。
クラスのなかでスポーツが好きな子の割合など、グラフや文章問題でよく使います。
平均や割合が分かる子は数字の性質を感覚的に理解できており、小学校だけでなく中学校でも数学を得意にしやすいです。
逆に平均や割合が分からないために、中学校の数学の半分ほど（文章題、比例・反比例、関数、データ活用など）で苦労してしまう子が多くいます。
※割合と速さの苦手克服方法は以下の記事で説明しています。中学受験をしない子も使える解き方です。
※関連記事：割合の問題の解き方
※関連記事：「比」の解き方
5年生になると、公立中高一貫の受検を決める家庭が多くなります。
適性検査は小学校で習う範囲から出題されますが、なかでもよく出てくるのが「約数・倍数」「割合」「面積」をはじめとした「5年生で習う範囲」です。
中学校の数学でもよく出てくる内容が多く、受検する子にも受検しないしない子にも重要な内容が目白押しの学年です。
※関連記事：公立中高一貫校の勉強方法
※関連記事：公立中高一貫校の適性検査対策におすすめの問題集
では5年生の算数はどのように対策すればいいのでしょうか。
大きく2つあります。
1つ目は復習を習慣化することで、2つ目は単元ごとのポイントと対策方法を知っておくことです。
筋肉食堂から宅食サービス開始！【筋肉食堂DELI】苦手が生まれる大きな原因は、習った内容が十分に定着していないことにあります。
前述のように、「分数」や「平均」があやふやなままだと「割合」は定着しにくくなります。
算数は積み重ねの教科ですから、今習っている内容をきっちり定着させると次に習う内容も定着しやすくなります。
復習をこまめに行って定着度を上げましょう。
記憶に関する有名な研究で、エビングハウスの忘却曲線というものがあります。
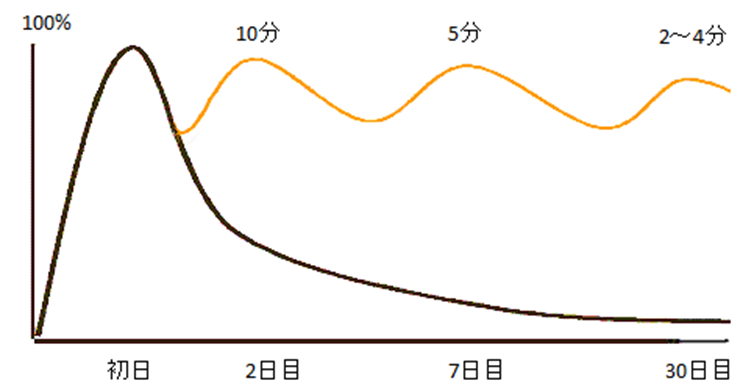
黒字の曲線は学習した内容が記憶にどれくらい定着していたかを表しています。
学習した初日を100%とすると、2日目には26%まで定着率が落ちています。3/4も忘れてしまうのです。
オレンジの曲線は、1度学習した内容を復習すると定着率がどう変わるかを示しています。
1度学習した内容を次の日に復習すると記憶が9割以上復活しています。
小学校からは毎日宿題が出ます。宿題をするときに、今日の宿題をするだけでなく、昨日の宿題をもう1度やるようにしてみましょう。
これを習慣的に行うだけで、「復習しよう！」と思わなくても毎日復習ができます。
算数の基礎力は計算です。計算が「苦手」「あまり得意ではない」状態だと、応用問題を解くのに苦労します。
毎日10分計算練習をしましょう。
5年生にもなると、子どもによって得意・苦手単元が出てきます。
苦手単元は応用問題の演習に入る前に、基本問題の演習を繰り返してみましょう。
基本問題は「正解できる」だけでなく、「スラスラ正解できる」ようにしておくのがポイントです。
ときどき計算間違いや単位の間違いをしている、問題文を読み間違えている。こうしたケアレスミスが出ている間は基本問題中心に演習するほうが伸びやすいです。
5年生では正多角形など、いろいろな図形が登場します。各図形の性質を覚えるのはもちろん、感覚的に把握しておく必要があります。
定規やコンパスを使わずに、フリーハンドで丁寧に描いてみましょう。ある程度正確に描けるようになってきたら図形の問題も解きやすくなってきます。
ここからは、単元別に算数の勉強方法を紹介します。
オーガニックの出産祝い【Haruulala】小数の計算では「かけ算・わり算では小数点の位置が変わる」と覚えておきましょう。
このポイントを理解するために、5年生では1.234のような小数を10倍、100倍、1000倍して小数点を動かす練習をします。かける数や割る数に0がいくつあるかで、小数点を動かす回数が決まります。
10倍すれば小数点が1つ右に動きます。1.234は12.34になります。100倍すれば2つ右に動くので、123.4です。
10で割るとその逆で1つ左に動くので、1.234は0.1234になります。100で割ると2つ左に動くので、0.01234になります。
| かける | 割る | |
| 10 | 1つ右に動く | 1つ左に動く |
| 100 | 2つ右に動く | 2つ左に動く |
| 1000 | 3つ右に動く | 3つ左に動く |
これを意識しながら問題を解くだけで、小数の計算はかなりスムーズに上達します。
なお、小数の計算でも「たし算・ひき算」は小数点が動きません。この違いに注意しましょう。
体積の問題では「単位」がややこしいです。cm2なのか、m2なのか。
同じ図形でも単位が変わっている問題も多く、そこで間違えてしまう子が続出します。
cm⇔mやcm2⇔m2⇔km2などいくつもの単位変換が出てきますが、cm⇔mの単位変換だけ覚えておけば大丈夫です。
1m=100cmですから、2mなら200cmになります。
このとき、m→cmにするのに「×100」をしています。2mなら、2×100をしています。
この「×100」を、m2なら2回して、m3なら3回します。
2mなら、「2×100」でした。
→ 2m2なら、「2×100×100」です。
→ 2m3なら、「2×100×100×100」です。
とても単純な仕組みなのですが、覚えておくと結構便利です。mにくっついている2と3だけ見れば良いので頭を使いません。
単位変換に慣れてくれば、体積の求め方は4年生の面積の勉強方法と同じです。
4年生のときと同じくややこしい形の立体が出てきます。解き方が分からなくなってきたら、4年生の問題集を使って練習すると分かりやすいです。
※関連記事：4年生の勉強内容：面積の求め方など単元別おすすめの勉強法を紹介！
この単元では、「ある数が2倍、3倍になればそれにともなって関連する数も2倍、3倍と変わっていくこと」を習います。
1個100円のリンゴが2個売れたら2倍の200円、3個売れたら3倍の300円になるという具合です。
上記のような「1個100円のリンゴが3個売れたら何円になるか」「1本80円のエンピツが2本売れたら何円になるか」といった基本レベルの問題を自分でつくってみましょう。比例のポイントを感覚的に理解しやすくなります。
この単元はいくらでも問題をむずかしくできるため、解き方を覚えようとするとレベルが上がってきたときに余計ややこしくなります。
2倍、3倍ではなく4倍、9倍になる場合もあります。
たとえば、1辺の長さが3cmの正方形があるとして、辺の長さが2倍、3倍となったら正方形の面積がどう変わるかを求める問題が出てきます。
3cm×3cmで面積は9cm2になります。1辺の長さが2倍になると、6cm×6cm=36cm2です。面積は4倍になっています。1辺の長さが3倍になれば、3倍×3倍で面積は9倍です。
言いかえると、2倍×2倍だから4倍になるのです。
問題そのものはそこまでむずかしくはなく、丁寧に問題量をこなせば大抵の子は解けるようになります。
ただし、2倍、3倍へと変化していく仕組みを感覚的に理解できないと、「とりあえず出てきた数字をかけ算する」という作業的な解き方になります。そうなると、上記のような面積や体積の問題でつまってしまいます。
2倍、3倍に変わる量がある場合と、そうでない場合の区別をできるようにしましょう。
【2倍、3倍に変わる例】
1個100円のリンゴを買ったときのリンゴの代金
【2倍、3倍に変わらない例】
気温15度で100個売れたアイスが、気温30度のときに売れる数。気温が2倍、3倍になったからといってアイスが2倍、3倍売れるわけではない。
【数字が変わらない例】
10歳の子どもと40歳の父親の年齢差。20年後も30歳差のまま変わらない。
自分でこういう例を考えて、2倍、3倍に変わる場合とそうでない場合を区別できるようにしておきましょう。
合同とは、形も大きさも同じという意味です。
2つの図形（三角形か四角形）を並べて、それらの図形が合同かどうか、合同なら対応する辺と角はどれかを判断する単元です。
この単元のおすすめの解き方は2種類あります。それぞれ説明します。
教科書や問題集に描かれている2つの図形をみてどちらも同じ向きをしていたら、合同かどうかを判断しやすいです。
ところが、2つの図形の向きがそれぞれ違っていると、急にわかりづらくなります。逆向きになったり、横を向いたりしていると同じ形をしているかどうか判断できません。
こういう場合、教科書や問題集ごと図形をゆっくりとクルクル回してみましょう。向きを変えてみると図形が見やすくなり、同じかどうか判断しやすくなります。
合同な図形は対応する辺の長さが同じで、対応する角の大きさが同じです。
「合同」という条件からわかることをすべて図形に書き込みましょう。
対応する辺の長さが何cmか、角度は何度なのか。
三角形や四角形の内角の和を使って計算すれば、角度が書かれていない角の大きさも求められます。
これら2つの解き方は中学受験でも高校受験（中学生の定期テスト）でも必須の方法です。
どちらもマスターしておきましょう。
※関連記事：平面図形・空間図形の解き方解説
4年生では分母が同じ分数のたし算・ひき算を習いました。5年生では分母の違う分数のたし算・ひき算と、分数のかけ算・割り算を習います。
分数の計算を得意にするコツは「約数・倍数」です。完璧にマスターしましょう。
2つ3つの数字を見たら3秒以内にそれらの最小公倍数と最大公約数が思い浮かぶようになるまで繰り返し練習しましょう。
8と12をみたら、最小公倍数は24で、最大公約数は4です。
20と30なら、最小公倍数は60で、最大公約数は10です。
たくさん問題を解いていると、この計算力（というか暗記に近いですが）はすぐに身に付きます。
「たし算・ひき算よりもかけ算・割り算のほうが楽だな～」という印象になれば、最小公倍数と最大公約数はマスターしたと言えるでしょう。
通分・約分はほぼできたようなものです。
分数のたし算・引き算で通分を使います。通分とは「分数の分母を同じ数字すること」です。1/3+2/3など、分母が同じなら計算できるからです。
1/2+2/5の計算を例にして、通分の仕方を説明します。
【計算例】
1/2+2/5
=5/10+4/10
=9/10
【計算の仕方】
分母を2と5の公倍数である10にします。
②1/2の2を5倍する。分子の1も5倍する。→5/10
③2/5の5を2倍する。分子の2も2倍する。→4/10
③5/10+4/10となり、分子どおしを足し算する。→9/10
分数のかけ算・わり算で約分を使います。約分とは「分母と分子を同じ数字で割り算して、できるだけ小さい数字にすること」です。
約分の仕方を計算例を使って説明します。
【計算例】
2/5×15/4
=1/5×15/2
=1/1×3/2
=3/2
【計算の仕方】
分母と分子をそれぞれの公約数で割ります。
①分母…5と4、分子…2と15→（分母の5と分子の15）（分母の4と分子の2）をそれぞれ割り算できる
②分母の5と分子の15をそれぞれ3で割る→分母は1に、分子は3になる
③分母の4と分子の2をそれぞれ2で割る→分母は2に、分子は1になる
④残った数字を分母どうし、分子どうしかけ算する→分母は1×2、分子は1×3
この単元では、ひし形や台形の面積を求めたり、底辺と高さが同じで形のちがう三角形の面積を求めたりする問題が出てきます。
ほとんど同じ問題が中学受験や中学校の定期テストにも出てくるほど難易度の高い単元です。
この単元のポイントは、感覚ではなく理屈で解くことです。図形ごとの性質を「パッと思いだせる」くらいまで覚えておきましょう。
下記の図をご覧ください。底辺と高さが同じで形のちがう2つの三角形です。
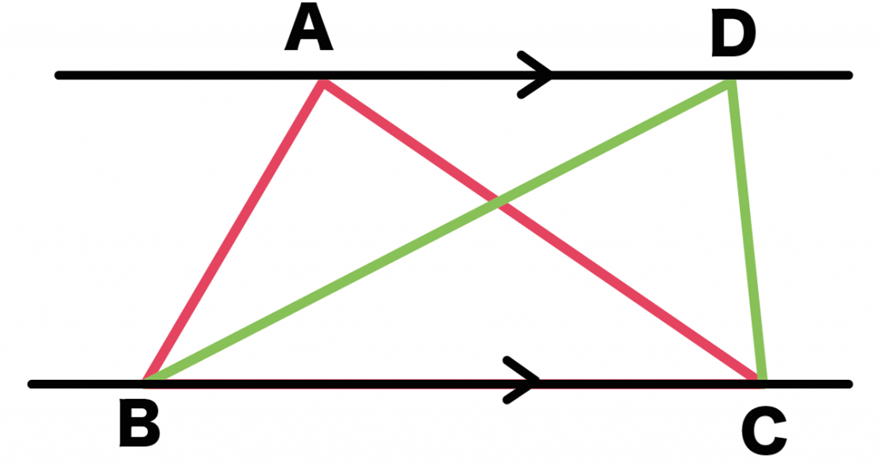
三角形ABCと三角形DBCは同じ面積です。底辺と高さが同じだからです。でも2つの三角形の形は違います。
小学生のころの私はこうした図を見せられて「ホントに同じ体積なの？？」と違和感ありありでした。
合同な三角形なら、形や大きさが同じなので面積も同じになると感覚的に理解できます。ところが、形が違うと面積が同じになのかどうか感覚的にわかりづらくなります。
三角形の面積は下記の公式で求めます。
「底辺×高さ÷2」
この公式にのっとって考えれば、上記の2つの三角形は底辺と高さが同じですから、確かに面積も同じになるはずだというのは理屈で理解できます。
図形が苦手になる子は、理屈ではなく感覚的に解こうとしています。
小学生のころの私もそうでしたが、「形が違うのになぜ面積が同じなの？」と疑問に感じるのです。
前述の「合同」で「辺の長さや角の大きななど、わかるところを図形に書き込みましょう」とお伝えしましたが、これも感覚ではなく理屈で解けるようにするためです。
わかっている条件を整理して、「～ということは、この辺の長さは何cmになるはず」「～ということは面積が同じになるはず」と、理詰めで答えを出していきます。
この方法に慣れていきましょう。
こうした考え方は算数や数学だけでなく、中学受験の理科や中学校の理科でも使います。慣れておくととても大きな武器になります。
6年生や中学校の数学に直結し、中学受験で合否の分かれ目の1つにもなる単元です。
問題を解きはじめる前に、「答えはいくらくらいになりそうか？」を考えてみましょう。
例えば「5年生の平均身長」を求める問題が出てきたら、まず答えを予想します。「5年生の身長」ですから130-140cmくらいですよね。
答えを予想してから問題を解いてみて、自分の出した解答が「250cm」となっていたら「多分間違ってるよね」と気づきます。数字の足し忘れがある、割り算にしないといけないのにかけ算にしていたなど、間違えてしまっているポイントに自分で気づきやすくなります。
平均や割合は感覚的に数字を扱えるようになれるかどうかがポイントですから、苦手にしている子にいくら理屈で説明してもピンときません。出てきた数字をとりあえずかけ算するといった「作業」で終わりがちです。
「もとにする量」と「くらべる量」で計算する方法を習います。この方法を使えばいったん解きやすくなりますが・・・、
まっったく問題を解けないとき以外は絶対に使わないほうがいいです。
なぜなら5年生の基本問題以外では、むしろ間違いを誘発するからです。そもそもどれが「もとにする量」「くらべる量」なのかが分からない子も少なくありません。そういう子にとっては「考えないといけないこと」が増えるだけで、苦手をさらに苦手にする一因になります。
応用問題でも、6年生に習う割合でも、中学受験の算数でも、さらに中学校に入ってからも、割合を解けるようにならない原因になってしまいます。
※関連記事：割合の問題の解き方
条件が1つだけ、たとえば下記のような問題の場合、とりかえずかけ算をしましょう。
「クラスに男子が20人います。この人数は女子の0.8倍です。クラスの人数は何人でしょうか。」
20×0.8=16（人）
これで女子は16人いるとわかります。男子と女子合わせて何人いるか聞かれているので、
20+16=36（人）
が答えです。簡単に答えが出ます。
条件が2つ以上というのは、たとえば下記のような問題です。
「近所のスーパーでは、1個1000円のお弁当が2割引きで売られている。このお弁当は5時を過ぎるとさらに3割引きになる。5時以降に買うと1ついくらか。」
1つ目の条件は、「1個1000円のお弁当が2割引きされるといくらになるか」です。
2つ目の条件は「2割引き後のお弁当が3割引きされるといくらになるか」です。
条件ごとに分けて解くのですが、1つずつに分けてしまえば、先述の「とりかえずかけ算をする」という方法で解けます。
1000×0.8=800（円）
800×0.7=560（円）
と別々に計算します。もし間違って、
「1000×0.2=200（円）」としてしまっても事前に答えを予想してから解いていれば、こんなに安くなるはずがないと気づけます。
この、条件を整理する（条件ごとに計算する）という方法は算数だけでなく、理科の実験・観察問題もそのまま使えます。
よく、国語の長文読解は得意なのに算数の文章問題や理科の実験・観察問題は苦手という子がいます。国語の長文読解と算数・理科の文章問題では読み方が違うからです。
この方法をマスターしておけば、理系教科はとても解きやすくなります。
「分速200mで10分だと何m走れるか（2000m）」といった内容を習う単元です。
「速さ」も、先ほどの「割合」とまったく同じ考え方・解き方をします。
最初は「はじき」（「きはじ」）を使うとで解きやすくなりますが、慣れたら「はじき」を使わずに解くようにしてみましょう。
習いたてのときは便利な解き方なのですが、応用問題になるとやはり間違いの元になってしまい、伸び悩みになりがちです。
※関連記事：速さの解き方のコツ
この単元も苦手にしている子が多いですが、問題の種類別に解き方が決まっています。
この単元のコツは「図形の区別」です。名称・性質をセットで覚えておきましょう。
| 円 | 端から端までの距離がどこも同じ。 「端から端：直径」 「直径の半分：半径」 「円の真ん中：中心点」 |
| 正多角形 | 辺の長さ・角の大きさがすべて同じ。 形が決まっている。 |
| 角柱 | 上の面と下の面（＝底面）が同じ形で、横の面（側面）は四角形 |
| 円柱 | 上の面と下の面（＝底面）が円で、横の面が1枚の長方形をクルっと回したような形。 筒状。 |
図形を苦手にしている子は、これらの性質をよく分かっていないまま問題を解いていることがよくあります。解説を読んでも「なぜ答えがそうなるのか」が分からないままです。
知っておくだけで問題の何割かに正解できますし、解けば解くほど性質が頭に入ってくるのでさらに問題を解きやすくなります。
※関連記事：平面図形・空間図形の解き方
図形が得意な子は図形の性質を手と目で把握しています。5年生の図形のなかでも、正多角形はフリーハンド（定規やコンパスを使わない）で描いてみましょう。
慣れないうちは辺の長さがバラバラになったり、角度がつじつま合わせのように変な大きさになったりします。
慣れてくると、「それぞれの正多角形がどのような形をしているのか」を感覚的に把握できるようになります。
家庭での学習ツールは大きく2つあります。
です。それぞれの選び方を説明します。
市販教材はネットや本屋さんで子どもと一緒に選ぶのがおすすめです。
親が気に入ったものを買って子どもにさせるのも良いですが、子どもがする気になってくれなかったら意味がありません。
「主婦と生活社」の『すみっコぐらしシリーズ』や学研の『ドラゴンドリルシリーズ』など、子どもの興味を引きながら楽しく勉強できるドリル・問題集がたくさんあります。
子どもが気に入ったものを使うと、楽しく勉強に取り組んでくれるようになります。
毎朝5分の学習習慣をつけるためのドリル（『早ね早おき 朝5分ドリルシリーズ』）もあれば、中学受験に向けて思考力や応用力を養う問題集（『トップクラス問題集』）もあります。
学習目的に合わせて選ぶようにしましょう。
※関連記事：5年生向けの市販教材をこちらの記事で学習目的別に紹介しています。
5年生算数のおすすめドリル・問題集
5年生国語のおすすめドリル・問題集
昔から国語辞典を使う子は賢くなると言われています。
何かを考えるとき、人間は言葉を使います。語彙が豊富なほうが思考力や表現力が豊かになります。
それだけでなく、国語辞典を自分で使う習慣をつくると、
「自分で学ぶ習慣をつくること」
もできるようになります（コクリコ「辞書引き学習で国語の成績が向上」より）。
受験する・しないに関わらず、国語辞典をリビングに常備し、自分で調べる習慣をつくっておきたいですね。
※関連記事：国語辞典を使う習慣をつくって語彙力・読解力を伸ばす方法
※関連記事：おすすめの国語辞典：子どもに合う辞書の選び方や辞書の引き方も解説
学習の質を高めるために多くのご家庭では通信教育が利用されています。
カリキュラムが明確にありますし、タブレット学習なら「復習したほうがいい問題」をAIが自動表示してくれるので「何を勉強すればいいか」を悩むことがなくなります。
しかも、ウェブ授業や個別対応も標準プランの範囲内にあります。
難関中学、最難関中学（首都圏御三家、灘中学、ラサール中学など）を目指しているならZ会がおすすめです。1年生から思考力アップ講座を受けられている方が多いです。
下記のような特長があります。
※関連記事：Z会中学受験コースだけで難関中学に合格する方法
Ｚ会の通信教育 中学受験コース中学受験対策の通信教育として進研ゼミも多くの受験生に選ばれています。楽しく、自信をつけながら学べるという特徴があります。
※関連記事：進研ゼミ小学講座の特徴と効果的な利用
算数に苦手意識のある子を「算数好き」にする通信教育としてRISUが注目を集めています。
ゲームのようにステージをクリアすればするほど算数の問題を解けるようにしていくシステムです。
小学校の勉強先取りはもちろん中学受験の問題もたくさんあり、RISUの会員で四谷大塚の全国小学生学力テストやSAPIXの模試で全国1位を取っている子も出ています。
費用のシステムが分かりにくいので、その解説も含めて下記の記事で紹介しています。
中学受験をするご家庭では、5年生は本格的な受験対策真っ只中です。
算数が伸び悩んだり、国語の記述問題に苦労する子が続出する時期でもあります。
※関連記事：【中学受験】算数が苦手な子必見！家庭でできる「算数の伸ばし方」をお伝えします！
※関連記事：【中学受験】国語のおすすめ問題集：学年別に漢字・読解・作文・入試対策問題集を紹介
※関連記事：おすすめの記述・作文問題集
最近の中学入試の問題は下記のような特徴があります。
ひと昔前なら、大量の知識をインプットして正確にアウトプットする能力の高い子が志望校に合格しやすかったです。
最近では、そうした「処理能力の高い子」よりも「思考力・表現力の高い子」や「明確な学習方針で勉強してきた子」のほうが合格しやすくなっています。
その1つが英語教育です。5年生では英語が必修化されていますが、小学校の進度を先取りして中学英語の学習に入っているご家庭も数多くみられます。
英検を取得しておくと英語利用できる私立中学がたくさんあります。
特に、英検®3級以上あればかなり優遇され、慶應湘南藤沢小などの難関校の英語も解けるようになってきます。
※関連記事：入試で英検®が使える東京の私立中学一覧
※関連記事：入試で英検®が使える神奈川、埼玉、千葉の私立中学一覧
※関連記事：入試で英検®が使える関西の私立中学一覧
入試問題のタイプの変化だけでなく、難易度も上がっています。
例えば、東京都の御三家の1つである開成中学で30年前に出題された算数の問題が、今では偏差値40〜50くらいの学校で出題されています。
30年前の超難問は、今の標準問題なのです。
子どもの勉強状況をみて、復習の機会を作ってあげたり模試の分析を一緒にしたりと、保護者の方のサポートがとても重要になってきます。
※関連記事：【中学受験】勉強スケジュールの作成・管理方法を解説：親はどこまでサポートすればいい？
受験対策をされる場合、約8割の方は塾で対策をされています。
ただ、その8割の方のなかでも利用する塾の種類や方法はさまざまです。
集団指導塾のみだった方が途中から個別指導塾や家庭教師を併用される場合もあります。
6年生の冬（入試直前）に算数や理科でプロ家庭教師を活用して10-20点アップをする場合や、難関中学入試に向けて低学年から家庭教師を利用する場合など、学習手段も多様化しています。
※関連記事：【中学受験】個別指導塾だけで大丈夫！？
※関連記事：【中学受験】個別指導塾併用のメリット
※関連記事：【中学受験】小学生の家庭教師はいつからがいい？
※関連記事：中学受験・高校受験・大学受験でプロの家庭教師の選び方
状況や時期に応じて上手に活用したいですね。
さらに、家庭学習のみで受験対策をされているご家庭もあります。
首都圏で偏差値60以上の中学校に合格されているご家庭でもそうした方が2割ほどいらっしゃいます（ひまわり教育センターより）。
ご家庭の学習方針次第では、「塾なし」でも受験対策ができるような環境ができています。
※関連記事：【中学受験】塾なしは無理？家庭学習のみで志望校に合格できるおすすめの学習方法を紹介します
第一志望校は4-5年生で決定するご家庭が多いです。
同時に、第二志望校や「安全校」の候補を探しておくと良いですね。
※関連記事：【中学受験】志望校はいつまでに・どうやって選ぶ？おすすめの決め方を紹介します！
かつては「大学進学実績」がほぼ唯一の判断基準でしたが、今は大きく状況が変わっています。
少子化が進むにつれて私立中学では学びの多様化が進んできているからです。
など様々です。
前述のように、英語入試を導入する私立中学も非常に多くなっており、英語教育に力を入れているご家庭は将来の選択肢がとても多くなっています。
※関連記事：入試で英検®が使える東京の私立中学一覧
※関連記事：入試で英検®が使える神奈川、埼玉、千葉の私立中学一覧
※関連記事：入試で英検®が使える関西の私立中学一覧
しかも最近では公立中高一貫校が人気です。公立の費用で私立のような6年一貫の教育環境を手に入れられます。
あまりの人気で、開設時には偏差値50弱だった公立中高一貫校が数年後には偏差値60近くまで上昇しているケースもあります。
作文が必須だったり、複数の教科をまたいだ試験になっていたりと、私立中入試とは全く対策方法が違っています。
※関連記事：人気急上昇中の公立中高一貫校の魅力とは？私立中との入試制度の違いや対策方法を解説します！
※関連記事：【中学受験国語】おすすめの記述・作文問題集：書き方の基本から難関レベル対策まで
5年生は、「受験を新たにはじめるご家庭」と「中学受験をやめて高校受験に切り替えるご家庭」が多くなる時期でもあります。
それまで受験を考えていなかったのに、子どもが急に
「受験したい！」
と言ってきたり、家の近くの公立中学が中高一貫校になると決まった。
といったことがよくあります。
5年生からでも受験対策は十分間に合います。
ただし、子どもの受験勉強への持っていきかたに悩んだり、
大手の塾に入れる場合にはカリキュラムが合わなかったりと、
対策の仕方に工夫が必要です。
※関連記事：【中学受験】5年生からでも塾で間に合う？巻き返すための勉強方法と親のサポート方法
逆に、中学受験の勉強を数年続けたものの、
「本当に子どもにとってプラスになっているだろうか」
と悩むご家庭も出てきます。
成績があがらず親子ともにストレスが大きかったり、子どもが友だちと遊ぶ時間が減ってさびしそうにしていたりと、
当初思い描いてたイメージを違う状況になることもよくあります。
その場合は、本当にこのまま受験勉強をつづけるかを子どもと何度も相談しましょう。
子ども自身のやる気が1番大切ですが、惰性で続けられるものでもありません。
※関連記事：中学受験やめようかなと思ったら：やめどき、判断基準を3つ紹介します！
ただ、もし「成績が原因」なのであれば、転塾して状況を好転させているご家庭が8割もいらっしゃるというアンケート結果もあります（かしこい塾の使い方より）。
転塾して状況を変えてみるなら、5年生夏までがおすすめです。
※関連記事：【中学受験】転塾はいつまで？成績があがる塾を選ぶおすすめのポイントを3つ紹介！
5年生の算数は6年生や中学受験、中学の定期テストにもそのままつながっていくほど、難易度の高い単元がたくさん出てきます。
つまずきやすい単元が連続して出てくるため、復習が間に合わずなかなか解けるようになりません。
解けないとやはりイヤになります。算数嫌いになります。
条件を整理して理詰めで解く方法を身につけておけば、いくつかの単元はかなり解きやすくなります。
得意な単元をいくつかつくっておけば自信になります。苦手な単元にも「できるようになるはず！」と取り組みやすくなります。
Z会 小学生コースの案内
※関連記事：Z会小学生コースの進め方：自主性や考える力を伸ばせる問題の特徴を紹介
This website uses cookies.