【中学受験】割合を解くコツ：損益算や濃度算などの割合の文章問題の解き方や勉強法を紹介します

Pocket

中学受験の算数は小学校で習わない単元や、小学校で習った単元をさらに応用させている単元がたくさんあります。

なかでも「割合」は入試の中心であり、得意な子はかなり合格に近づけます。

割合を苦手にしている子も多いですが、コツを身につけてしまえば得意になります。

そこで、今回の記事では

なぜ割合がむずかしいのか
どうすれば割合を解けるようになるか
割合対策のおすすめの問題集

をお伝えます。

特に、割合の基本から応用に入るあたりでつまずいてしまっている人は参考にしてください。

Ｚ会の通信教育　中学受験コース

※Z会の中学受験コースのメリットや活用法を下記の記事で紹介しています。
Z会中学受験コースだけで難関中学に合格する方法

参考：Z会

中学受験算数：割合の基本
百分率とは何か？
1. 百分率の使い方
2. 百分率の計算方法
百分率を求める練習問題
割合の求め方（練習問題付き）
中学受験の割合を得意にするコツ
中学受験算数で割合が重要な理由
割合が苦手になる子の特徴
割合の演習におすすめの問題集
ほかの科目の問題や解き方のコツ
まとめ

中学受験算数：割合の基本

中学受験をする小学生向けに、「割合」の基本を簡単に解説します。

割合とは？

割合とは、2つの数量の関係を表す方法です。たとえば「全体の何分のいくつ」や「全体の何%」などのように表します。割合は、比や百分率（%）で示されます。

割合の求め方

ある数量が全体のどのくらいかを求めるには、「割合 = くわべる量 ÷ もとにする量」 で計算します。たとえば、30個中6個が赤なら、6 ÷ 30 = 0.2、つまり20%です。

以下の図をご覧ください。割合を求める公式を図にしたものです。

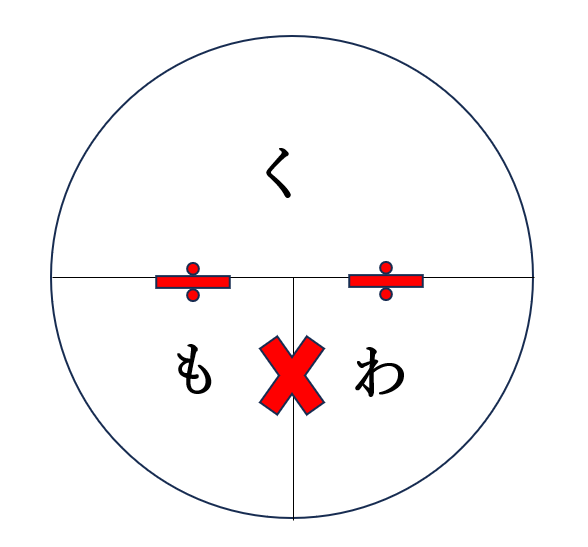
速さの公式である「は・じ・き」と同じように覚えると使いやすいです。

割合＝比べる量÷もとにする量
もとにする量＝比べる量×割合
比べる量＝もとにする量×割合

割合の使い方

割合は、比べたい物の大小を比率で見るときに便利です。買い物での割引、得点率、速さの比較など、日常の様々な場面で役立ちます。

百分率とは何か？

割合の単元では、「百分率」という言葉が出てきます。百分率とは、「全体を100としたときにその一部がどれくらいを占めているか」を示す表現方法です。「%」という記号を使います。

例えば、「全体で100個あるうちの20%は何個？」と聞かれたら、「20個」が答えになります。

また、クラスの40人中8人が図書委員だとします。このとき、図書委員の割合を百分率で表すと、8 ÷ 40 × 100 = 20%となります。

このように、全体の中でどのくらいの割合かをひと目でわかりやすく示すことができます。

百分率の使い方

百分率は、身の回りでよく使われています。たとえば、テストで「80%の正解率」と聞けば、100問中80問が正解だったことがわかります。

また、スーパーなどの割引でもよく見かけます。たとえば、「商品が20%割引」とあれば、もともとの値段から20%分の割引がされていることがわかります。

このように、百分率は私たちが日常で簡単に割合を理解できるようにするための便利な方法です。算数でもこうした「〇%割引」の問題はよく出てきます。

百分率の計算方法

百分率を求めるには、まず対象の数を全体の数で割り、その結果に100をかけます。

「割合 = （部分 ÷ 全体）× 100」

前述の「割合を求める公式」で出した答えに100をかければ百分率になります。

たとえば、学校で40人中10人が図書委員だとすると、割合は10 ÷ 40 × 100 = 25%です。こうすることで、割合を百分率で表すことができ、全体に対してどのくらいの割合かが明確になります。

百分率を求める練習問題

それでは、百分率の問題を解いて練習してみましょう。

クラスの30人中12人が運動部に所属しています。運動部に所属している生徒の割合を百分率で求めなさい。

解答・解説：12 ÷ 30 × 100 = 40%
運動部に所属している生徒は全体の40%です。

80個のリンゴのうち、20個が青リンゴです。青リンゴの割合を百分率で求めなさい。

解答・解説：20 ÷ 80 × 100 = 25%
青リンゴは全体の25%です。

50問のテストで40問正解しました。正解率を百分率で求めなさい。

解答・解説：40 ÷ 50 × 100 = 80%
正解率は80%です。

100円の商品の30円が割引されています。割引率を百分率で求めなさい。

解答・解説：30 ÷ 100 × 100 = 30%
割引率は30%です。

60人の児童のうち45人が算数が得意と答えました。算数が得意な児童の割合を百分率で求めなさい。

解答・解説：45 ÷ 60 × 100 = 75%
得意な児童は全体の75%です。

おこづかい500円のうち100円を貯金しました。貯金の割合を百分率で求めなさい。

解答・解説：100 ÷ 500 × 100 = 20%
貯金の割合は20%です。

200本のエンピツのうち、30本が赤色でした。赤色のエンピツの割合を百分率で求めなさい。

解答・解説：30 ÷ 200 × 100 = 15%
赤色のエンピツは全体の15%です。

クラスで読書が好きな児童が30人中12人でした。読書が好きな児童の割合を百分率で求めなさい。

解答・解説：12 ÷ 30 × 100 = 40%
読書が好きな児童は40%です。

10枚のカードのうち、2枚がスペシャルカードでした。スペシャルカードの割合を百分率で求めなさい。

解答・解説：2 ÷ 10 × 100 = 20%
スペシャルカードは全体の20%です。

75本のチョコレートのうち、15本がミント味です。ミント味の割合を百分率で求めなさい。

解答・解説：15 ÷ 75 × 100 = 20%
ミント味は全体の20%です。

割合の求め方（練習問題付き）

どうすれば割合を得意にできるか。いくつかやり方がありますが、厳選して3つお伝えします。

※関連記事：中学入試によく出る割合の問題

かけ算からはじめる

割合の問題が出てきたら、とりあえず「全部かけ算からはじめましょう」。

割合の問題で、「割合を求めなさい」という問題はほぼ出ません。

「何人ですか？」「何kgですか？」など、具体的な数字を求めるか、
それをもとにして、「どちらがどれだけ多いか/重いか/安いか」などを求める問題が大半です。

ここで、最初の公式を活用します。割合を求めないのなら、使う公式は下記のどちらかです。

くらべる量＝もとにする量×割合
もとにする量＝くらべる量÷割合

「かけ算」か「わり算」です。割合の問題は、答えを出すまでに何度か計算をしますが、途中式は「くらべる量」を求める計算のほうが多いです。

とりあえずかけ算して答えを求めるようにしましょう。

練習問題

下記の問題を解いてみましょう。

【問題(1)】

A. 120人の3割は何人？

B. 50kgの40%は何kg？

C. 1クラス40人のうちが男子で、今日は女子が3人欠席した。今日の出席者で、男子と女子はどちらがどれだけ多い？

【問題(1)】の解答

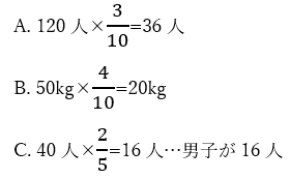
ご覧のように、かけ算で求められます。

わり算を使う問題で間違ってかけ算を使うと、異様に数字が大きくなります。数字が大きくなると、間違いに気づきやすくなります。

【問題(2)】

A. 120人のうち36人は何割？

B. 20kgは50kgの何%？

C. 1クラス40人のうち、15人が男子。男子は女子の何%いる？

問題(2)の解答

【もしかけ算するとどうなるか】

A. 120人×36人＝4320割？

B. 20kg×50kg=1000%?

C. 40人-15人＝25人…女子は25人
15人×25人=375=37500%？

「4320割」「1000%」なんて聞いたことないですね。

Cの問題でも、男子より女子が多いのが問題をみれば感覚的にわかりますが、かけ算をすると男子は女子の37500%もいることになってしまいます。

とりあえずかけ算にしてみれば、こうした「明らかに違和感のある大きな数字」になります。この時点で、「あ、違う！」と気づけます。

どうしてもわからないときはかけ算をしてみてください。

比例式を得意にする

比例式を得意にすると、割合を解きやすくなります。

比例式は割合の問題を解くときによく使います。比例式という名前が小難しそうですが、仕組みは単純です。

「＝」（イコール）をはさんで、外にある数字どうし、内にある数字どうしをかけます。

※比が苦手な人向けに以下の記事でくわしく解説しています。
逆比とは：中学受験の比の応用問題でよく使う逆比の使い方と練習問題

比例式の練習問題

たとえば、下記のような問題でつかえます。

【問題】

ホットケーキをつくるために、薄力粉と砂糖が必要です。ホットケーキ1枚で薄力粉80g、砂糖を20g使います。自宅にある薄力粉300gをすべて使うとすると、砂糖は何g使えばいいでしょうか。

【解答】

薄力粉と砂糖の分量を比で表します。

薄力粉 : 砂糖 = 80 : 20
薄力粉 : 砂糖 = 4 : 1

薄力粉を300g使うという条件を使って比例式で表します。

薄力粉300g : 砂糖□g = 4 : 1
□ × 4 = 300 × 1
□ = 300 ÷ 4
□ = 75g

比例式を使うと、「くらべる量」「もとにする量」といった概念を使いません。

すると、「かけ算かな？」「わり算かな？」と悩む必要がなくなります。

比例式を覚えておけば、とても強い味方になってくれます。

そのためには比の勉強が欠かせません。

問題文に数字を書き込む

割合の問題は何%、何割という抽象的な数字が並んでおり、イメージしづらいです。

問題文に具体的な数字を書き込みながら解きましょう。

これは平面図形・空間図形の解き方と同じですが、数字を書き込むだけでかなり解きやすくなります。

※関連記事：平面図形・空間図形の解き方

例題で解説

先ほどの例題を使って説明します。

問題

前述のように、薄力粉と砂糖の分量は4:1だとわかりました。わかった時点で問題文にそれを書き入れます。

ホットケーキ1枚で薄力粉80g（④）、砂糖を20g（①）使います。自宅にある薄力粉300g（④）をすべて使うとすると、砂糖（①）は何g使えばいいでしょうか。

のような具合です。

解説文をいくら読んでもピンとこないことってありますよね。算数の解説文が苦手な子は「4:1」といった抽象的な式と「薄力粉300g」といった具体的な数字をつなげて考えるのが苦手です。

式は抽象的でも問題文は「薄力粉300g」のように具体的に書いてくれていますから、新たに把握できた数字を問題文に書き込むと、設定された状況を具体的に把握しやすくなります。

中学受験の割合を得意にするコツ

中学受験算数の割合を解くにはいくつかのコツを使います。問題の種類別にお伝えします。

オーガニックの出産祝い【Haruulala】

計算のコツ

割合はどのように計算すれば良いかがややこしくなりがちです。

割合の問題全般で使える計算のコツを紹介します。

割合を小数になおす

割合はいったん小数になおしてから計算しましょう。

割合には～%、〇割といった表し方があります。それぞれ小数になおすといくらで表すのか確認します。

200%→2
100%→1
50%→0.5

5割→0.5
3割→0.3

損益算（原価・定価・利益・割引）のコツ

損益算の解き方のコツを紹介します。

損益算とは、原価1000円の商品に1割の利益を見込んで定価をつけて10個売ったらいくらの売上になったか。などの問題を解く方法です。

原価・定価・利益・割引の意味を覚える

まず、原価・定価・利益・割引の言葉の意味を覚えて区別できるようにしましょう。

下記の図をご覧ください。

商品がスーパーなどの店頭に並ぶまえに、お店は別のお店（卸売業者）からその商品を仕入れています。これを原価、または仕入れ値（①）と呼びます。お店は原価（①）に利益（②）をつけて定価（③）にして売ります。中学受験の問題では、定価からさらに割引して売る設定がほとんどです。

原価：仕入れるときに買った値段（①）
利益：原価につけた利益（②）
定価：原価＋利益の値段（③）
割引：定価から値段を安くする

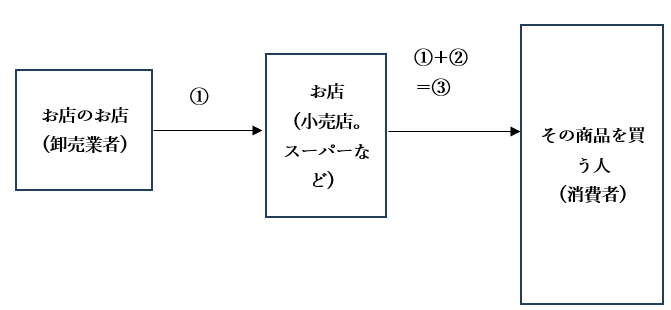
例えば、1個100円で仕入れて（①＝100円）、20円の利益（②）を見込んで定価120円（③）で売ったところ、売れなかったので1割引きして108円（120×0.9）にして売る。というように問題がつくられています。

消費者が商品を購入するまでの大まかな流れと上記4つの用語の意味を覚えておくと、問題文を理解しやすくなります。

〇割引は1から引いて小数にする

「割引」と出てきたらまずその割引の数字を小数にし、1からその小数を引いて定価にかけ算しましょう。

例えば「120円の商品を1割引きにする」とあれば、「1割引→0.1」にします。さらに、「1-0.1=0.9」にします。

この「0.9」という数字を定価にかければ「割引後の値段」を求められます。

〇%増は1をつけて小数にする

「〇%増」と出てきたらその%の数字を小数にし、1にその小数を足して計算しましょう。

例えば「原価100円の商品を20%増で売る」とあれば、「20%→0.2」にします。さらに、「1+0.2=1.2」にします。

この「1.2」という数字を原価にかければ「〇%増にした値段（定価など）」を求められます。

濃度算のコツ

割合では「濃度算」もよく出てきます。「10%の食塩水100gをほかの食塩水と混ぜる…」といった問題です。

濃度算を苦手にしている小学生は多いですが、コツをつかめばそれほどむずかしくありません。

水・食塩・食塩水の量を求める

まず、食塩水の問題が出てきたら「水」「食塩」「食塩水」の3種類の量を求めましょう。

問題文で何を聞かれていても、とりあえずこの3種類を求めます。なぜなら、どの問題でもほぼ必ずこの3種類の数字をすべて使うからです。

例えば、10%の食塩水200gを別の濃度の食塩水300gと混ぜて7%にしたとします。300gの食塩水の濃度は何%だったのかを求めます。

「10%の食塩水」の量は分かりますが、「食塩」と「水」の量が書かれていません。以下のように求めます。

【10%の食塩水200g】
食塩：200g×0.1（10%）＝20g
水：200g-20g＝180g

【混ぜたあとの食塩水7%】
食塩水：200g+300g=500g
食塩：500g×0.07（7%）＝35g
水：500g-35g＝465g

上記のように計算して、とりあえず3種類とも求めておきましょう。

すると、7%の食塩水のなかに35gの食塩が入っていると分かります。10%の食塩水200gには20gの食塩が入っていたので、混ぜたほうの食塩水（濃度が分からない300gの食塩水）には35g-20g=15gの食塩が入っていたことが分かります。

300gの食塩水に15gの食塩が入っているので、
15g÷300g=0.05=5%と分かります。

上記の例では、「水の量」を求めなくても答えは出てきます。ですが、水の量を求めないと解けない問題もあります。

仮に要らない計算だったとしても引き算1つで済む程度です。5秒くらいで終わる計算です。多少の回り道になったとしても「とりあえず」求めておけば、自力で正解にたどりつくことができます。

中学受験算数で割合が重要な理由

算数は中学入試で合否を決める重要な科目といわれます。そのなかでも割合は特に重要な単元です。

その理由をお伝えします。

割合の問題が入試頻出だから

まず、割合の問題自体が入試ではよく出てきます。

基本的な問題は出てきませんから、一定以上の解く力がないと割合の問題は全滅してしまいます。

割合をつかって解く問題が多いから

次に、割合はほかの単元でもよく使います。

比、速さ、図形などでは、応用レベルになると割合をつかう問題が非常に多くなります。

中学入試に頻出で、さまざまな単元の応用問題で活用されるため、割合を得意にしているかどうかが入試の合否に大きな影響を与えます。

入試まで苦手克服しづらいから

割合を1度苦手にすると、入試までずっと苦手なままになりやすいです。

算数の苦手単元を学年別に調査した結果をみると、下記の表のようになったそうです。

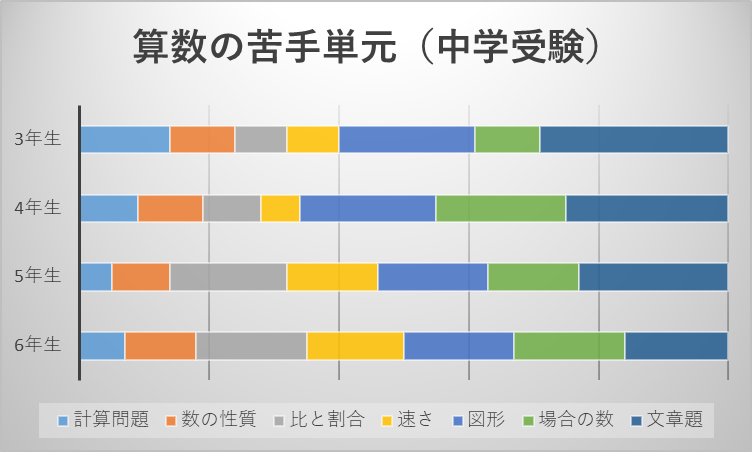
学年があがるにつれて比や割合は苦手な子が増えていきます。

比と割合以外の単元をみると、5-6年生で苦手にしている人の割合は小さくなっています。ところが、比と割合だけは苦手な人が2倍に増えています。

苦手を克服できないまま、あるいは新たに苦手になってしまったまま入試に突入してしまっているものと思われます。

※比については下記の記事で解説しています
【中学受験】「比」の勉強方法

割合が苦手になる子の特徴

割合が苦手になる子は、なぜ苦手になったのでしょうか。

割合には「抽象的な数字を扱う」という特徴があります。この特徴がスムーズな理解をはばんでいるケースが大半です。

割合が苦手になる理由のなかで特に多いものは下記の3つです。

割合の表し方を統一していない
いつまでも公式に当てはめている
比が苦手

それぞれ説明します。

割合の表し方を統一していない

1つ目は、「割合の表し方の統一」です。

割合の表し方は下記の4種類あります。

分数
小数
百分率
歩合

1つの状況を説明するのに4種類の数字を使うと、大人でもこんがらがってしまいます。

たとえば、「Aさんの家の近所にあるスーパーに売っている商品はどの種類が多いのかを比較する」とします。

4種類の数字で表すと以下のとおりになります。

このスーパーにはどの商品が多いのか、パッと見て把握できません。
表し方がバラバラなので、感覚的にわかりづらいのです。

分数に統一する

割合はすべて分数で表すようにすると理解しやすくなります。

分数にすると、下記のようになります。

こちらのほうがかなりわかりやすいですよね。冷凍食品が多いスーパーだなとわかります。

分数への変換方法は単純です。下記の3パターンを覚えておきましょう。

いつまでも公式に当てはめている

苦手になる2つ目の理由は、「いつまでも公式に当てはめて解こうとしていること」です。

割合の公式といえば、

割合＝くらべる量÷もとにする量
くらべる量＝もとにする量×割合
もとにする量＝くらべる量÷割合

です。

この公式自体は便利で、割合を習いはじめた頃はこの公式に当てはめれば正解が出ました。下記のような方法で解きます。

【問題】

A. 200円の20%はいくらか。
※200円はもとにする量で、20%は割合

B. クラスの10%にあたる3人が受験する。クラス全員で何人か。
※10%が割合で、3人がくらべる量

【答え】

A. 200円×20%=40円
B. 3人÷10%=30人

割合、くらべる量、もとにする量が1つずつなら上記のように公式に当てはめるだけでスパっと答えが出ました。

このやり方だと問題が複雑になってくると対応しきれなくなります。

例えば、下記のような問題です。

「Aくんは2500円持ってスーパーに行きました。持っているお金のうち、2割で野菜を買い、残ったお金の3割で魚を買い、さらに残りの15%で飲み物を買いました。
Bさんは3000円持って17時に同じスーパーに行って買い物をしました。3割で野菜を買い、残ったお金の2割で魚を買おうとしたところ25%割引をしていました。さらに残ったお金の4割で飲み物を買って、98円の菓子パンを3つ買いました。
残ったお金は、AくんとBさんのどちらのほうが多いでしょうか。」

どれが「くらべる量」で、どれが「もとにする量」かわかりづらいです。条件がたくさんあって、公式に当てはめようとするとミスをしてしまいます。

比が苦手

苦手になる3つ目の理由は、「比が苦手」です。

割合の応用問題は比をつかいます。特に比例式（「5:〇=4:7」のような式）をつかって解く問題がよく出てきます。

連比のような割合と比を組み合わせた問題は、比を理解していないとそもそも解けません。

※比が苦手な人向けに以下の記事でくわしく解説しています。
逆比とは：中学受験の比の応用問題でよく使う逆比の使い方と練習問題

割合の演習におすすめの問題集

ポイントがわかったところで、実際に中学受験の「割合」の演習をして早く解きなれましょう。

おすすめの問題集を4冊紹介します。

『単元別基本問題集基本の制覇割合―中学入試算数』

単元別基本問題集基本の制覇割合―中学入試算数

出版社：富士教育出版社
レベル：基本～標準（★☆☆）
特徴：

中学入試対策用として作成された単元別の基本問題集。割合に関する基本事項の確認から標準レベルまでの問題で構成。
Amazonより引用

『中学受験算数・東大卒プロ家庭教師がやさしく教える「割合」キソのキソ改訂3版』

中学受験算数・東大卒プロ家庭教師がやさしく教える「割合」キソのキソ改訂3版 (YELL books)

出版社：エール出版社
レベル：基本～標準（★☆☆）
特徴：

「割合」を制するものが中学受験算数を制する。割合を苦手とする生徒に楽しく成績を伸ばす秘訣を伝授。
Amazonより引用

『Step by step 受験算数比・割合の線分図攻略法』

線分図を使って解く比・割合の問題がまとめられています。あれこれ勉強してこんがらがってきた頃に復習用として使うのがおすすめです。

Step by step 受験算数比・割合の線分図攻略法

出版社：文芸社
レベル：標準（★★☆）
特徴：

中学受験において頻出である比・割合の線分図。特に中堅校以上の私立中学・国立中学などでは、必出といっていい。今から線分図に取り組むという人も、今まで線分図を習ってちょっとわかりにくいという人も、試行錯誤しながらでも必ず習得できるように、大判で実際に書き込みをしながら学べるなど、既存の学習参考書よりも工夫して書かれた参考書。
Amazonより引用

『中学入試分野別集中レッスン算数文章題』

割合に限定されているわけではありませんが、文章題全般の学習用に便利です。

中学入試分野別集中レッスン算数文章題 (中学入試分野別集中レッスン)

出版社：文英堂
レベル：基礎～標準（★☆☆）
特徴：

弱点克服が中学入試突破の最大のカギ!
「苦手」分野を「短期間」で「集中ケア」する問題集!
【1】文章題の解き方・コツが短期間で身につく!
文章題の問題に特化して掲載しているので、
効率的に点数をアップさせることができます。
【2】例題・ポイントで確認,練習問題で定着!
例題とポイントで学習内容やコツを確認し、
書き込み式の練習問題に取り組むことで、
ひとりで解ける力がつきます。
【3】丁寧な解説で,着実にレベルアップ!
正しい解法が身につくように、
例題と練習問題には丁寧な解説を載せているので、
中学入試算数の考え方・解き方をしっかり学習できます。
Amazonより引用

ほかの科目の問題や解き方のコツ

ほかの科目の勉強方法や問題を下記の記事で案内しています。ぜひ、ご覧ください。

【算数】

割合の解き方
　中学入試によく出る割合の問題
 比の解き方
　中学入試によく出る比の問題
 速さの解き方
　中学入試によく出る速さの問題
 平面図形・空間図形の解き方

【国語】

【中学受験】国語の勉強法と入試出題傾向を解説
 【中学受験】国語長文読解を短期間で伸ばす勉強法
 記述問題の書き方と勉強方法
 おすすめの記述・作文問題集

【理科】

【中学受験】理科を得意にできる勉強方法
 【中学受験】理科のおすすめ問題集
 中学入試の理科によく出る問題の一問一答
 中学入試理科でよく出る問題の語呂合わせ一覧
 中学受験の理科でよく出る記述問題
 中学入試の理科でよく出る計算問題の公式一覧とおすすめの計算問題集

【社会】

【中学受験】社会で貯金を20点つくる勉強法を紹介
 中学入試の社会によく出る問題の一問一答
 中学受験の社会によく出る年号・年代の語呂合わせ
 【中学受験】歴史の流れを時代別に解説
 【中学受験】社会のおすすめ問題集

まとめ

いかがでしょうか。

中学受験生向けに、割合の解き方のコツを紹介しました。

割合は中学受験で最重要と言っていいほど大切な単元です。

勉強の難易度が本格化する5年生から苦手になる子が激増することがわかっています。

ですが、解き方のコツをつかんで練習すれば間違いを劇的に減らせます。

現在算数を苦手にしている人は、自分にはそれだけ伸びしろがあるんだと考えるようにしてみてください。

今は苦戦しているかもしれませんが、大きな伸びしろがあるということは、逆転合格できる可能性もたかいです！

ぜひ自信をつけて、積極的に算数をモノにしていきましょう！

また、特定の単元でどうしても詰まってしまう場合は、家庭教師をスポット的に利用すると便利です。