「一次関数の文章題の解き方が分からない」
このように、一次関数のなかでも文章題をはじめとする応用問題を苦手にしている中学生は多いです。
定期テストで90点台を目指す人は解けるようになっておきたい問題ですし、高校入試でも必ず出る問題です。
そこで、中学生向けに一次関数の利用の解き方のコツを解説し、練習問題を用意しました。
一次関数の利用をマスターし、テストで高得点をねらいましょう!
※関連記事:一次関数とは何かを分かりやすく解説
一次関数とは何か

一次関数の基本
一次関数は、y=ax+bの式で表す関数で、「a」は直線の傾きを、「b」はグラフがy軸と交わる点(切片)を表します。
xの値が増加または減少するにつれてyの値が比例して変化します。
傾き(変化の割合)や切片については、以下の記事でくわしく解説しています。
一次関数の傾きと切片の求め方(公式)を分かりやすく解説(練習問題あり)【中学数学のテスト対策】
一次関数の変化の割合とは(中学生):変化の割合の求め方を解説(変化の割合を求める練習問題つき)
一次関数のグラフと特徴
一次関数のグラフは直線になります。傾きaは「直線がどれだけ傾いているか」を示し、値が正なら右上がり、負なら右下がりです。
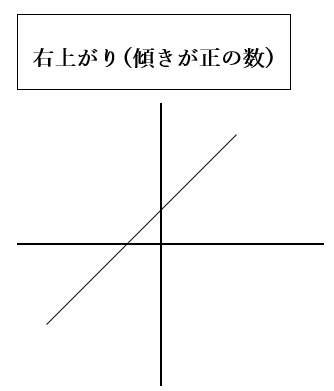
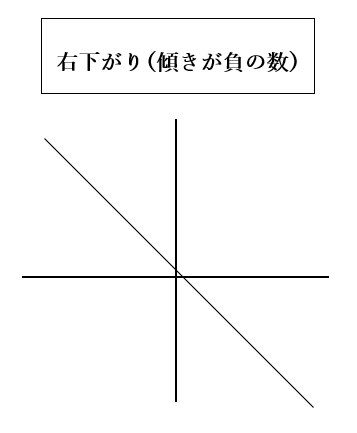
切片 bbb はy軸との交点を表し、例えば y=2x+3y = 2x + 3y=2x+3 の場合、切片は3、傾きは2です。傾きは、2点間のy差をx差で割ることで計算できます。
まとめ
- 一次関数の基本の式:y=ax+b
- グラフの特徴:傾きaは直線の傾きぐあい、切片bはy軸との交点
- 計算ポイント:傾きは(yの増加量)/(xの増加量)で求める
一次関数の利用の解き方のコツ

一次関数の利用の問題は図形や長い文章が出てくるため、むずかしく感じます。
解き方のコツを紹介します。
参考:【数学】 実践事例:中学校2年生 /実施機関:京都市教育委員会
y=ax+bの式をつくる
まず、y=ax+bの式をつくりましょう。これは利用の問題にかぎらず、変化の割合やグラフの問題など一次関数全般で役立つ方法です。
※関連記事:一次関数のグラフ:グラフのかき方、グラフの読み方の説明とグラフの練習問題
y=ax+bの式にxやyの値を代入する
一次関数の問題では、問題文で何をx、yにするか決められているものがよくあります。そうした問題では、y=ax+bの式にxやyの組み合わせを代入してa、bの値を求めましょう。
y=2x+3のように、式さえ完成させれば問題を解きやすくなります。
何をxとyにするか決まっていない問題ではxを先に決める
一次関数の問題のなかには、何をxとyにするかが書かれていないものもあります。何をxで何をyにするかを自分で決めないといけません。
以下の手順で決めましょう。
- もとにする値をxにする
- xが変わると自動的に値が変わるものをyにする
メインになるのはxです。xは変化の割合とも呼び、変化の割合が一次関数のおおもとになる数字です。
※変化の割合については、以下の記事でくわしく解説しています。
一次関数の変化の割合の求め方と練習問題
問題文を読んで、「もとになる値はどれかな?」と探してみましょう。
例えば、「あるばねに10gのおもりを下げると20cmになり、30gのおもりを下げると25cmになった。」という問題で考えてみます。
この問題では、「ばねの長さ」と「おもりの重さ」という2種類の数字が出ています。
この場合、「おもりの重さ」が「もとになる数字」です。おもりの重さを変えるとばねの長さが変わるからです。ばねの長さを変えるとおもりの重さが変わるわけではありません。
このように、一次関数の問題では大抵2種類の数字が提示されているので、「どちらがもとになる数字かな」と考え、もとになるほうをxにします。
一次関数の文章問題のパターン別の解き方
一次関数の文章問題はいくつかのパターンに分かれています。パターン別に解き方を解説します。
問題文にxとyが出てくる問題
まず多いのが、問題文中でxとyを何にするかが決められているパターンです。
例えば以下のような問題です。
「あるばねにxgのおもりを下げたときのばねの長さをxcmとする。10gのおもりを下げると20cmになり、30gのおもりを下げると25cmになった。ばねの長さが40cmになるのは、何gのおもりを下げたときか。」
解き方
前述のように、まずy=ax+bの式をつくります。このパターンの問題では何をxとyにするかが決まっているので、xとyのセットをy=ax+bに代入します。
問題文をみると、以下の2種類の手順が書かれています。
これらに書かれている数字をx、yに変えると以下の組み合わせができます。
それぞれy=ax+bに代入すると、以下の2つの式ができます。
この2つの式を連立方程式にして解きます。
時間で値が変わる問題
時間が変化するともう一方の数値が変化する問題パターンも出てきます。例えば、以下のような問題です。
「AさんはBさんとプレイランドに行きました。入場料が1000円で、1時間あたり500円ずつ料金が加算されます。1人2000円以内で遊ぶには、何時間以内で退場すればいいですか。」
解き方
時間が変化する問題では以下のようにxとyを決めます。
前述の問題を例にして解き方を説明します。
「AさんはBさんとプレイランドに行きました。入場料が1000円で、1時間あたり500円ずつ料金が加算されます。1人2000円以内で遊ぶには、何時間以内で退場すればいいですか。」
遊ぶ時間をx、料金をyにしてy=ax+bの式をつくります。
入場料1000円とあるので切片が1000、
1時間あたり500円とあるので変化の割合が500だと分かります。
これをy=ax+bの式に代入すると、y=500x+1000になります。
問題では「1人2000円」とあるので、y=2000をy=500x+1000に代入して、「x=遊ぶ時間」を求めます。
このように、xやyが設定されていない問題で「時間の変化」が関係する場合、時間をxに置きましょう。
速さの問題
速さの問題はよく出てきます。2パターンあります。
それぞれのパターンの解き方を説明します。
すれちがうパターンの解き方
2人の人間や電車などが別々の場所を出発し、それぞれの目的地までの途中ですれちがう問題です。
このパターンの問題では、「どこで/いつすれちがうか」を求めましょう。
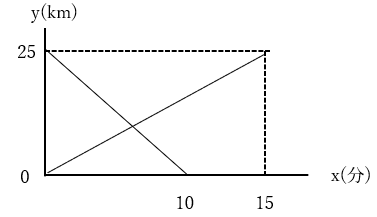
「ある人がA町から25kmはなれたB町へ出発した。同じ時刻にB町からバスがA町に向かって出発した。この人がA町を出発してから10分後にバスとすれちがった。x分後のA町からの距離をykm、A町を出発してからの時間をx分とする。このとき、バスとすれちがったのはA町から何kmの地点か求めよ。」
図をみると、2本の直線が引かれています。この2本の直線が交わる点が「すれちがった地点」です。
ある人の一次関数のグラフとバスの一次関数のグラフを式にして、連立方程式にして計算すると解けます。
まずy=ax+bの式をつくります。が、0からの出発なのでbは0と考えます。
図をみると、25kmはなれた距離をある人は15分で移動し、バスは10分で移動しています。
すると、それぞれの式は以下のようになります。
この2つの式を連立方程式にして計算します。
途中で休けいする問題の解き方
もうひとつが、途中で休けいしたり、別の場所に立ち寄ったりするパターンです。
休けいする前と休けいした後で移動速度が変わることがよくあります。必要に応じて、休けいする前・休けいした後の2種類の式をつくります。
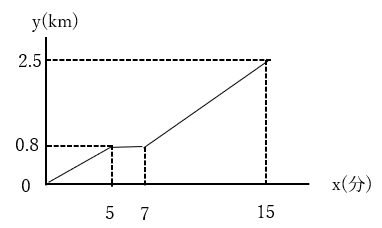
「ある人が自宅から図書館に向けて出発した。途中で知り合いにあって2分立ち話をした。上記の図は、この人が自宅を出発してからx分後の自宅からの距離をykmとして、xとyの関係を表したものです。もし立ち話をせずに、自宅を出発したときの速さで図書館まで移動したとしたら、何分で到着していたか。」
まず、y=axの式をつくります。出発したときにはy=0なので、切片は0です。
図を見ると、出発してから5分後の時点で0.8kmまで進んでいます。そのため、y=axの式にx=5、y=0.8を代入します。
y=ax
0.8=5a
a=4/25
これで、出発してから5分後までの速さは「y=4/25x」で表せると分かりました。
問題では、この速度で2.5kmの地点まで行くのに何分かかるかを問われています。そこで、y=4/25の式にy=2.5を代入します。
2.5=4/25x
x=125/8(分)
点Pが動く問題(動点の問題)
動点の問題(点Pが動く問題)も一次関数の利用で定番です。
長方形や正方形の辺上を点Pが動き、面積をy、時間をxにする問題です。
解き方
動点の問題では点Pがどの辺にいるかを確認しましょう。
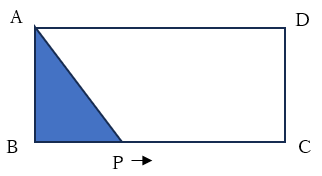
「長方形ABCDがある。辺ABは6cm、辺BCは14cmである。
点PがBを出発して毎秒1cmずつの速さでB→C→Dと移動する。
点PがBからxcm動いたときの△ABPの面積をycm2とする。
点Pの面積が最初に30cm2になるのは、Bを出発して何秒後か。」
前述のように、まず点Pがどの辺にいるときのことを問われているかを確認します。「面積が最初に30cm2になるとき」なので、点Pが辺BC上にあるときだと分かります。
そこで、点Pが辺BC上にあるときのxとyの関係を表す式をつくります。ひとまず、y=axです。
xとyの組み合わせをy=axの式に代入するのですが、xとyの値を何にすれば良いか分からないときは、x=1、x=2、x=3のときのyの値を示す表をつくると分かりやすいです。
| x(cm) | 1 | 2 | 3 | 4 |
| y(cm2) | 3 | 6 | 9 | 12 |
表をみると、x=1のときy=3になります。この組み合わせをy=axに代入します。
すると、a=3となり、y=3xという式が出来上がります。
面積(y)が30cm2になるときの時間(x秒)を知りたいので、
30=3x
x=10(秒)
一次関数の利用の練習問題
それでは、一次関数の文章問題を解いて練習してみましょう。
問題(1)
長さ24cmのろうそくがあります。このろうそくに火をつけると1時間後に19cmになりました。
①ろうそくが燃えつきるのは、火をつけてから何時間何分後ですか。
②ろうそくの長さが3cmになるのは、火をつけてから何時間何分後ですか。
解答
まず、xとyを何にするかを決めます。
この問題では、「ろうそくの長さ」と「火をつけからの時間」が出ています。「火をつけてからの時間」がもとになる数字なのでこれをxにし、「ろうそくの長さ」をyにして、y=ax+bの式をつくります。
また、ろうそくの長さは火をつけるまえは24cmで、火をつけると短くなっていきます。ですので、y=ax+24だと分かります。
さらに問題文をみると1時間後に19cmになったとあるので、x=1、y=19を代入します。
すると、y=-5x+24という一次関数の式が完成します。
①4時間48分後
「ろうそくが燃えつきる」ということは、y=0になるとき。y=-5x+24にy=0を代入します。
するとx=24/5。
②4時間12分後
y=-5x+24にy=3を代入します。するとx=21/5。
問題(2)
ある電話会社には、以下の表のようにA、B2種類の料金プランがあります。1か月にx分通話したときの料金をy円とすします。
| 1か月の基本使用料 | 1分あたりの通話料 | |
| Aプラン | 1000円 | 50円 |
| Bプラン | 1500円 | 30円 |
①Aプラン、Bプランについて、yをxの式で表してください。
②BプランのほうがAプランより安くなるのは、1か月の通話時間が何分より長いときですか。
解答
①Aプラン:y=50x+1000、Bプラン:y=30x+1500
まずy=ax+bの式をつくり、Aプラン、Bプランそれぞれのxとyの組み合わせを代入します。
Aプラン:y=ax+1000に、x=1、y=1050を代入→a=50
Bプラン:y=ax+1500に、x=1、y=1530を代入→a=30
②25分より長いとき
まず、AプランとBプランで同じ料金になる通話時間を求めます。Bプランのほうが安くなるのは、その通話時間よりも長くなったときです。
①で求めた両方のプランの式を連立方程式にして計算します。
問題(3)
ある人がA町から20kmはなれたB町へ出発しました。この人がA町を出発してから5分後にB町からバスがA町に向かって出発しました。以下の図はこの人がA町を出発してからx分後のA町からの距離をykmとして、xとyの関係を表したものです。
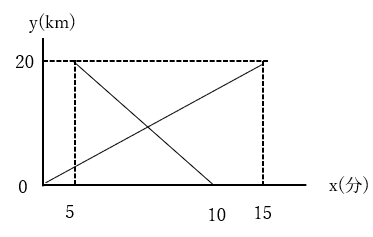
①この人がA町からB町へ移動する際のxとyの関係を式で表してください。
②この人とバスがすれちがったのは、バスがB町を出発してから何分何秒後ですか。
解答
①y=4/3x
原点を通っているので、まずy=axの式をつくります。さらに(15, 20)を通っているので、y=axにx=15、y=20を代入して計算します。
②7分30秒後
バスの移動について、yをxの式で表します。バスは(5, 20)と(10, 0)の2点を通っているので、y=ax+bにそれぞれ代入して連立方程式にして求めます。すると以下のような式になります。
y=-4x+40
この式と①で求めた式を連立方程式にして計算します。すると、x=15/2と出ます。
問題(4)
図のように、一辺が8cmの正方形ABCDがあります。点PはAを出発して辺上をB、Cを通ってDまで移動します。点PがAからxcm動いたときの△APDの面積をycm2とします。
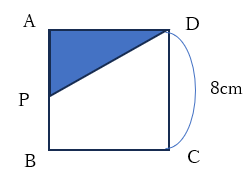
①点Pが辺AB、辺BC、辺CD上を動くとき、yをxの式で表してください。
②△APDの面積が最大になるのは、xの変域がどのようになるときですか。
解答
①辺AB:y=4x、辺BC:y=32、辺CD:y=-4x+32
点Pが辺AB上を動くときの図は以下のとおりです。三角形の面積は底辺×高さ×1/2です。
底辺(辺AD)は8cmで、点Pが移動するたびに高さ(辺AP)が長くなっていきます。
これを式にすると、y=1/2×8×xとなります。
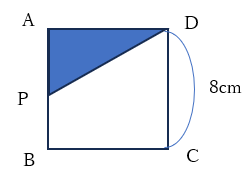
点Pが辺BC上を動くときの図は以下のとおりです。底辺(辺AD)は8cmで、高さ(辺AP)もずっと8cmです。xが増加してもyはずっと32なので、y=32です。
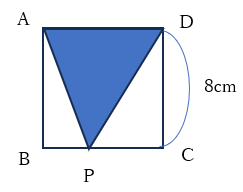
点Pが辺CD上を動くときの図は以下のとおりです。
三角形の面積は底辺×高さ×1/2です。底辺(辺AD)は8cmで、点Pが移動するたびに高さ(辺CD)は8cmから短くなっていきます。
Y=1/2×8×(8-x)
y=-4x+32
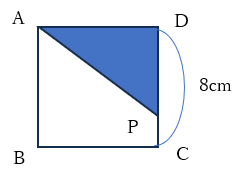
②8≦x≦16
①より、△APDの面積は最大32cm2で、点Pが辺BC上にあるときでした。
問題(5)
深さ75cmの直方体の空の水そうに、水道管2本を使って水を入れることにした。水道管1本だと毎分1.5cmずつ水面が高くなる。最初の8分間は水道管を2本使い、その後は水道管1本を使い、満杯になるまで水を入れた。水を入れ始めてからx分後の水面の高さをycmとする。
①はじめの8分間について、yをxに式で表してください。
②8分後から満水になるまでの間について、yをxの式で表し、xの変域も答えてください。
③水を入れ始めてから20分後の水面の高さを求めてください。
解答
①y=3x
水道管1本で毎分1.5cmずつ水面が高くなるので、水道管2本だと毎分3cmずつ水面が高くなります。このことから8分後までのxとyの関係を表にすると、以下のようになります。
| x(分後) | 0 | 1 | 2 |
| y(cm) | 0 | 3 | 6 |
x=0のときy=0で、x=1のときy=3になります。ここから式をつくります。
②8≦x≦34
①で求めたy=3xの式にx=8を代入すると、8分後の水面の高さが24cmと分かります。
8分後からのxとyの関係を表にすると、以下のようになります。
| x(分後) | 8 | 9 | 10 |
| y(cm) | 24 | 25.5 | 27 |
Xが1増えるごとにyは1.5ずつ増えているので、
y=1.5x+24
また、水面の高さは最大75cmなので、この式にy=75を代入してxの最大値を求めます。
y=1.5x+24
75=1.5x+24
x=34
③54cm
20分後なので、y=1.5x+24の式にx=20を代入します。(もし8分後以内なら、y=3xの式に代入します)
y=1.5x+24
y=30+24
y=54
中学数学の問題集(基本~応用レベル)
最後に、中学数学のおすすめ問題集を紹介します。
『中学10分間復習ドリル 数学2年』
数学を基本からコツコツ復習したい人に向いているドリルです。
1日10分から基本問題の演習ができます。

中学10分間復習ドリル 数学2年:サクサク基礎トレ! (受験研究社)
出版社:増進堂・受験研究社
『中学2年 数学 標準問題集』
基本レベルから応用レベルまで幅広く演習できる問題集です。
定期テストで平均点前後からスタートして90点くらいまでを目指せます。

中学2年 数学 標準問題集: 中学生向け問題集/定期テスト対策や高校入試の基礎固めに最適! (受験研究社)
出版社:増進堂・受験研究社
まとめ
いかがでしょうか。
中学生向けに、一次関数の利用(文章問題)の解き方をパターン別に解説し、練習問題を用意しました。
一次関数の文章題は速さ(すれちがう、休けいする)、水量、動点の問題などがよく出てきます。いずれの問題も一次関数の式をつくることと変化の割合を中心にすることが解法のポイントです。
コツをつかんで定期テストや高校入試で高得点をねらいましょう!



コメント