一次関数を苦手に感じる中学生は多いです。
変化の割合、傾き、切片、変域といった用語がいくつも出てくるうえに、問題の種類も多いのでややこしくなってきます。
ですが、一次関数の後に二次関数を習うため、一次関数を得意にしておくと二次関数も得意になりやすいです。
そこで、中学生向けに一次関数の基本的な内容（変化の割合、傾き、切片、変域の説明）や問題の解き方を解説し、練習問題を用意しました。
一次関数を得意にして、定期テストや高校入試の数学で高得点をねらいましょう！
※関連記事：比例・反比例の解き方
【下記は難関高校受験に強いZ会のHPへのリンクです。リンク先で資料請求ができます。】
Z会 中学生コースの案内
※Z会について下記記事でくわしく紹介しています。
【中学生向け】Z会タブレットコースの進め方：成績上位を取って難関校に合格する方法を解説
一次関数とは何か
関数とは、「2つの数字があり、一方の数字（x）が変化すると、それにあわせてもう一方の数字（y）も規則的に変化すること」です。
そのなかで、一次関数は「一次式の関数」です。
xが決まるとyも決まる場合、「yはxの関数である」と言います。
一次関数の公式
一次関数は以下の公式で表します。
y=ax+b
aやbに入る数字は問題によって変わります。
例えばa=2、b=1の場合、以下のような式になります。
y=2x+1
この式をもとに、xやyの値を求めます。表にすると以下のようになります。
| x | -2 | -1 | 0 | 1 | 2 |
| y | -3 | -1 | 1 | 3 | 5 |
一次関数の変化の割合（＝傾き）
一次関数の式にある「a」というのは「変化の割合」と呼びます。
「xが1増えるごとにyがどのような割合で変化するか」を表しています。
例えばa=3なら、「xが1増えるとyは3増える」という意味です。
変化の割合の求め方
変化の割合は「yの増加量/xの増加量」で求めます。
例えばxの増加量が3でyの増加量が6なら、
6÷3＝2で、変化の割合は「2」になります。
変化の割合と傾きは同じ意味
一次関数には「傾き」という用語も出てきます。これは変化の割合と同じ意味です。
つまり、y=ax+bという式の「a」は「変化の割合」であり「傾き」とも言います。
傾きがプラスなら右肩上がりのグラフ、マイナスなら左肩下がりのグラフになる
一次関数のグラフは傾きや変化の割合がプラス（2とか4とか）なら右肩上がりになります。
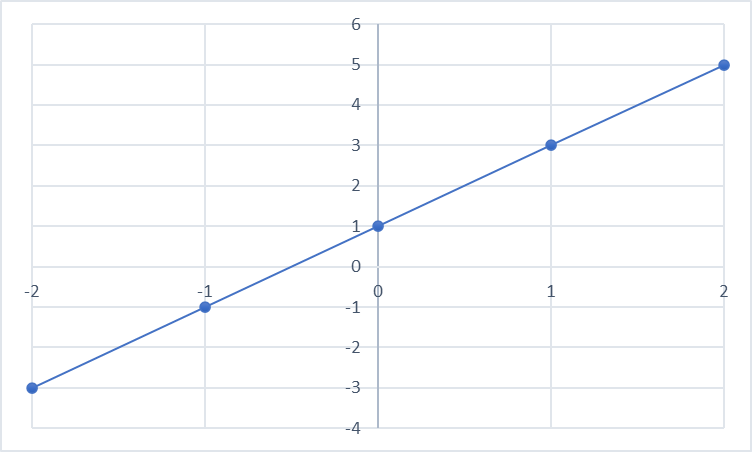
また、傾きや変化の割合がマイナス（-2とか-4とか）ならグラフは右肩下がりになります。
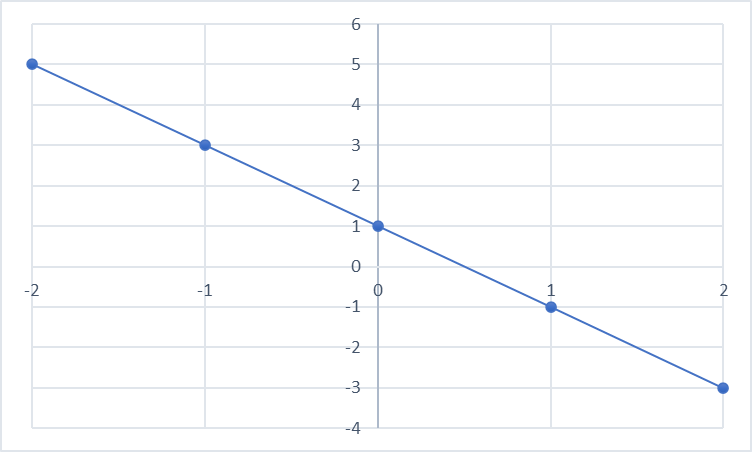
傾きや変化の割合がマイナス（-2とか-4とか）なら右肩下がりのグラフになります。
※関連記事：一次関数のグラフ：グラフのかき方、グラフの読み方の説明とグラフの練習問題
一次関数の切片
一次関数の式にある「b」は「切片（せっぺん）」と呼びます。
以下の図で、y軸上の点が切片です。
グラフを描くときは切片からはじめる
一次関数のグラフを描くときは、切片から描き始めると描きやすいです。
一次関数のグラフは直線なので、2つの座標を真っすぐの線で結べば完成です。2つの座標のうち1つを切片にすればズレずに描けます。
一次関数の変域
一次関数には「変域」という言葉が出てきます。変域とは「範囲」です。
xの変域：xがいくらからいくらまで変化するか
yの変域：yがいくらからいくらまで変化するか
例えば「xの変域が3から5まで」の場合、以下のように書きます。
3≦x≦5
≦は「しょうなり・イコール」と読みます。
変域の求め方
一次関数ではxの変域を求めよといった問題が良く出てきます。
前述のように変域は「3～5」「4～12」のような「数字の範囲」です。xが3～5のときや4～12のときにyはいくらからいくらになるかを求めます。
求め方はシンプルで、最小値と最大値を一次関数の式に代入するだけです。
「y=2x+1の式で、xの変域が3から5まで」となっていれば、x=3とx=5をy=2x+1に代入します。
x=3の場合
y=2×3+1
y=7
x=5の場合
y=2×5+1
y=11
上記のような計算結果になったので、yの変域は「7≦y≦11」となります。
一次関数の解き方
一次関数の問題は種類が多く、専門用語も出てくるためややこしくなってしまう中学生が多いです。
解き方を説明します。
一次関数の式をつくる
一次関数の問題が出てきたら、まず一次関数の式（y=ax+b）をつくりましょう。
yをxの式で表しなさい、変化の割合を求めなさい、グラフをかきなさいといったさまざまな種類の問題がありますが、ほとんどの問題は一次関数の式に数字を代入するところからはじめます。
ですので、何はともあれy=ax+bの式を問題用紙の余白やノートに書きましょう。
グラフをフリーハンドでかけるようにする
一次関数のグラフを、定規を使わずにフリーハンドでかけるようにしましょう。
グラフがかかれている問題もあれば、かかれていない問題もあります。グラフのない問題でも、数値変化の様子をイメージしやすくなるように自分で問題用紙の余白などにかいておきましょう。
上記のような、サラっとしたもので十分です。右肩上がりなのが右肩下がりなのかが分かり、x軸やy軸のどの辺をとおるのかを大まかにイメージできれば十分です。
用語の意味を覚える
一次関数には変化の割合、傾き、切片、変域といった用語がいくつも出てきます。
これらの言葉の意味が分からないと問題文を読んでも「何をしなさいと指示されているのか」が分かりません。
用語を自分でも説明できるまで覚えておきましょう。
具体的な数字をy=ax+bに入れて計算する
ほとんどの問題では変化の割合、傾き、切片、xの値、yの値のいずれか1つ以上が書かれています。その数字をy=ax+bの式に入れて計算しましょう。
例えば、「傾きが3で切片が2の一次関数の式で、x=3のときyの値を求めなさい。」のように出題されます。
傾きが3、切片が2とあるので早速y=ax+bに代入します。a=傾き＝3で、b=切片＝2です。以下のようになります。
y=3x+2
「x=3のとき」とあるのでさらにこの式にx=3を代入します。
y=3×3+2
y=11
すると、y=11という計算結果になりました。答えはy=11です。
このように、y=ax+bという式をつくり、その式に「値が分かるもの」を入れて計算します。
連立方程式の計算を練習する
一次関数では連立方程式の計算をして答えを求める問題も出てきます。代表的なものは下記の2パターンです。
この解き方は応用問題でもよく使うので、数学の定期テストで平均点以上を取りたい人や難関校を志望している人は「必ず」連立方程式の計算を練習して得意にしておきましょう！
一次関数の練習問題
それでは、一次関数の練習問題を解いて、解き方をマスターしましょう。
問題(1)
時速4kmでx時間歩いたときの道のりをykmとする。
①yをxの式で表してください。
②3時間歩くと、何km歩いたことになりますか。
③24kmの道のりを歩くのに何時間かかりますか。
解答
①y=4x
②12時間
y=4xの式にx=3を代入する
③6時間
y=4xの式にy=24を代入する
問題(2)
次の一次関数について、［ ］のようにxの値が増加するときの変化の割合を求めてください。
①y=-2x+3［-2から4まで］
②y=3x+2［-5から7まで］
③y=-3x-4［3から8まで］
解答
変化の割合はy=ax+bのaの位置にある数字なので、xがどのように変化していてもaの位置にある数字を答えれば良い。
①-2
②3
③-3
問題(3)
一次関数y=2x+4で、次の場合のyの増加量を求めてください。
①xの増加量が2のとき
②xの増加量が5のとき
③xの増加量が-3のとき
解答
変化の割合＝yの増加量/xの増加量なので、
yの増加量は「xの増加量×変化の割合」で求められる。
①4
xの増加量が2で変化の割合が2
②10
xの増加量が5で変化の割合が2
③-6
xの増加量が-3で変化の割合が2
問題(4)
次の直線の傾きと切片を答えてください。
①y=3x-2
②y=7x+1
③y=-2x-5
解答
y=ax+bで傾きはaの位置にある数字で、切片はbの位置にある数字。
①傾き：3、切片：-2
②傾き：7、切片：1
③傾き：-2、切片：-5
問題(5)
次の一次関数のグラフをかいてください。
①y=2x+2
②y=-3x+1
③y=1/2x+3
解答
x座標、y座標ともに整数になる点を直線で結びます。線がずれないように気を付けましょう。（以下の解答は許容範囲内ぎりぎりくらいです。）
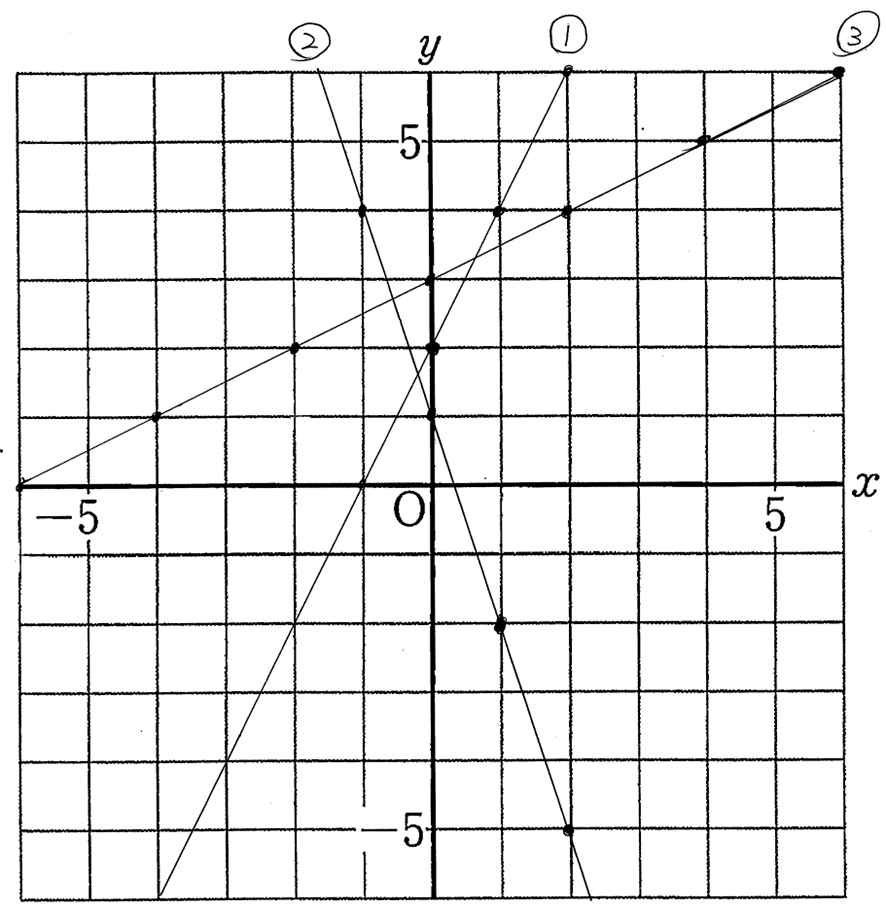
問題(6)
次の一次関数について、xの変域が［ ］であるときのyの変域を求めてください。
①y=2x+3［-3≦x≦5］
②y=-3x+1［2≦x≦6］
③y=2x-3［-2≦x≦3］
解答
①-3≦y≦14
y=2x+3にx=-3、x=5をそれぞれ代入する。
x=-3のとき、y=-3
x=5のとき、y=14
②-5≦y≦-17
y=-3x+1にx=2、x=6をそれぞれ代入する
x=2のとき、y=-5
x=6のとき、y=-17
③-7≦y≦3
y=2x-3にx=-2、x=3をそれぞれ代入する
x=-2のとき、y=-7
x=3のとき、y=3
問題(7)
グラフが次のようになる一次関数の式を求めてください。
①点（0, 2）を通り、傾きが2の直線
②点（-3, 3）を通り、傾きが3の直線
③点（2, 6）を通り、y=2xのグラフに平行な直線
④変化の割合が3で、x=2のときy=7の直線
⑤xの値が1ずつ増加するとyの値が2ずつ減少し、x=3のときy=-2の直線
⑥2点（-2, 4）（3, 19）を通る直線
⑦2点（-1, 4）（2, -2）を通る直線
⑧2点（1, 4）（2, 3）を通る直線
⑨x=0のときy=3、x=4のときy=11
⑩x=2のときy=1、x=6のときy=-7
解答
まず、y=ax+bの式をつくり、aとbに何か数字を入れられれば完成です。傾き/変化の割合＝aで、切片＝b。
①y=2x+2
（0, 2）はy軸上の点なので、切片が2と分かる。傾きが2なので、y=2x+2。
②y=3x+12
傾きが3なので、y=3x+b。この式にx=-3、y=3を代入してbの値を求める。
③y=2x+2
平行というのは、傾きが同じということ。y=2xに平行なので、y=2x+bの式になる。
この式にx=2、y=6を代入してbの値を求める。
④y=2x+1
変化の割合が3なので、y=3x+bになる。この式にx=2、y=7を代入してbの値を求める。
⑤y=-2x+4
xの値が1増加するとyの値が2減少するということは、変化の割合が-2。
なので、y=-2x+b。この式にx=3、y=-2を代入してbの値を求める。
⑥y=3x+10
y=ax+bの式にx=-2とy=4、x=3とy=19それぞれ代入する。すると、以下の2つの式ができる。
4=-2a+b
19=3a+b
この2つの式を連立方程式にしてxとyを求める。
⑦y=-2x+2
y=ax+bの式にx=-1とy=4、x=2とy=-2それぞれ代入する。すると、以下の2つの式ができる。
4=-a+b
-2=2a+b
この2つの式を連立方程式にしてxとyを求める。
⑧y=-1/2x+4
y=ax+bの式にx=1とy=4、x=2とy=3それぞれ代入する。すると、以下の2つの式ができる。
4=a+b
3=2a+b
この2つの式を連立方程式にしてxとyを求める。
⑨y=2x+3
まずy=ax+bの式をつくる。x=0のときy=3なので、b（切片）は3。y=ax+3。
y=ax+3の式にx=4とy=11を代入してaを求める。
⑩y=-x+3
y=ax+bの式にx=2とy=1、x=6とy=-7それぞれ代入する。すると、以下の2つの式ができる。
1=2a+b
-7=6a+b
この2つの式を連立方程式にしてxとyを求める。
問題(8)
傾きが3で、点（2, 4）を通る直線が点（-3, m）を通るとき、mの値を求めてください。
解答
答え：-11
まず、y=ax+bの式をつくる。傾きが3なので、y=3x+b。
この式にx=2、y=4を代入してbを求める。すると、y=3x-2になる。
y=3x-2にx=-3を代入して、x=-3のときのy座標（m）を求める。
問題(9)
傾きが-2で、点（3, 1）を通る直線が点（-2, m）を通るとき、mの値を求めてください。
解答
答え：11
まず、y=ax+bの式をつくる。傾きが-2なので、y=-2x+b。
この式にx=3、y=1を代入してbを求める。すると、y=-2x+7になる。
y=-2x+7にx=-2を代入して、x=-2のときのy座標（m）を求める。
問題(10)
3点（1, 2）、（4, 8）、（6, m）が一直線上にあるとき、mの値を求めてください。
解答
答え：12
まず、y=ax+bの式をつくる。x=1のときy=2になり、x=4のときy=8になるので、それぞれy=ax+bに代入する。
すると、y=2xになる。
y=2xにx=6を代入して、m=12
【別解】
(1, 2)（4, 8）より、傾きを求める。
(8-2)/ (4-1)=2
y=2x+bにx=1、y=2を代入すると、b=0と分かるので、y=2x。以下は同じ解き方。
問題(11)
Aさんの家から駅まで1400m離れており、家と駅の間に本屋がある。Aさんが家を出発してから4分後に本屋に立ち寄り、それから10分後に本屋を出発して駅まで歩いた。出発してからx分後の地点から駅までの距離をymとする。
| x | 4 | 14 | 26 |
| y | 1080 | 1080 | 0 |
①家から本屋に行くまでの速さと、本屋から駅まで行く速さはどちらのほうが速かったでしょうか。
②Aさんが家を出てから20分後には、駅まで残り何mですか。
解答
①本屋から駅まで行く速さ
家から本屋まで4分間で1400-1080=320m進んでいる。つまり、320m÷4分＝80m/分。
同様に、本屋から駅まで12分間で1080m進んでいる。つまり、1080m÷12分＝90m/分。
②540m
「家を出発してから20分後」は「本屋を出発してから6分後」。
本屋から駅まで90m/分で歩いたので、6分間で90×6=540m歩いたことになる。
1080m-540m=540m
問題(12)
深さ80cmの水そうがあります。この水そうに水を入れ始めてから5分後に別の蛇口からも入れはじめたところ、15分で水そうは満杯になりました。
水を入れはじめてからの時間をx分、水そうの深さをycmとし、xとyの関係を表にすると以下のようになりました。
| x（分） | 5 | 10 | 15 |
| y（cm） | 20 | 50 | 80 |
①5分後までのxとyの関係を式で表し、5分後から15分後までのxとyの関係も式で表してください。
②最初から2つの蛇口から水を入れていたら、水そうは何分で満杯になっていましたか。
解答
①5分後まで：y=4x、5分後から15分後まで：y=6x+20
まず、y=axの式をつくる。
5分後まで：y=axの式にx=5、y=20を代入する。
→ y=4x
5分後の時点で20cmまで水が入っているので、y=ax+20の式をつくる。
5分後から10分後まででxは5増加し、yは30増加しているので、
y=ax+20の式にx=5、y=30を代入する。
→ y=6x+20
②
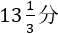
2つの蛇口から水を入れると変化の割合は6。水そうが空の状態から水を入れるので、y=6xの式になる。
この式にy=80を代入すると、
x=40/3
中学数学の問題集
最後に、中学数学のおすすめ問題集を紹介します。いずれもAmazonのリンクをつけています。
『中学10分間復習ドリル 数学2年』
数学を基本からコツコツ復習したい人に向いているドリルです。
1日10分から基本問題の演習ができます。
中学10分間復習ドリル 数学2年:サクサク基礎トレ! (受験研究社)
出版社：増進堂・受験研究社
『中学2年 数学 標準問題集』
基本レベルから応用レベルまで幅広く演習できる問題集です。
定期テストで平均点前後からスタートして90点くらいまでを目指せます。
中学2年 数学 標準問題集: 中学生向け問題集/定期テスト対策や高校入試の基礎固めに最適! (受験研究社)
出版社：増進堂・受験研究社
まとめ
いかがでしょうか。
中学生向けに一次関数の用語の意味や解き方を説明しました。変化の割合、傾き、切片の用語の説明や変域の求め方、一次関数のグラフのかき方など。
一次関数ではまずy=ax+bの式をつくり、文字に数字を入れて計算します。また、用語の意味をしっかり覚えたうえで練習問題で定着させましょう。基礎から応用までの練習問題も載せています。
【下記は難関高校受験に強いZ会のHPへのリンクです。リンク先で資料請求ができます。】
Z会 中学生コースの案内
※Z会について下記記事でくわしく紹介しています。
【中学生向け】Z会タブレットコースの進め方：成績上位を取って難関校に合格する方法を解説
コメント