PRを含みます

中学理科の計算問題と分かりやすい解説：酸化銅、密度、濃度、地震、質量、圧力、物体の運動、仕事など

中学生

2023.06.112025.11.08

中学理科のテストや入試で差がつくのは「計算問題」です。
「公式は覚えたのに間違える」「文章問題になるとわからない」――そんな悩みを持つ中学生は多いでしょう。

この記事では、中学理科の計算問題を分野別（物理・化学・地学・生物）にわかりやすく整理し、定期テストや入試でよく出る公式・例題・解き方のコツを徹底解説します。
初心者でも理解できるよう、図や例を交えながら「得点源に変える学習法」まで詳しく紹介。

計算問題を制する者が理科を制す！
苦手を克服して、テストで確実に点を取れる力を身につけましょう。

※関連記事：理科の一問一答問題

Z会　中学生コースの案内

※関連記事：【中学生向け】Z会タブレットコースの進め方

中学理科の計算問題とは？【出題傾向と勉強法のコツ】
中1理科の問題：密度の計算問題
中1理科の問題：水溶液の計算問題（濃度など）
中1理科の問題：音の速さを求める計算問題
中1理科の問題：地震の計算問題
中2理科の問題：化学変化と質量の計算問題（酸化と還元）
中2理科の問題：電流の計算問題
中2理科の問題：圧力の計算問題
中2理科の問題：水蒸気の計算問題（湿度、飽和水蒸気量など）
中3理科の問題：運動の速さの計算問題
中3理科の問題：仕事の計算
中3理科の問題：エネルギーの計算問題
分野横断で使える！中学理科の計算公式一覧表
1. 物理・化学・地学・生物の重要公式まとめ
2. 単位変換の早見表（cm³↔m³、g↔kg など）
テスト・入試対策の実践ステップ
おすすめの中学理科計算問題集
まとめ

中学理科の計算問題とは？【出題傾向と勉強法のコツ】

概要
中学理科の計算問題は、教科書で学ぶ概念（力、密度、濃度、化学反応、地震の波、遺伝の確率など）を数式や割合で扱う問題です。暗記だけでなく「公式の使い方」「単位処理」「文章から必要な数値を読み取る力」が重要になります。定期テストは「基本＋少し応用」レベル、入試や実力テストは「複数の考え方を組み合わせる応用問題」が出やすいです。

出題傾向（短く）

定期テスト：教科書レベルの公式をそのまま使う問題が多い。計算は短め。
学力テスト・入試：文章量が増え、複数工程（単位変換→式立て→計算→考察）を要求される問題が増える。
共通点：図表・グラフの読み取り＋計算を組み合わせる問題が増加。

勉強法のコツ（全体像）

公式と意味をセットで理解する（丸暗記は危険）。
単位変換に慣れる（g⇄kg、cm³⇄m³、mL⇄L）。
文章を数値化する練習（どの値が求める対象かを判断する）。
反復練習＋時間を決めた模擬演習（制限時間に慣れる）。
「解答プロセスチェックリスト」を作る（後述）。

計算問題が苦手な中学生が多い理由

主な原因と対処法

公式の意味を理解していない
- 原因：公式をただ丸暗記して代入だけしている。
- 対処法：公式がどこから来るか（関係性）を簡単に説明できるようにする。例：密度＝質量÷体積 → 「同じ体積なら質量が大きいほど密度が大きい」と言えるか。
単位変換ミスが多い
- 原因：単位を揃えずに計算してしまう。
- 対処法：問題を解く前に「全ての値の単位を確認・統一」する習慣をつける。覚え方：1000倍／1000分の1を表にしておく。
問題文の読み取り不足
- 原因：図や条件を飛ばして計算を始めてしまう。
- 対処法：問題を3回読む（1回：全体把握、2回：数値と条件の確認、3回：求めるものの再確認）。
途中計算を省略しすぎる／書かない
- 原因：頭の中で飛ばしてしまい、どこでミスしたか分からない。
- 対処法：途中式を必ず書く。部分ごとに単位も書くとミスが減る。
練習量不足／学習の偏り
- 原因：苦手分野を避けて練習しない。
- 対処法：苦手分野を週に数問必ず入れる「強制ルーティン」を作る。

ワンポイント：苦手の原因を紙に書き出し（例：「単位」「読み間違え」など）、個別に対策を立てると改善が早いです。

理科の計算問題が出る4分野（物理・化学・地学・生物）

それぞれの分野で「よく出る計算の種類」と「具体的な練習例」を示します。

物理

よく出る計算：密度、速度・時間・距離（中1から）、圧力、仕事・エネルギー（中2〜）、電流・電圧・抵抗（オームの法則、中2〜）
練習例：密度＝質量÷体積、v＝距離÷時間、P＝F÷S、W＝F×d、V＝IR
つまずきポイント：単位混同（gとkg、cmとm）／ベクトル的な理解（向きの扱い）

化学

よく出る計算：濃度（％、質量パーセント濃度・モルは高校だが基礎濃度）、化学反応での比（比例計算）、気体の体積比（入試で出る）
練習例：濃度＝（溶質の質量÷溶液の質量）×100、反応前後の質量保存の計算
つまずきポイント：溶液の分母を何にするか（溶媒か溶液か）／化学式の係数の扱い

地学

よく出る計算：地震波の到達時間から震源距離を割り出す、天体の見かけの運動や影の長さの計算、降水量や平均値の計算
練習例：S波・P波到達時間差から震源距離を推定する問題、影の比から太陽高度を求める問題
つまずきポイント：図の読み取り、複数条件を整理する力

生物

よく出る計算：光合成や呼吸での気体の増減の計算、遺伝の確率（優性・劣性の割合）、個体数変化の割合（簡単な比率）
練習例：親の遺伝子組み合わせから子の遺伝確率を求める（比と確率の基本）
つまずきポイント：確率の考え方の誤解（順列・組合せを混同する）

点数アップのコツ（公式暗記＋単位変換＋文章の読み取り）

ここは実践的なチェックリストとテクニックを示します。試験で即使えるものだけを厳選。

1）公式は「意味」とセットで覚える

ただ丸暗記するのではなく、なぜその形になるかを一文で説明できるようにする。
例：密度＝質量÷体積 → 「同じ体積なら質量が大きいほど密度が大きい」

2）単位変換は最初に必ずやる

解く前にすべての値の単位を揃える（例：g→kg、cm³→m³）。
簡単なルール表を作る：
- 1000 g = 1 kg
- 1000 mL = 1 L
- 100 cm = 1 m
なぜ重要か：単位が合っていないと答えが桁違いになる（致命的ミス）。

3）文章の読み取り：設問を3回読む

全体をざっと読む（何が問われている？）
数値と条件を拾う（図・単位も確認）
求めるものと解法の方針を決める（公式は何か？どの単位に揃えるか？）

4）解答プロセス（チェックリスト）

STEP1：求める量を明確に書く（例：「密度ρ」）
STEP2：使う公式を一つに定める（例：ρ＝m÷V）
STEP3：数値を単位を合わせて代入（途中式を省略しない）
STEP4：計算（電卓の使い方も練習）
STEP5：結果の単位を付け、妥当性を確認（桁、単位、常識値）
STEP6：もし時間があれば逆算で確認（元の値に戻せるか）

5）時間配分のコツ（テスト向け）

簡単そうな計算問題→最初にさっと解く（得点回収）。
応用問題→後回しにして「取れるところ」を確実に取る。
本番で迷ったら「単位チェック」→単位が合えば大抵は式が合っている。

6）練習方法（短期〜長期）

毎日 15〜30 分の計算問題（継続が鍵）。
週に1回は過去問や模擬問題で時間を計って解く。
間違いノートを作り、同じミスを3回で潰す。

入試でよく出る計算分野ランキング

入試や学力テストで頻出度が高い順に、理由と代表的な問題例（短文）を挙げます。※地域や年によって差はありますが、総合的な傾向に基づく一般的なランキングです。

1位：物理（運動・電気・密度・圧力）

理由：物理は公式ベースで出題しやすく、数値化された現象（速さ、力、電流等）が多数出題されるため得点源になりやすい。
代表問題例：ある箱が1.5 m進むのに3.0 sかかったときの速さを求めよ（速さ＝距離÷時間）。
対策：公式の意味を理解／単位変換を確実に／図を描いて問題を可視化

2位：化学（濃度・化学反応の比例・気体関係）

理由：溶液の濃度や化学反応の割合は定型問題が多く、計算パターンを覚えることで高得点が狙える。
代表問題例：100 g の溶液に溶質が10 g 含まれるときの質量パーセント濃度は何％か。
対策：分母（溶媒か溶液か）の扱いを整理／反応の割合は係数比に注意

3位：地学（地震・天体・気象の計算）

理由：図表や到達時間の差など「整理して計算する」問題が多く、図読み力と計算を組合わせる力が求められる。
代表問題例：P波とS波の到達時間差から震源までの距離を求める問題（速さ×時間差などの考え方）。
対策：図を正確に読み取る練習／単位と速さの関係を確認

4位：生物（遺伝の確率・物質の増減）

理由：生物の計算問題は他分野に比べると数は少ないが、遺伝の確率など入試で決め打ちで出ることがある。確率や割合の基本ができていれば対応可能。
代表問題例：親がAaとAaのとき、子にaaが生まれる確率は？（1/4 = 25%）
対策：確率の基本（場合の数と比）を押さえる／表（〇×表）で可視化

付録：今日から使える「5分チェックリスト」

テスト前や復習にすぐ使える短いチェックリストを置いておきます。

公式の意味を一文で説明できるか？
与えられた値の単位は揃っているか？
図や条件をすべて確認したか？（見落としはないか）
式は途中式まで書いているか？（答案は途中式で得点）
結果の単位と桁が妥当か？（常識チェック）

中1理科の問題：密度の計算問題

中1理科の範囲で、密度の計算はよく出てきます。「密度」という言葉がちょっとわかりにくいかもしれません。

密度は、「どれだけモノがぎゅっと詰まっているか」です。ざっくり説明すると下記のとおりです。

密度が大きい→ぎゅうぎゅう詰め
密度が小さい→スカスカ

なお、密度の求め方について以下の記事でさらに詳しく解説しています。
中学生必見！理科「密度の求め方」をわかりやすく解説【質量・体積・問題付き】

参考：教育出版 – 理科計算ドリル① 『密度』

密度を求める公式

密度を求める公式は下記のとおりです。

密度（g/cm³）＝物質の質量（g）/物質の体積（cm³）

地理で出てくる「人口密度」と考え方も計算方法も似ています。

密度を求める計算問題

(1)質量が10g、体積が5cm³の物質の密度は何g/cm³になるか。

(2)質量が8.4g、体積が2.8cm³の物質の密度を求めなさい。

(3)質量20gの物質を、20.0cm³の水が入ったメスシリンダーに入れたところ、メモリは25.0cm³になった。この物質の密度を求めなさい。

(4)質量24.8gの物質を、18.0cm³の水が入ったメスシリンダーに入れたところ、メモリは26.0cm³になった。この物質の密度を求めなさい。

(5)下記の表で、密度が一番大きい物質を答えなさい。

	質量	体積
物質A	10g	5.0cm³
物質B	8g	2.0cm³
物質C	50g	25.0cm³

密度の解答と解き方

(1)2g/cm³

10g÷5cm³

(2)3g/cm³

8.4g÷2.8cm³

(3)4g/cm³

体積：25.0cm³-20.0cm³=5.0cm³

密度：20g÷5.0cm³

(4)3.1g/cm³

体積：26.0cm³-18.0cm³=8.0cm³

密度：24.8g÷8.0cm³

(5)物質B

物質Aの密度：10g÷5.0cm³＝2g/cm³

物質Bの密度：8g÷2.0cm³＝4g/cm³

物質Cの密度：50g÷25.0cm³＝2g/cm³

中1理科の問題：水溶液の計算問題（濃度など）

水溶液は中1で出てくる化学範囲で、苦手にする子がたくさんいます。溶質・溶媒・溶液といった日常生活で聞きなれない言葉が出てきます。ややこしく感じる人は

溶媒→水
溶質→水に溶かすもの（砂糖など）
溶液→水に何か溶かした状態のもの（砂糖水など）

と覚えておきましょう。

参考：「ちばのやる気学習ガイド」理科1年生 – 千葉県教育委員会

濃度を求める公式

濃度（%）＝溶液の質量（g）/溶質の質量（g）×100

溶質の質量（g）=溶液の質量（g）×濃度（%）

水溶液の計算問題（濃度など）

(1)80gの水に食塩20gを入れて食塩水をつくった。この食塩水の濃度は何%か。

(2)200gの食塩水25%に食塩は何g溶けているか。

(3)下記の表は水の温度と100gの水に溶ける砂糖の質量との関係である。

水の温度（℃）	20	80
100gの水に溶ける砂糖の質量（g）	200	360

①20℃の水100gにできるだけ砂糖を溶かした。その砂糖水の温度を80℃まで上げるとさらに何gの砂糖を溶かすことができるか。

②80℃の水150gに500gの砂糖を溶かした後20℃まで砂糖水を冷やしたところ、結晶が出てきた。結晶は何gできたか。

③80℃の水200gに600gの砂糖を溶かした後20℃まで砂糖水を冷やし、水を100g加えた。このとき何gの砂糖が溶けのこるか。

解答

(1)20%

食塩20g÷(水80g+食塩20g)×100

(2)50g

食塩水200g×0.25（濃度25%）

(3)
①160g

20℃で溶ける砂糖は200g
80℃で溶ける砂糖は360g

360g-200g=160g

②200g

80℃の水100gで溶ける砂糖は360g
→　80℃の水150gなら溶ける砂糖は1.5倍の540gになるので、砂糖500gはすべて溶ける

20℃の水150gに溶ける砂糖は300g（200g×1.5）なので、

500g-300g=200g

③0g

80℃の水100gで溶ける砂糖は360g
→　80℃の水200gなら溶ける砂糖は2倍の720gになるので、砂糖600gはすべて溶ける

20℃に冷やしてから水100gを足しているので、
水は合計300gになっている
→　20℃の水300gに溶ける砂糖は600g（200g×3）なので、溶けのこりはない。

中1理科の問題：音の速さを求める計算問題

音が伝わるまでの時間や音源までの距離、音の速さを求める問題です。

遠くの打ち上げ花火と自身との距離を求める問題がよく出てきます。

なお、音の速さの計算について、以下の記事でさらに詳しく解説しています。
【中1理科】音の伝わり方をわかりやすく解説！ヘルツの計算問題の解き方とテスト対策

参考：中学生への挑戦状理科 | 京都府教育委員会学校教育課

音の伝わる時間や音源までの距離、音の速さを求める公式

下記の式で時間や距離を求められます。

速さ＝距離÷時間
時間＝距離÷速さ
距離＝速さ×時間

音の速さなどを求める計算問題

(1)音の速さを340m/sとすると、1700m先の花火の音が聞こえてくるまで何秒かかるか。

(2)音の速さを340m/sとする。花火があがってから音が聞こえるまで2秒かかったとすると、花火は何m先で上がったことになるか。

(3)2240m先の花火の音が7秒後に聞こえたとすると、音が空気中を伝わる速さは何m/sか。

(4)自宅にいるとき、花火が上がるのが見えた。花火が開いたのが見えてから音が聞こえるまで4秒かかった。その後祖父母の家に移動して花火を見物した。祖父母の家では花火が開いてから音が聞こえるまで2.5秒かかった。花火までの距離は、自宅と祖父母の家だとどちらのほうが何m近いか。ただし、音の速さは340m/sとする。

解答

(1)5秒

1700m÷340m/s

(2)680m

340m/s×2秒

(3)320m/s

2240m÷7秒

(4)祖父母の家のほうが510m近い

花火の音が聞こえるまでの時間：
自宅は4秒
祖父母宅は2.5秒

→　祖父母宅のほうが1.5秒短い

音の速さは340m/sなので、
340m/s×1.5秒＝510m

中1理科の問題：地震の計算問題

中1理科・地学分野の地震で計算問題がよく出てきます。公式というほどのものはなく、初期微動・主要動・震源が分かれば計算はむずかしくありません。

なお、地震の計算問題の解き方については、以下の記事でさらに詳しく解説しています。
【中学理科】地震の計算問題：震源距離・初期微動の求め方と解き方をわかりやすく解説

参考：中学生への挑戦状理科 | 京都府教育委員会学校教育課

おさらい

地震が発生すると、

まずP波によって初期微動が伝わり、

つづいてS波によって主要動が伝わります。

初期微動が伝わってから主要動が始まるまでの時間を「初期微動継続時間」といいます。

「速さ」の問題と解き方は同じで、地震の伝わる速さ・初期微動継続時間などの時間・震源やある地点までの距離を使って計算します。

速さの公式

速さ＝時間×距離
時間＝距離÷速さ
距離＝距離÷時間

地震のゆれの計算問題

(1)地震が発生し、17時15分20秒にP波が伝わり17時15分28秒にS波が伝わった。このとき、初期微動継続時間は何秒か。

(2)ある地震の記録が下記の表のとおりだったとする。資料の一部が欠けていた。

地点	震源からの距離	初期微動が始まった時刻	主要動が始まった時刻
A	20km	午前10時20分30秒	午前10時20分35秒
B	40km	午前10時20分35秒	午前10時20分秒

①B地点で主要動が始まった時刻は午前10時20分何秒か。

②震源から80kmの地点では、主要動が始まるのは午前何時何分何秒か。

③この地震が発生したのは午前何時何分何秒か。

解答

(1)8秒

初期微動継続時間は「P波が伝わってからS波が伝わるまでの時間」なので、

17時15分28秒-17時15分20秒＝8秒

(2)①午前10時20分45秒

20km地点で初期微動継続時間が5秒とわかる。
40km地点ならその2倍の10秒になる。午前10時20分35秒の10秒後に主要動が始まるので、10時20分45秒。

②午前10時21分5秒

主要動が始まるのは、
20km地点で午前10時20分35秒
40km地点で午前10時20分45秒。
→　20km離れると主要動の開始が10秒遅くなることがわかる。

20km地点から80km地点まで60km離れているので、
3倍（60km÷20km）の30秒遅くなる。

③午前10時20分25秒

①より、P波は20km地点まで5秒で到達していることがわかる。
震源から20km離れたA地点に到達しているのが午前10時20分30秒なので、その5秒前に地震が発生していることになる。

中2理科の問題：化学変化と質量の計算問題（酸化と還元）

化学変化は中2の理科で苦手な子の多い単元です。酸化と還元の実験はパターン化されているのですが、「気体と結びついて質量が大きくなる」という点がイメージしづらいかもしれません。固体や液体同様に気体にも重さがあります。

以下の記事で、中学のテストで出やすい元素記号を紹介しています。
中学生が覚えておくべき元素記号の一覧：覚えやすい語呂合わせと練習問題付き

参考：中学生への挑戦状理科化学変化とイオン – 京都府教育委員会

化学変化と質量の計算問題の解き方

酸化と還元の範囲では、銅と酸素が結びついて酸化銅になるといった変化の仕方を扱います。このとき、銅の質量が12gで酸素の質量が3gとすると、酸化銅はその合計なので15gになります。

解き方はこのとおりシンプルですが、
永遠に「銅＋酸素→酸化銅」のように結びついていく（いくらでも酸化銅の質量が増えていく）わけではありません。一定の量になったら、もう結びつかなくなります（酸化銅の質量は増えなくなります）。
これがあるために表・グラフの読み取りがややこしくなってしまう子が多いです。

表・グラフを読み取って計算する問題を数多くこなせば早く慣れられます。しかも1度慣れれば表・グラフの読み取り問題は非常に解きやすくなります。

化学変化と質量の計算問題

(1) 下記の表は、銅の粉末4.0gを何回か加熱して質量をはかったものです。

	1回目	2回目	3回目	4回目	5回目
加熱後の質量	4.6g	4.8g	5.0g	5.0g	5.0g

①加熱によって質量が一定の値から増えなくなったのは何回目の加熱のときからか。

②1回目の加熱で銅と結びついた酸素は何gか。

③結びついた銅の質量と酸素の質量の比を最も簡単な整数比で表しなさい。

(2)二酸化炭素で満たされた集気びんのなかでマグネシウムリボン9.0gを燃やしたところ、15.0gの白い粉末と、何gかわからない黒い粉末ができた。炭素と酸素の質量を3:8とするとき、以下の問題に答えてください。

①黒い粉末は何gできたか。

②白い粉末を20.0gつくるには何gのマグネシウムリボンが燃やせばいいか。

解答

(1)①3回目

3回目～5回目まで加熱後の質量は5.0gから変わっていない。

②0.6g

4.0gの銅を加熱したら4.6gになっている。増加した分が酸素なので、
4.6g-4.0g=0.6g

③銅：酸素=4：1

4.0gの銅を加熱したところ、5.0gまで質量が増加している。

5.0g-4.0g=1.0gが酸素だとわかる。

(2)①2.25g

マグネシウムリボン9.0gを加熱したら15.0gになっている。増加した質量は酸素なので、酸素6.0gが結びついたとわかる。

また、黒い粉末は6.0gの酸素と結びついた炭素である。

炭素：酸素＝3：8なので、下記のように比例式にして解く。

炭素：6.0g＝3：8
炭素＝18/8
炭素＝2.25g

②12.0g

マグネシウムリボン9.0gに対して酸素6.0gが結びついて15.0gの酸化マグネシウム（白い粉末）ができているので、

マグネシウムリボン：酸化マグネシウム＝9.0：15.0
＝3：5だとわかる。

マグネシウムリボン：酸化マグネシウム20.0g＝3：5

マグネシウムリボン＝12.0g

中2理科の問題：電流の計算問題

中2物理分野の電流は、計算問題が定期テストでよく出題されます。高校入試にも頻出です。

覚えないといけない公式が他分野にくらべて多いので、覚えながら計算練習しましょう。

参考：中学校2年（理科） – 石川県

オームの法則（公式）

電圧をV、電流をI、抵抗をRとすると下記の公式が成り立ちます。

V=R×I
I=V/R
R=V/I

3つとも覚えておくか、どれか1つを覚えておいて残り2つを計算で求めるようにしましょう。

直流回路の電流・電圧・抵抗の求め方

直流回路では下記の3点を覚えておきましょう。

電流：回路のどの点でも等しい
電圧：各区間の電圧の和が電源の電圧に等しい
抵抗：各抵抗の和は全体の抵抗に等しい

交流回路の電流・電圧・抵抗の求め方

複数の回路をつないだ交流回路では下記の3点を覚えておきましょう。

電流：枝分かれした後の電流の和は、枝分かれする前の電流と等しい
電圧：各区間の電圧はすべて電源の電圧に等しい
抵抗：全体の抵抗は各区間の抵抗より小さい

電流・電圧・抵抗の計算問題

(問題)

下記の回路図について後の問題に答えてください。

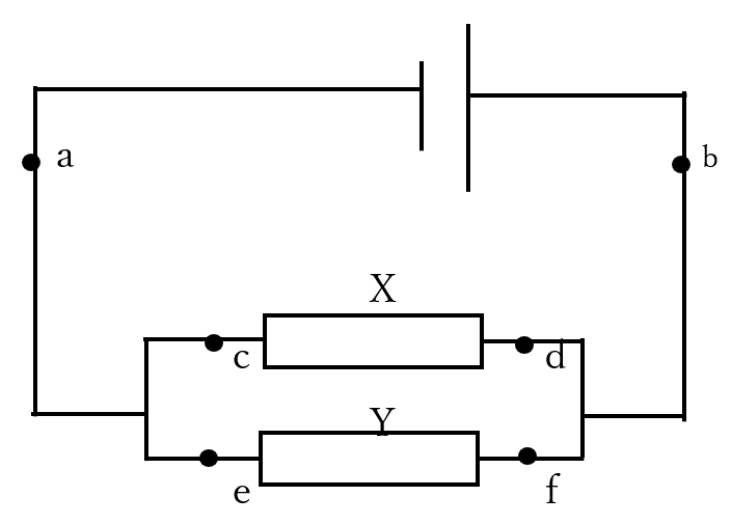
(1)a点を流れる電流が2Aで、d点を流れる電流が1.2Aだった。このとき、b点、c点、e点、f点を流れる電流の大きさを求めてください。

(2)電源の電圧を4Vとしたとき、cd間、ef間の電圧はそれぞれ何Vになりますか。

(3)抵抗器Xと抵抗器Yの抵抗の大きさは何Ωになりますか。

(4)この回路全体の抵抗の大きさは何Ωになりますか。

解答

(1)b点：2A、c点：1.2A、e点：0.8A、f点：0.8A

枝分かれした後の電流の和は、枝分かれする前の電流と等しい。

a点= c点＋e点＝d点＋f点=b点
c点=d点
e点＝f点

(2)cd間：4V、ef間：4V

各区間の電圧はすべて電源の電圧に等しい。

(3)抵抗器X：10/3Ω、抵抗器Y：5Ω

R=V/I（抵抗＝電圧÷電流）

抵抗器X：4V÷1.2A
抵抗器Y：4V÷0.8A

(4)2Ω

回路全体の抵抗＝回路全体の電圧÷回路全体の電流

4V÷2A

中2理科の問題：圧力の計算問題

中2の気象の範囲で圧力の計算問題が出てきます。

圧力は、「どれだけの力が加わっているか」を表しています。

参考：山口県教育委員会 – やまぐちっ子学習プリント >> 中学校 1年生理科

圧力を求める公式

圧力は以下の公式で求められます。

圧力（Pa）＝面を垂直に押す力（N）÷力が働く面積（m²）
1N＝質量100gの物体にかかる重力

1m²あたりに何N（ニュートン）働いているかを求めます。

圧力を求める計算問題

(1)質量200gで1辺20cmの立方体がある。

①この立方体に働く重力はいくらか。

②面を下にしてスポンジに置いたとき、スポンジが受ける圧力はいくらか。

(2)下記の表のような物体Aと物体Bがある。

	物体A	物体B
質量（g）	200	500
底面積（m²）	40	200

①力の大きさはどちらの物体のほうが大きいか。

②圧力はどちらの物体のほうが大きいか。

③物体Aを2つ積み上げた時の圧力はいくらになるか。

解答

(1)①2N

質量100gで1N

②50Pa

圧力（Pa）＝面を垂直に押す力（N）÷力が働く面積（m²）

①より、「面を垂直に押す力」は2N
「力が働く面積（m²）」は0.2m×0.2m=0.04m²

→　2N÷0.04m²=50Pa

(2)①物体B

質量の大きいほうが力の大きさも大きい

②物体A

物体Aの圧力：200g÷40m²=5Pa
物体Bの圧力：500g÷200m²=2.5Pa

(3)10Pa

物体A1つで5Paの圧力がある。2つなら5Pa+5Pa=10Pa。

中2理科の問題：水蒸気の計算問題（湿度、飽和水蒸気量など）

気象の範囲で、湿度を求める計算問題も非常によく出てきます。

参考：山口県教育委員会 – やまぐちっ子学習プリント >> 中学校 2年生理科

湿度を求める公式

湿度は下記の公式で求められます。

湿度(%)=空気1m³中に含まれる水蒸気量（g/m³）÷その空気と同じ気温での飽和水蒸気量（g/m³）×100

長ったらしくなりますが、
「空気中に100まで水分を貯められるとして、今どれくらいの水分が空気中にあるのか」を表す数字が湿度です。

水蒸気の計算問題

（問題）下記の表を用いて問題に答えてください。

気温（℃）	飽和水蒸気量（g/m³）
5	7
10	8
15	9.5
20	11.5
25	14

(1)現在の気温が20℃で1m³中の水蒸気量が8g/m³のとき、1m³中にあと何gの水蒸気を含むことができますか。

(2)現在の気温が10℃で1m³中の水蒸気量が6g/m³のとき、湿度は何%ですか。

(3)現在の気温が25℃で1m³中の水蒸気量が9.5g/m³のときの露点は何℃ですか。

(4)現在の気温が25℃で湿度が70%のとき、気温が5度に下がると空気1m³あたり何gの水滴が出てくるか。

解答

(1)3.5g/m³

1m³中の水蒸気量が8g/m³で、20℃のときの飽和水蒸気量が11.5g/m³。

(2)75%

10℃のときの飽和水蒸気量が8g/m³で、現在6g/m³。

6÷8×100=75%

(3)15℃

飽和水蒸気量が9.5g/m³になったときが露点（水滴が出てくる温度）

(4)2.8g/m³

空気1m³あたりの現在の水蒸気量は
14×0.7=9.8g/m³

気温が5℃のときの飽和水蒸気量が7g/m³なので、
9.8-7=2.8g/m³

中3理科の問題：運動の速さの計算問題

中3で運動が出てきます。記録タイマーで打点された用紙をみて解く問題が多く、算数の速さと同じ解き方をします。

参考：「ちばのやる気学習ガイド」理科3年生 – 千葉県教育委員会

運動：速さの求め方

運動の公式は下記のとおりです。「台車の動く平均の速さ」や「球による自由落下の平均の速さ」を求める問題が多いです。

速さ＝移動した距離÷移動するのにかかった時間

運動：台車の計算問題

(1)1秒間に50回打点する記録タイマーがあるとする。このタイマーは何秒に1回ずつ打点しているか。

(2)1/60秒ごとに打点する記録タイマーが20回打点するのにかかる時間は何秒か。

(3)斜面を下る台車の運動を、1秒間に50回打点する記録タイマーを使って記録した。
A点からB点まで4.5cm、A点からC点まで12cmのとき、以下の問いに答えてください。

①A点が打点されてからC点が打点されるまでの時間は何秒か。

②A点が打点されてからB点が打点されるまでの平均の速さは何cm/sか。

③B点が打点されてからC点が打点されるまでの平均の速さは何cm/sか。

④A点が打点されてからC点が打点されるまでの平均の速さは何cm/sか。

解答

(1)1/50秒

50回打点するのに1秒なので、1÷50

(2)1/3秒

1/60秒で1回打点するので20回打点するには、
1/60×20

(3)①1/5秒

1秒間に50回打点するので、1回打点するのに1/50秒。
A点からC点まで10回打点しているので、
1/50×10

②45cm/s

A点からB点までの距離は4.5cmで時間は5/50秒＝1/10秒。
4.5cm÷1/10秒

③75cm/s

B点からC点までの距離は12cm-4.5cm=7.5cmで、
時間は5/50秒＝1/10秒。
7.5cm÷1/10秒

④60cm/s

A点からC点までの距離は12cmで時間は1/5秒。
12cm÷1/5秒

（別解）
A点からB点までが45cm/sで
B点からC点までが75cm/s。

(45+75)÷2=60cm/s。

運動：自由落下の計算問題

(問題)球が自由落下する様子を0.1秒ごとに発行するストロボスコープで記録した。

A点からB点までは5.0cm、B点からC点までは8.0cm、C点からD点までは14.0cmだった。

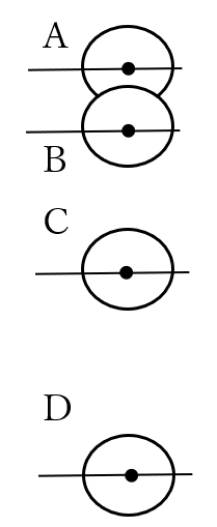
(1)球が落下しはじめてから0.2秒間の落下距離は何cmか。

(2)球が落下しはじめてから0.1秒後から0.3秒後までの落下距離は何cmか。

(3)球が落下しはじめてから0.3秒間の平均の速さは何cm/sか。

解答

(1)13.0cm

落下しはじめてから0.2秒間でC点まで移動していることになる。
A点→B点が5.0cm
B点→C点が8.0cm
→　A点→C点は13.0cm

(2)22.0cm

落下しはじめてから0.1秒後はB点で、
落下しはじめてから0.3秒後はD点。

(3)90cm/s

落下しはじめてから0.3秒間で27.0cm（A点からC点までの距離）移動している。

27÷0.3=90

中3理科の問題：仕事の計算

中3理科では物体の運動につづいて「仕事」が登場します。物体を押してその方向に動かしたら「仕事をした」ということになります。

物体を動かすとき、同じ力でも動かし方（持ち上げるのが、斜面に沿って引き上げるのかなど）によって物体の移動距離は変わります。それを仕事率（仕事の能率）と言います。

参考：教育出版：理科計算ドリル⑩ 『仕事と仕事率』

仕事の大きさを求める公式

仕事の大きさを求めるには以下の計算をします。

仕事（J）＝力の大きさ（N）×力の向きに移動した距離（m）

仕事率を求める公式

仕事率は以下の式で求められます。

仕事率（W）＝仕事（J）÷かかった時間（s）

仕事の計算問題

(1)水平な床の上に400gの木片を置き、手を使って一定の速さで50cm動かした。動かしている間の力の大きさをはかったところ、ばねばかりの目盛りは3Nだった。

①動いている木片にはたらく摩擦力の大きさは何Nか。

②木片を動かす手の仕事の大きさは何Nか。

(2)てこの一方に4kgの物体を置き、手を使って10秒かけて反対側を80cm押し下げて物体を50cm持ち上げた。100gの物体にはたらく重力の大きさを1Nとして、以下の問題に答えてください。

①てこの反対側を手で押し下げたときに行った仕事は何Jか。

②てこの反対側を手で押し下げたときに行った力は何Nか。

③てこの反対側を手で押し下げたときに行ったときの仕事率は何Wか。

解答

(1)①3N

水平な面で物体を動かすときは、物体を動かす力と摩擦力は同じ

②1.5J

3N×0.5m

(2)①32J

100gの物体にはたらく力が1Nとしている。物体は4kgで80cm動いているので、

40N×0.8m

②40N

仕事（J）＝力の大きさ（N）×力の向きに移動した距離（m）にxや数字を入れる。

32J=x×0.8m
x=32÷0.8

③3.2W

仕事率（W）＝仕事（J）÷かかった時間（s）の式を使う。

W=32J÷10秒

中3理科の問題：エネルギーの計算問題

運動エネルギーを熱エネルギーに変換するときなどの変換効率を求める問題が中3理科で出てきます。

参考：「ちばのやる気学習ガイド」理科3年生（運動とエネルギー） – 千葉県教育委員会

変換効率を求める公式

変換効率（%）＝目的のエネルギー（J）÷もとのエネルギー（J）×100

エネルギーの計算問題

(問題)

モーターに電流を流して10秒かけて300gのおもりを2m引き上げる実験を行った。モーターを電流計、電圧計につないだところ、電流計は2.0A、電圧計は1.0Vを示していた。100gの物体にはたらく重力の大きさを1Nとする。

①消費した電力量の大きさは何Jか。

②仕事量の大きさは何Jか。

③この実験でのエネルギー変換効率は何%か。

解答

①20.0J

消費した電力の大きさは
2.0V×1.0A=2.0W

10秒間で消費した電力量の大きさは、
2.0W×10s=20.0J

②4.0J

100gの物体にはたらく重力が1Nなので、200gの物体なら2N。2m動かしているので、
2N×2m=4.0J

③20%

変換効率（%）＝目的のエネルギー（J）÷もとのエネルギー（J）×100で求められる。

「目的のエネルギー」は物体を引き上げる力で4.0J、
「もとのエネルギー」は10秒間で消費した電力量の大きさで20.0J

4.0÷20.0×100=20%

分野横断で使える！中学理科の計算公式一覧表

中学理科では、分野ごとに異なる計算公式を使いますが、実はどの分野でも「比・比例・単位変換」の考え方は共通しています。

この章では、物理・化学・地学・生物の重要公式と、テスト・入試で役立つ単位変換表、そして練習用プリントの使い方を紹介します。

※参考：東京書籍『新しい科学』

物理・化学・地学・生物の重要公式まとめ

中学生が必ず覚えておきたい計算公式を、分野別に整理しました。
「公式だけ」でなく「意味」や「使うときの注意」もあわせて理解することが、得点アップのカギです。

物理分野の公式

分野	公式	意味・使い方のポイント
速さ	速さ＝距離÷時間	単位をm/sやkm/hにそろえる。時間は秒に直すこと。
密度	密度＝質量÷体積	体積の単位をcm³やm³に注意。小数の扱いに慣れる。
圧力	圧力＝力÷面積	力はN（ニュートン）、面積はm²で計算する。
仕事	仕事＝力×距離	単位はJ（ジュール）。力と距離は同じ向きの場合のみ計算できる。
電流・電圧	電圧＝電流×抵抗（オームの法則）	V＝IR。単位はV, A, Ω。回路図の見方をセットで理解。

化学分野の公式

分野	公式	意味・使い方のポイント
濃度	濃度（％）＝（溶質の質量÷溶液の質量）×100	「溶液の質量＝溶質＋溶媒」であることに注意。
質量保存	反応前の質量＝反応後の質量	反応式に合わせて係数比で考える。
気体の発生量	反応の比から気体の体積を求める	反応式の係数を比に使う。

地学分野の公式

分野	公式	意味・使い方のポイント
地震	震源距離＝P波・S波の到達時間差×（速さの差）	グラフの読み取り練習が重要。
湿度	湿度（％）＝（実際の水蒸気量÷飽和水蒸気量）×100	単位をg/m³にそろえる。グラフ問題が出やすい。

生物分野の公式

分野	公式	意味・使い方のポイント
光合成・呼吸	吸収・放出する気体の量で計算	酸素と二酸化炭素の量を図で整理。
遺伝	子の組み合わせの確率＝（それぞれの親の確率の積）	表（AA, Aa, aaなど）を書いて整理。
個体数変化	変化率＝（増減量÷もとの数）×100	増減の方向（＋／−）に注意。

単位変換の早見表（cm³↔m³、g↔kg など）

理科の計算で最も多いミスの一つが「単位ミス」です。
以下の表を参考に、テスト前に10秒で確認できるよう暗記しておくと安心です。

種類	小さい単位 → 大きい単位	変換方法	例
長さ	cm → m	÷100	100 cm = 1 m
面積	cm² → m²	÷10,000	10,000 cm² = 1 m²
体積	cm³ → m³	÷1,000,000	1,000,000 cm³ = 1 m³
質量	g → kg	÷1,000	1,000 g = 1 kg
時間	分 → 秒	×60	1 分 = 60 秒
体積（液体）	mL → L	÷1,000	1,000 mL = 1 L
力	1 N	100gの物体にかかる重力	覚えておくと物理で便利

【単位変換のコツ】

「大きくなると数字が小さくなる、小さくなると数字が大きくなる」
計算前に「全部の数値の単位をそろえる」
テスト直前は上表を3回声に出して読むと定着が早いです。

テスト・入試対策の実践ステップ

ここでは、公式の暗記から入試対応までの3ステップ学習法を紹介します。
計算問題は「理解 → 練習 → 応用」の順で学ぶことで、安定した得点につながります。

ステップ①：よく出る公式を覚える

目的： 基本の土台を作る。
内容： まずは「頻出公式」を頭に入れ、意味を理解する段階。

【具体的なやり方】

教科書・ノートから「公式」を一覧化して自分専用の“公式カード”を作る。
1日3分、朝や寝る前に声に出して読む（暗唱法）。
「この公式はどんな現象を表しているか？」を一言で説明できるようにする。

【ポイント】

覚えにくい公式は図とセットで記憶。
「物理→化学→地学→生物」の順で覚えると理解しやすい。

ステップ②：例題で理解を深める

目的： 暗記した公式を「使える」ようにする。
内容： 実際の問題を解きながら、計算の流れをつかむ。

【学習の流れ】

例題を1問解く（途中式を丁寧に書く）
自分のミスを確認する（単位・読み間違いなど）
正しい解法をノートにまとめて再解答
類題を3問ほど解いて定着させる

【ポイント】

計算式の前に、使う公式と求める量を必ず書く。
「なぜその公式を使うのか」を説明できるようにする。
苦手な分野は1日1問ずつでもOK、継続が最重要。

ステップ③：応用問題で得点力アップ

目的： 入試レベルの複合問題に対応する。
内容： 文章が長く、複数の公式や条件を組み合わせる問題に挑戦。

【効果的な練習法】

グラフ・表の読み取りを含む問題を中心に解く。
問題を解く前に「使う公式のリストアップ」から始める。
間違えた問題は「どの段階で間違えたか」をノートに書く。

【アドバイス】

模試や過去問を時間を計って解く（制限時間15〜20分）。
間違えノートを作り、「原因別に分類」（単位ミス・公式選択ミス・読み間違え）すると弱点克服が早い。

【入試対策】都道府県別の出題傾向まとめ

入試では、地域ごとに出題傾向に特徴があります。
以下は代表的な都道府県別の傾向と対策例です。

地域	傾向	対策ポイント
東京・神奈川	文章量が多く、グラフ・表を使った総合問題	読解力＋複数公式の使い分け練習
大阪・京都	基礎公式＋実験問題（手順・結果の解釈）	実験の意図を理解、図示問題を練習
愛知・岐阜	計算問題の比率が高く、密度・圧力・濃度の定番	公式暗記＋単位変換を確実に
福岡・広島	化学反応と電気の融合問題が多い	反応式とオームの法則の両方に慣れる
北海道・東北	気象・天体・地震など地学問題が多い	グラフ読解＋P波・S波の計算練習