高校入試の数学でよく出る問題を単元別にまとめました。
学校の実力テスト対策や業者模試対策、高校入試対策にご活用ください。
※関連記事:高校入試の数学でよく出る文章問題
※Z会について下記記事でくわしく紹介しています。
【中学生向け】Z会タブレットコースの進め方:成績上位を取って難関校に合格する方法を解説
高校入試でよく出る数学の問題例と解き方の解説
高校受験で頻出の数学の問題を単元ごとにまとめました。気になる単元の問題を解いてみて下さい。
高校入試数学でよく出る計算問題例
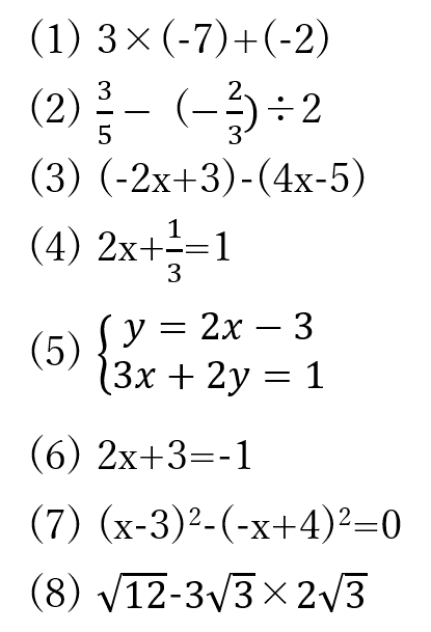
解答
(1)-23
3×(-7)+(-2)
=-21-2
-23
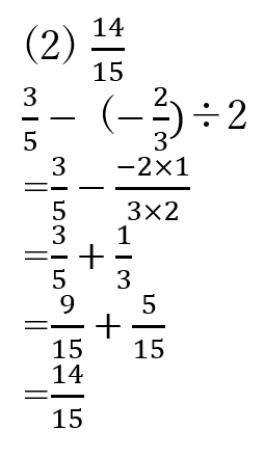
(3) -6x+8
(-2x+3)-(4x-5)
=-2x+3-4x+5
=-6x+8
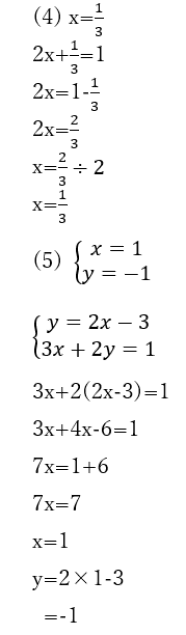
(6) x=-2
2x+3=-1
2x=-4
x=-2
(7) x=2/7
(x-3)2-(-x+4)2=0
x2-6x+9-x2+8x-16=0
2x-7=0
2x=7
x=2/7
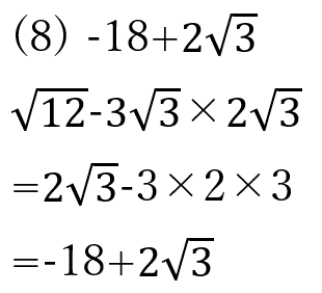
高校入試数学でよく出る比例・反比例の問題例
(1) yはxに比例し、x=6のときy=18である。yをxの式で表しなさい。
(2) 反比例y=のグラフが点(2, -3)を通るとき、aの値を求めなさい。
(3) 関数y=のグラフ上の点で、x座標とy座標がともに整数となる点は全部で何個あるか。
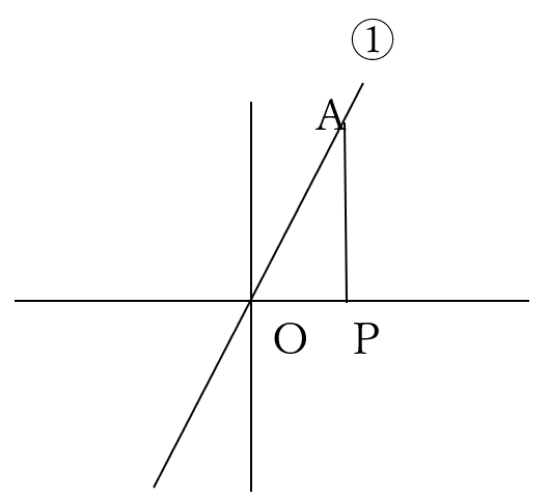
(4) ①は関数y=4xのグラフである。グラフ上にある点Aからx軸に引いた垂線とx軸との交点をPとする。三角形OAPの面積が32になるとき、点Aの座標を求めなさい。
(5) 毎分5Lの割合で水を入れると20分で満杯になる空の水そうがある。
①この水そうに毎分xLの割合で水を入れたときに満杯になるまでの時間をy分として、yをxの式で表しなさい。
②毎分4Lの割合で水を入れると満杯になるまで何分かかりますか。
解答
(1) y=3x
y=axの式に
x=6、y=18を代入する。
18=6a
a=3
(2) y=-6/x
y=の式にx=2、y=-3を代入する。
-3=
a=-3×2
a=-6
(3) 6個
y=の式で、xとyに整数を入れて「=」が成り立つような組み合わせを考える。
xy=12になればいいので、
(x, y)=(1,12) (2,6) (3,4) (4,3) (6,2) (12,1)の6通り
(4) (4, 16)
三角形の面積を求める公式は、
「たて×横÷2」。
このグラフでは、
「たて」=AP
「横」=OPになるので、
AP×OP÷2=32
y=4xということは、xが1増えるたびにyは4増える。たては横の4倍の長さになる。
x×y÷2=32
x×4x÷2=32
2x2=32
x=4
y=16
(5)
① y=100/x
y=の式にx=5、y=20を代入する。
20=
a=100
② 25分
y=100/xにx=4を代入する。
y=100/4
y=25
高校入試数学でよく出る1次関数・2次関数の問題例
(1) yはxの1次関数であり、x=4のときy=10、x=-2のときy=-2になる。yをxの式で表しなさい。
(2) x軸に平行で、点(4, 2)を通る直線の式を求めなさい。
(3) y=ax2において、xの値が3から5に増加するときの変化の割合は4である。このとき、aの値を求めなさい。
(4) 傾きが一定の斜面でボールを転がした。ボールが転がりはじめてからx秒間にボールの進んだ距離をymとすると、yはxの2乗に比例した。ボールが転がりはじめてから3秒間に進んだ距離が18mのとき、yをxの式で表しなさい。
(5)
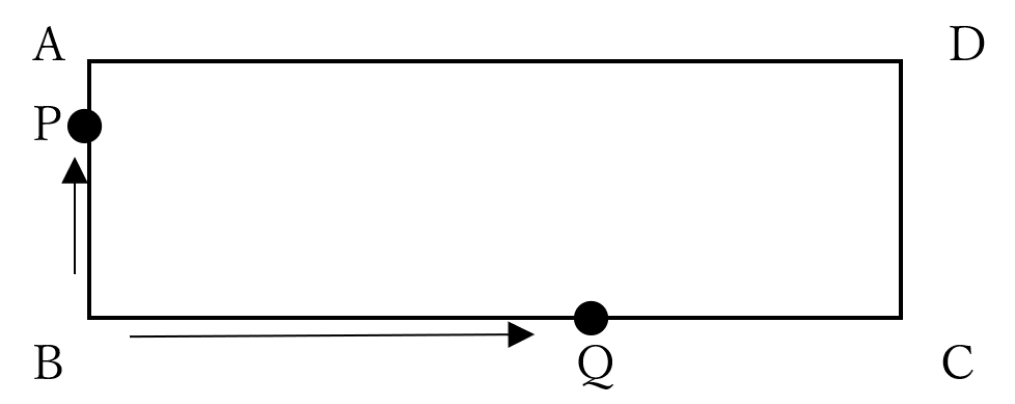
下の図のように、AB=5cm、BC=12cmの長方形がある。点Pは点Bを出発して毎秒1cm進み、点Qは同じく点Bを出発して毎秒2cm進む。点P、Qが点Bを同時に出発してから5秒後の三角形BPQの面積を求めなさい。
解答
(1) a=2、b=2
y=ax+bの式に、x=4、y=10と、x=-2、y=-2を代入する。
10=4a+b
-2=-2a+b
この式を解いて、a=2、b=2
(2) y=2
x軸に平行ということは、x座標に関係なくy座標はずっと同じ。
(3) a=1/2
変化の割合=(yの増加量)÷(xの増加量)なので、
4=(25a-9a)/(5-3)
a=1/2
(4) y=2x2
まず、y=ax2の式をつくる。
3秒間に18m進んだので、
x=3、y=18を代入する。
18=9a
a=2
(5) 25cm2
まず、出発してから5秒後に点P、Qがそれぞれどの位置にあるか考える。
点Pは5秒間で5cm進み、点Qは10cm進んでいるので、
△PBQはBP=5cm、BQ=10cmの直角三角形になっていることがわかる。
5×10×1/2=25cm2
※関連記事:一次関数の利用の解き方と練習問題
高校入試数学でよく出る確率の問題例
(1) 2つのサイコロを同時に投げて、出る目の和が9以上になる確率を求めなさい。
(2) 2つのサイコロを同時に投げて、出る目の数の積が奇数になる確率を求めなさい。
(3) ある箱のなかに、当たりくじ2本と外れくじが1本ある。AさんとBさんが箱の中にあるくじを1本ずつ引くとする。Aさんがくじを引いた後、そのくじを箱に戻さずにBさんがくじを引くとき、AさんとBさんの両方が当たりくじを引く確率を求めなさい。
(4) 10円玉、50円玉、100円玉の合計3枚の硬貨が財布に入っている。その中から同時に2枚を取り出したとき、硬貨の金額の合計が100円以上になる確率を求めなさい。
(5) 48枚のトランプが裏返しに置かれている。その中から同時に3枚を選んだとき、選んだトランプのカードのマークが少なくとも1枚が赤色である確率を求めなさい。ただし、ジョーカーは入っていないとする。
解答
(1)
2つのサイコロを同時に投げたときの出る目の組み合わせは、全部で36通りある。
そのなかで出る目の和(=足し算の答え)が9、10、11、12になるのは下記の10通り。
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ||||||
| 2 | ||||||
| 3 | 〇 | |||||
| 4 | 〇 | 〇 | ||||
| 5 | 〇 | 〇 | 〇 | |||
| 6 | 〇 | 〇 | 〇 | 〇 |
(2)
2つのサイコロを同時に投げたときの出る目の組み合わせは、全部で36通りある。
そのなかで出る目の積(=かけ算の答え)が奇数になるのは下記の9通り。
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 〇 | 〇 | 〇 | |||
| 2 | ||||||
| 3 | 〇 | 〇 | 〇 | |||
| 4 | ||||||
| 5 | 〇 | 〇 | 〇 | |||
| 6 |
(3) 2/3
当たりくじをA、外れくじをaとして樹形図を描く。
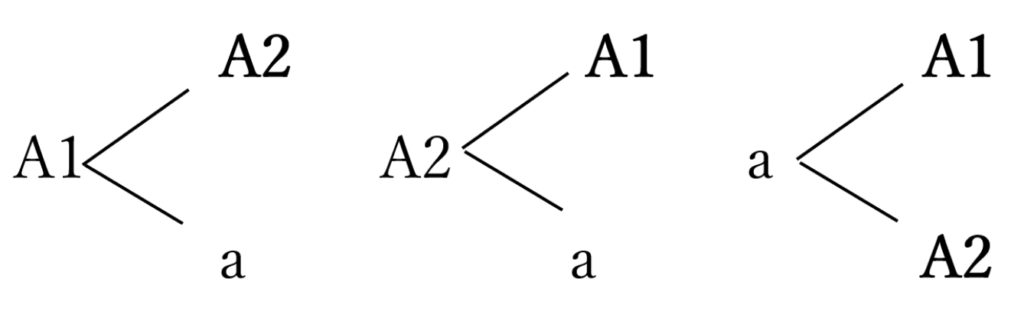
上記の樹形図のように、くじの引き方は全部で6通り。
そのうち、2人とも当たりくじを引くのは4通り。
(4)2/3
3枚の硬貨から2枚を取り出すときの組み合わせは下記の3通り。
a)10円+50円=60円
b)10円+100円=110円
c)50円+100円=150円
「100円以上になる組み合わせ」はb)とc)の2通り。
(5) 7/8
「少なくとも1枚が赤色」のように「少なくとも~」という条件がついている問題では、その逆のケースを考えると良い。この問題では「少なくとも1枚が赤色」なので、その逆は「すべて黒色」の場合を考える。
赤色を〇、黒色を×として樹形図を描いて数える。
すると、「すべて黒色」になる確率が1/8だとわかる。
最後に、「すべて黒色」にならない=「少なくとも1枚が赤色」の確率を求める。
1-1/8=
7/8
確率の裏ワザを以下の記事で解説しています。
【中学数学】確率の裏ワザ:定期テスト・高校入試で高得点を取るコツとおすすめの問題集を紹介
高校入試数学でよく出る図形の問題例
(1)以下の図形の∠ABEの角度を求めなさい。ただし、五角形ABCDEは正五角形とする。

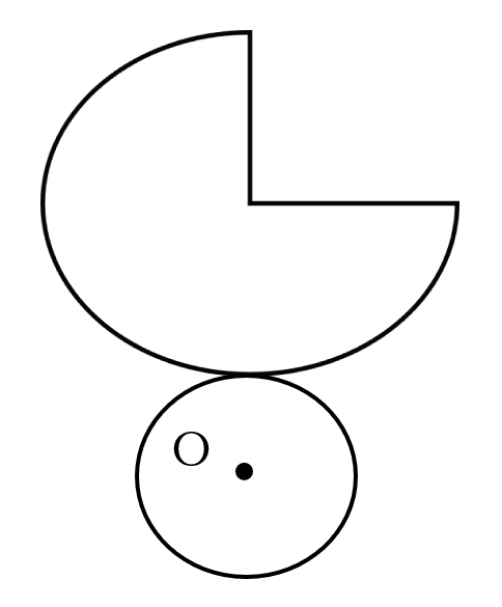
(2)下記の図は中心角270度のおうぎ形である。底面の円Oの半径を求めなさい。
なお、おうぎ形の半径は12cmとする。
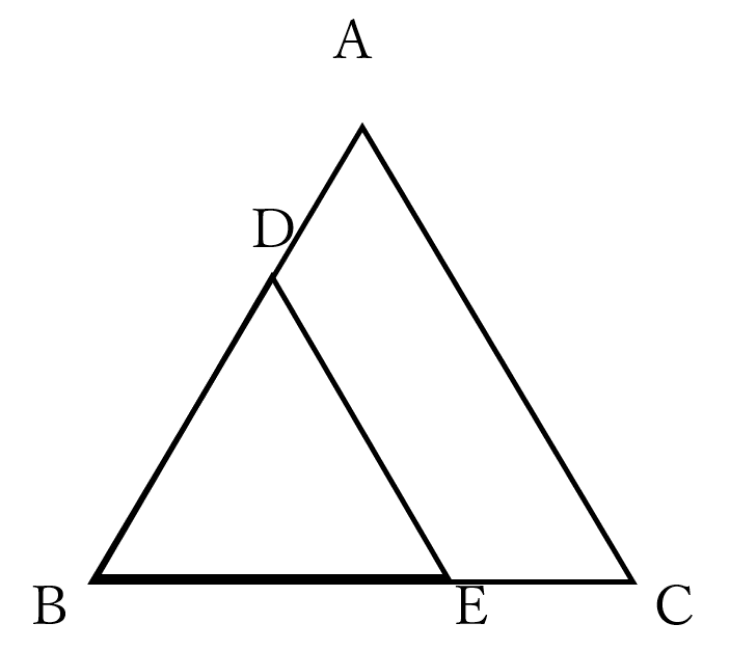
(3)下記の図はAC∥DEの三角形である。AC=8cm、DE=6cm、BC=12cmのとき、BEの長さを求めなさい。
(4)2つの円A、Bがあり、相似比は2:5である。円Aの面積が26πcm2のとき、円Bの面積はいくらになるか。
解答
(1)36°
ABCDEは正五角形なので、辺AB=辺AE。
∠BAEは540°÷5=108°になるので、
∠ABE=(180°-108°)÷2=36°
(2)9cm
おうぎ形の弧の長さ=円Oの円周なので、まずおうぎ形の弧の長さを求める。
12×2×π÷2=18πcm
つづいて、円Oの半径をxcmとして、円Oの円周を求める式をつくる。
x×2×π=18π
x=9cm
(3) 9cm
AC∥DEなので、
BC:BE=AC:DE
12:BE=8:6
BE=9
(4) 325π/2cm2
面積比は相似比の2乗になる。
円A:円B=2:5
26π:円B=22:52
26π:円B=4:25
円B=325π/2
高校入試数学で覚えておきたい計算の公式
乗法公式
(x+a)(x+b)=x2+(a+b)x+ab
(a+b)(a−b)=a2−b2
(a+b)2=a2+2ab+b2
(a−b)2=a2−2ab+b2
解の公式
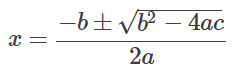
高校入試数学で覚えておきたい関数の公式
高校入試数学で覚えておきたい比例・反比例の公式
比例
y=ax
反比例
y=a/x
一次関数
y=ax+b
二次関数
y=ax2
変化の割合を求める公式
変化の割合=yの増加量/xの増加量
なお、変化の割合や切片の求め方について、以下の記事でくわしく解説しています。
一次関数の変化の割合とは(中学生):変化の割合の求め方を解説(変化の割合を求める練習問題つき)
一次関数の傾きと切片:傾きや切片の求め方と一次関数の式の求め方を解説(練習問題つき)
高校入試数学で覚えておきたい図形の公式
円の面積を求める公式
πr2
周の長さを求める公式
2πr
おうぎ形の面積を求める公式
πr2×(中心角)/360
おうぎ形の弧の長さを求める公式
2πr×(中心角)/360
柱体の体積を求める公式
(体積)=(底面積)×(高さ)
錐体の体積を求める公式
(体積)=(底面積)×(高さ)×1/3
円錐の中心角を求める公式
(半径)/(母線)×360
円錐の側面積を求める公式
(母線)×(半径)×π
三角形の合同や相似で覚えておきたい条件
三角形の合同条件3つ
直角三角形の合同条件2つ
二等辺三角形になる条件2つ
平行四辺形になる条件5つ
三角形の相似条件3つ
相似比・面積比・体積比
【相似比】m:n
【面積比】m2:n2
【体積比】m3:n3
円周角の定理4つ
三平方の定理
斜辺の2乗は他の辺の2乗の和に等しい
(c2=a2+b2)
高校入試数学の勉強方法
高校入試は定期テストより範囲が広く、勉強時間がいくらあっても足りません。ですが中3は内申点の比重が多くの県で高く、受験勉強にそれほど長い時間を回しづらいです。
そこで、数学の入試対策を効率よく進められるようにできる勉強方法をお伝えします。単元ごとにまとめていますので、気になる単元をピックアップしてご活用ください。
計算ミスを減らせる勉強方法
高校入試の計算問題は決して難問ではありません。1問も取りこぼさずに正解を取り切りたいですね。
計算問題での間違え方は2つあります。
- 計算方法がわからない
- わかっていたのにミスをする
計算問題で間違いがなかなか減らない人は、「間違う原因」をまず探りましょう。意外と「計算方法がわかっていなかった(誤解していた)」という人が多いです。
分配法則の仕方、分数の計算の仕方、平方根の計算ルールなど、問題を解きながら自分で解説してみましょう。解説してみれば、計算ルールが定着しているかどうかを自分で確認できます。
計算ルールが分かっているのに間違う場合は、「解き方」が定着していないのかもしれません。定着しきっていない場合、いつもと違う場所で問題を解く、いつもと違う形式の問題を解く、いつもより急いで解いたなどの「いつもとちょっと違う状況」にいるだけでミスが起こりやすいです。
また、最近習ったばかりの問題も1週間経つと忘れてきています。九九の問題も、中学生になればスラスラ解けますしミスもしません。ですが小学生の習いたてのころは幾度となく間違えたはずです。
かけ算やわり算の九九の暗唱を何百回もして脳が「正解のアウトプット」に慣れてくれたから、今ではミスなく九九を使えるようになっているのです。
さすがに高校入試対策で単元ごとに何百回も解くのは時間的にむずかしいですが、正解した問題を翌日もう1度解いてみてください。正解した問題ですから、正しい解き方がわかっているはずです。
問題を解くのに時間がかかりませんし、問題に間違ってしまって「脳に間違ったアウトプットを学習させてしまう」リスクも小さくできます。
比例・反比例、関数の勉強方法
比例・反比例、関数は中1~中3の2学期に学習します。いずれも「一方の数字の変化に合わせてもう一方の数字も変化する」という点で同じです。xが2倍、3倍に増加したらyも2倍、3倍に増加するなど。
文章題やグラフが出てきたら、ひとまずy=axやy=ax2などの式を作るようにしましょう。
あとは、xとyの組み合わせ(x=1のとき、yがいくらになるかなど)を見つければ完成です。
※関連記事:【中学数学】関数、比例・反比例の問題の解き方
xとyの組み合わせを見つけるのに連立方程式や2次方程式を使います。「関数が苦手です」という人のなかには、式をつくるところまでは大丈夫なのにその先の計算方法があやふやになっている人もいます。
そういう人はまず計算の練習をしておきましょう。
確率の勉強方法
確率が苦手な人は、問題ごとに解き方を考えている傾向があります。
確率は問題がパターン化されています。パターンごとに演習をして、解き方に慣れるほうが早いです。
- サイコロを振るパターン
- コインを投げるパターン
- 玉を取り出すパターン
- トランプを引くパターン
それぞれのパターンでの解き方を覚えておけば、迷うことなく正しく解けます。
※関連記事:【中学数学】確率の求め方の裏ワザ
また、樹形図を描くときは下記のように「数字や記号の若い順」に書きましょう。
1→2→3
a→b→c
これだけで書きもれを防げます。
図形の勉強方法
図形はまず「公式や条件・性質」を覚えましょう。合同条件や相似条件はもちろん、「多角形の角の性質」「平行四辺形の性質」などの細かいところまで覚えておきましょう。
図形の問題は「どの条件・性質を使うか」の選択で決まります。どの条件・性質を使うかが問題を見てすぐにわかる問題もありますが、入試では「すぐにわからない問題」のほうがよく出ます。
図形に長さや角の大きさを書き入れたり、平行な線分はないか、「二等辺三角形」「正方形」のように辺の長さや角の大きさが等しいことが織り込み済の図形はないかなどを探します。
そこから「使えそうな条件・性質」の候補をしぼりこんでいきます。
また、過去問対策が非常に有効な単元でもあるので、過去問を10年分は解くようにしましょう。
※関連記事:【中学数学】平面図形・空間図形の解き方とコツ
高校入試によく出る応用問題をパターン別に演習する
高校入試の数学の問題はある程度パターンが決まっています。パターンごとに何度か問題を解くと、解き方を定着させられます。
上記は入試で最頻出の問題です。学校のワークや市販の問題集などを使って繰り返し解いてみましょう。
※関連記事:3つの連続する整数の解き方
※関連記事:2ケタの整数の10の位の数と1の位の数を入れ替える文章問題などの解き方
※関連記事:ある数xの2倍が10からxの3倍を引いた数と等しいときのxの求め方
通信教育を活用する
社会は暗記科目です。暗記するには、繰り返しの学習と視覚記憶が有効です。
通信教育なら何度でも学習できますし、視覚的に理解しやすい(印象に残りやすい)解説動画を視聴できます。
しかも大手の通信教育なら問題の正解・不正解に応じて「解くべき問題」を提示してくれる機能があります。復習も最適なタイミングで実施できます。
月2,178円で受け放題のスタディサプリ
スタディサプリは視覚的に理解しやすい授業を特徴としています。何度も受講できるので、説明動画を頭に焼き付けることができます。
また、高品質な授業動画に加えて10万問以上の演習問題があり、月10,780円で個別指導も受けられます。
くわしくは、スタディサプリ中学講座の特徴と効果的な活用法で紹介しています。
受講者数No. 1の進研ゼミ
やはり通信教育といえば進研ゼミです。受講者数No. 1で、昔から高校受験対策に定評があります。
高校入試情報をタイミングよく配信してくれますし、苦手克服から難関校対策まで幅広いレベルに対応しています。解説動画を学校の予習代わりに使って1日15~30分の勉強で高得点をねらうことも可能です。
くわしくは、進研ゼミ中学講座の特徴と効果的な利用法で紹介しています。
高校入試数学対策の参考書・問題集
総合問題集・入試頻出問題集を3種類紹介します。
『2025年受験用 全国高校入試問題正解 数学』

2025年受験用 全国高校入試問題正解 数学
分野別に勉強できるものもあります↓

2025年受験用 全国高校入試問題正解 分野別過去問 449題 数学 図形
出版社:旺文社
特徴:
2024年高校入試より数学の問題と解答解説を掲載。47都道府県の公立高校と主な国立・私立および高等専門学校を収録。都道府県別・高校ごとに「出題傾向と対策」、問題ごとにくわしい「解き方」を解説。最新の高校入試問題を系統別に分析・学習できる入試対策必須の一冊。思考力を問う問題には、思考力マークを表記。
Amazonより引用
【おすすめする理由】
総合問題演習をしたい人全般におすすめです。
全国の高校入試問題を掲載しており、とにかく大量に演習できます。
小問集合ばかり解いてみるなど、使い方は自由です。
『高校入試 合格でる順 数学 五訂版』

高校入試 合格でる順 数学 五訂版
出版社:旺文社
特徴:
●高校入試の問題を分析し,出題率の高い順に単元を並べた問題集です。出題率の高い順に学習をすることで,効率的に合格に近づくことができます。
旺文社より引用
●それぞれの単元につき,くわしい「まとめ」と,入試過去問を掲載しています。問題を解いていてわからないことがでてきたら「まとめ」に戻ることができるリターン機能がついています。
●入試過去問は「基礎力アップ入試問題」「実力アップ入試問題」のステップ別に構成。自分の学習レベルに応じて問題を解くことができます。
●知識を問うだけでなく,考える力が試される問題を,「思考力活用編」として掲載しています。
●巻末に,力だめしができる「実力完成テスト」つき。
【おすすめする理由】
偏差値55くらいまでの高校を志望している人向けです。
中堅高校の入試問題を中心に、出題頻度のたかい問題を集めてくれています。
解けるようにしておくべき問題ばかりですから、非常に時間効率の受験勉強ができます。
『塾で教える高校入試 数学 塾技100 新装版』(難関校)

塾で教える高校入試 数学 塾技100 新装版 (高校入試 塾技)
出版社:文英堂
特徴:
学校では教えてくれない塾独自の「塾技」を学べる!
現役塾講師が、塾で教える「塾技」を公開!学校の教科書レベルから入試レベルまで引き上げます。入試で必要な内容を学年ごとに掲載!
学年・学習時期にそって内容を展開。入試をひかえた3年生はもちろん、少し早めに入試対策をしたいという1年生・2年生すべての生徒さんが活用できます。無理なく入試レベルの実力が身につく構成!
「塾技要点」→「塾技解説」→「入試問題をチェック!」→「入試問題にチャレンジ!」と入試レベルまで段階的な力の向上が可能です。入試最頻出分野の関数・図形問題が充実!
入試問題の6割以上を占める関数・図形分野を多く取り入れ、解答はできる限り図・表を用いてわかりやすく解説。入試で差がつく関数・図形分野の強化に最適です。巻末付録、例題付き公式集!
文英堂より引用
入試頻出の定理・公式を満載!「塾技」本文で紹介できなかったものも掲載しています。例題付きなので、定理・公式の確認後、例題を用いて活用法のチェックもできます。
【おすすめする理由】
偏差値60以上の高校を志望している人向けです。
教科書に載っていない応用問題の解法を教えてくれる問題集です。
時短テクニックなど、入試に役立つ解き方が満載です。
『最高水準問題集 高校入試 数学』(難関校)

最高水準問題集 高校入試 数学
出版社:文英堂
特徴:
難関高校の入試問題で実力強化
国立・私立難関高校の入試問題から質の高い良問を精選しました。トップレベルの実力を身につけることができます。難問・超難問も多数掲載
私立難関高校で出題された難問・超難問も多数掲載しています。超難関高校の入試対策は万全です。選択学習しやすい表示
文英堂より引用
各問題には1~3個の★でレベルを表示しています。また、入試によく出る問題には「頻出」マーク、とくに難しい問題には「難」マークをつけています。学習時間・実力に合わせた使い方ができます。
【おすすめする理由】
偏差値65くらいまでの難関高を志望している人向けです。
難関高校の入試問題から難問ばかり集められています。
時間的に効率よく難問対策できます。
1周目はかなりむずかしく感じる問題もあるはずです。
3周はするようにしましょう。
『国立高校・難関私立高校入試対策 上級問題集 数学』(難関校)

国立高校・難関私立高校入試対策 上級問題集 数学
出版社:旺文社
特徴:
この問題集は,国立高校や難関私立高校入試対策として,難易度が高い問題を収録しています。厳選されたハイレベルな過去問を解くことによって,入試を突破するための実力を着実に養えます。詳しい解説を収録した別冊解答も付いているので,解けなかった問題もその解き方を身につけることができます。最後には,実力を試せる模擬試験も収録しています
。旺文社より引用
【おすすめする理由】
偏差値65以上の高校を志望している人向けです。
難問、超難問が集まっています。
見たことがない問題もあるかもしれません。思考力が問われるので、非常に良い練習ができます。
この1冊で難関私立高校の入試対策は大丈夫です。
まとめ
高校入試の数学でよく出る問題をまとめました。二次方程式などの計算問題、比例・反比例と関数の問題、確率の問題、図形の問題です。いずれも必ず正解しておきたい問題ばかりです。
また、条件や性質を覚える、問題のパターン演習をするなどして入試に対応できる学力を養いましょう。
※関連記事:中学数学のハイレベル問題集(難関高校受験)
※Z会の中学生コースについて下記記事でくわしく紹介しています。
【中学生向け】Z会タブレットコースの進め方:成績上位を取って難関校に合格する方法を解説


コメント