中学校の数学にはいくつも単元がありますが、
なかでも多くの中学生が苦手にしているのは「図形」ではないでしょうか。
計算問題や文章問題、関数は得意なのに、
図形が出てくると急にテストの点数がさがる生徒はたくさんいます。
ですが、図形を得意にしておくと、
- 高校入試で得点源になる
- 高校数学を得意にしやすい
といったメリットを得られます。
そこで、数学の「平面図形」「空間図形」がわかるようになる勉強の仕方を紹介します。
※関連記事:関数、比例・反比例の問題の解き方
※関連記事:確率の問題の解き方
※関連記事:高校受験によく出る数学の文章問題10日分
この記事は下記の方向けです。
- 図形の定期テスト対策を知りたい方
- 高校入試に向けて図形を克服したい方
以下のリンクは難関受験に強いZ会の案内です。リンク先で資料請求ができます。
Z会 中学生コースの案内
図形の重要性
中学校の数学で、図形はかなり重要です。
図形は独立した分野ではなく、
方程式や関数とも関係しています。
数学は積み重ねの科目ですから、
関係している分野もきっちり解けるようにならないと、図形は解けるようになりません。
図形を克服するために図形だけがんばっても、なかなか成果を出せない場合もあるのです。
また、図形は解法を当てはめるだけでは解けない問題も多く、数学的なひらめきも求められます。
つまり、
- 数学の解法
- 数学のセンス
の2つを身に付けたかどうか問われるのです。
図形はいつ習うのか
図形は中学校でいつごろ習うのか確認します。
公立中学校の場合、下記の表のようになります。
| 学年 | 定期テストの時期 | 単元名 |
| 中学1年 | 【2学期制】 後期中間テスト・後期期末テスト 【3学期制】 2学期期末テスト・3学期学年末テスト | 「平面図形」 「空間図形」 |
| 中学2年 | 【2学期制】 後期中間テスト・後期期末テスト 【3学期制】 2学期期末テスト・3学期学年末テスト | 「平面図形と平行線の性質」 「図形の合同」 |
| 中学3年 | 【2学期制】 後期中間テスト・後期期末テスト 【3学期制】 2学期期末テスト・3学期学年末テスト | 「図形の相似」 「円周角と中心角」 「三平方の定理」 |
図形は各学年の後半、おおむね11月から年度終わりまで習います。
各学年の仕上げの時期に習うのです。
単元ごとのつながり(学習系統図)
図形はほかの単元とどうつながっているのか確認します。
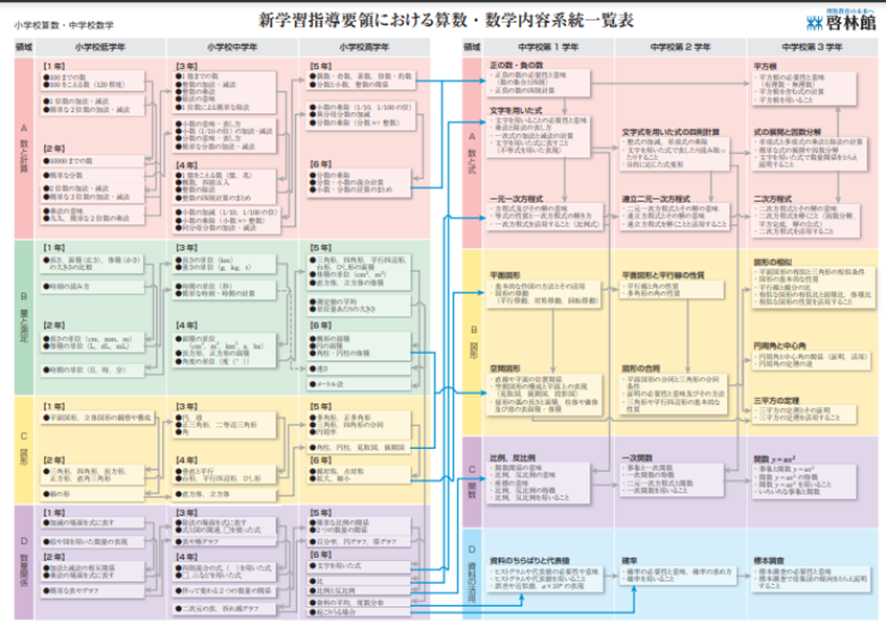
前項で確認したように、図形は各学年の仕上げの時期です。
それまで習ってきたほかの単元とつながっています。
【中学1年】
・「文字式」と「一次方程式」からつながってくる
・「平面図形」は中学2年の「平面図形と平行線の性質」につながっていく
【中学2年】
・連立方程式からつながってくる
・「図形の合同」は中学3年の図形範囲すべてにつながっていく
【中学3年】
・図形範囲の3単元がすべて高校の「図形と計量」につながっていく
どこか1つの単元が苦手になってしまうと、
その後に習うすべての単元に影響してしまいます。
習ったときに苦手意識を持ってしまったら、次の単元に入るまえに克服しておきたいですね。
空間図形の解き方
空間図形にはいくつもの単元があります。単元ごとに解き方のコツを紹介します。
直線や平面の位置関係
平行・垂直・ねじれの位置を習います。
空間図形の辺や角、対角線で平行・垂直・ねじれの位置の組み合わせを見つける問題が出てきます。
解き方のコツ
空間図形でのねじれの位置をイメージできるかどうかがポイントです。
自分の手指やシャーペンなどを使って平行や垂直、ねじれの位置を再現してみましょう。位置関係をイメージしやすくなります。
特にねじれの位置が分かりにくいかもしれません。
2週間ほどこまめにイメージする練習をすると脳が慣れてきます。
定期テストや入試では確実に正解しておきたい得点源になる範囲です。慣れるまで練習問題を繰り返しましょう。
角柱・円柱、角錐・円錐、球の特徴と表面積・体積
三角柱、四角柱、円柱と、
三角錐、四角錐、円錐の形の特徴を習います。
それぞれの空間図形を展開したらどうなるか(展開図)も学習します。
また、それぞれの表面積や体積を求める問題がよく出てきます。
| 体積の求め方 | 表面積の求め方 | |
| 三角柱 | 底面積×高さ (底辺×高さ×1/2×高さ) | 底面積×2+側面積(側面の四角形の面積をすべて足す) |
| 四角柱 | 底面積×高さ (たて×横×高さ) | 底面積×2+側面積(側面の四角形の面積をすべて足す) |
| 円柱 | 底面積×高さ (半径×半径×π×高さ) | 底面積×2+側面積(底面の直径×π×高さ) |
| 三角錐 | 三角柱の体積×1/3 | 底面積+側面積(側面の四角形の面積をすべて足す) |
| 四角錐 | 四角柱の体積×1/3 | 底面積+側面積(側面の四角形の面積をすべて足す) |
| 円錐 | 円柱の体積×1/3 | 母線の長さ×底面の半径× π |
| 球 | 4/3×π×r³(半径×半径×半径) | 4πr²(4×π×半径×半径) |
【扇形の弧の長さと面積、柱体や錐体及び球の表面積・体積】
角柱、四角柱、円柱と三角錐、四角錐、円錐の表面積・体積を求めます。
解き方のコツ
空間図形ごとの名称をきっちり覚えておきましょう。
柱と錐の区別をつけておくと、
覚えやすくなります。
- 柱:ずん胴な図形
- 錐:上がとんがっている
上記は数学的ではない書き方ですが、イメージしやすいと思います。
また、空間図形ごとの展開図がどのような形になるか覚えておきましょう。フリーハンドで描けるようにしておくとテストでも迷わず解けるようになります。
ここで展開図を覚えておくと、
表面積を求める問題がとても解きやすくなります。
相似
形が同じで大きさだけが違う図形どうしを「相似」と言います。
以下の3つの相似条件が出てきます。
上記の相似条件を使って証明問題を解きます。
また、相似比を使って辺の長さや面積を出す問題も出てきます。
相似の証明の解き方
相似の証明方法は2年生の合同の証明方法とよく似ています。
学習ポイントは2つです。
証明の書き方は5-10問も解くと慣れられますが、応用問題になると、使える相似条件を見抜くのがむずかしくなっていきます。
3つの相似条件を1つ1つ、その問題で使えそうかどうかを試します。
「もしこの相似条件を使うとしたら、どの辺や角が等しいと言えたらいいだろう?」
という考え方をすると、相似条件を見つけやすくなります。
相似比の解き方
相似比を求められれば、面積比と体積比も求められることを覚えておきましょう。
になります。
面積の単位はcm2で、
体積の単位はcm3ですね。
cmについてる2とか3を使うと覚えておくと便利です。
2なら2乗で、
3なら3乗です。
三平方の定理
三平方の定理は直角三角形で2つの辺の長さが分かっているときに残る1辺の長さを求めるときに使うものです。
公式を3種類覚えておきましょう。
一番代表的な公式は
「a2+b2=c2」です。
斜辺の2乗はほかの2辺の2乗の和に等しくなるという公式です。
また、特に下記のような三角形では辺の比が別に決まっています。
この定理を使って証明問題や関数の応用問題、図形の体積・面積の応用問題を解きます。
解き方のコツ
基本問題は前述の定理をそのまま当てはめるだけで解けます。
応用問題に入っていくと、三平方の定理をそのまま当てはめられない問題が出てきます。
三平方の定理以外に、ピタゴラス数(三平方の定理が成立する三辺の比)を覚えておくと便利です。
- 3 : 4 : 5
- 5 :12 : 13
- 8 :15 : 17
- 7 : 24 : 25
また、中3の3学期に出てくる応用問題や高校入試の図形と関数の融合問題では、「どうせ三平方の定理を使うんでしょ」と、「決め打ち」で大抵解けます。
直角三角形があれば三平方の定理を使えるので、「どこかに垂線を引いて三平方の定理を使えないかな?」という視点で問題を解いてみましょう。
平面図形の解き方
つづいて、平面図形の学習内容と解き方のコツを紹介します。
作図
コンパスを使って、
垂直二等分線と角の二等分線を習います。
解き方
作図のパターンは限られています。
垂直二等分線は3パターン、
二等分線は1パターンの、
合計4パターンだけです。
どのパターンがどういう描き方になるか意識しながら描いて練習しましょう。
図形の移動(平行移動・対象移動・回転移動)
線分、垂直、平行の用語の定義と、
平行移動・対象移動・回転移動した場合の三角形の動き方を習います。
解き方
平行移動・対象移動・回転移動の「移動の仕方」をそれぞれ覚えておきましょう。
移動の仕方を区別できれば、テストでは高得点をねらえる範囲です。
角度
中2で、三角形や平行線でつくる角度を求める単元が出てきます。
中3の図形や高校入試の問題でもよく使う内容です。
平行線と角の性質の解き方
対頂角、同位角、錯覚の定義をきっちり覚えておきましょう。
- 対頂角:2つの直線が交わってできる角のうち、互いに向かい合っている角
- 同位角:1つの直線に2つの直線が交わってできる角のうち、同じ位置にある1組の角
- 錯覚:1つの直線に2つの直線が交わってできる角のうち、斜め向かいの位置にある1組の角
また、平行線な2直線の間に平行な補助線を引く方法を覚えましょう。
定期テストに出てくる平行線の角度のほとんどの問題は、補助線を引くと正解できます。
多角形の角の性質の解き方
多角形の内角の和と外角の求め方を覚えておきましょう。
- 内角の和:180×(n-2)
- 外角の和:360°
- 内角と外角の和:180°
この3つの性質・計算方法を使って問題を解きます。
問題のパターンは限られていますから、
問題を解くときに、ほかのページのどの問題と同じパターンなのかを確認するようにしてみましょう。
もし解き方がわからなくても、
上記の3つの性質・計算方法を1つ1つ試していけば、答えが出やすくなります。
合同
三角形や四角形の合同を証明する問題が出てきます。
合同とは、同じ形・同じ大きさの図形であるということです。
解き方
三角形・直角三角形の性質と、
三角形の合同条件をきっちり覚えておきましょう。
合同条件:
- 1組の辺とその両端の角がそれぞれ等しい
- 2組の辺とその間の角がそれぞれ等しい
- 3組の辺がすべて等しい
辺の組み合わせ数や角の数で覚えると思い出しやすいです。
表にすると、下記のようになります。
| 1組の辺とその両端の角 | 2組の辺とその間の角 | 3組の辺 | |
| 対応する辺の数 | 1 | 2 | 3 |
| 対応する角の数 | 2 | 1 | 0 |
| 辺と角の数の合計 | 3 | 3 | 3 |
3つのうちどれか1つを覚えておけば、
あとの2つを思い出しやすくなります。
「辺が1組等しいと証明できるなら、角は2つ証明すればいい」とわかります。
また、証明問題は「三角形ABCと三角形DEFにおいて~」のような、独特の書き方に戸惑うかもしれません。
最初は違和感があるでしょうが、
5-10問解いているうちに慣れてきます。
合同条件を使って証明するには、
注意が必要です。
合同条件を言うためには「なんとなく」ではなく、三角形・直角三角形や平行などの性質を正しく使う必要があります。
「直角に見えるからこの三角形は直角三角形だ」
としてしまいたくなりますが、
問題の条件から確実にそうだと言える場合に限定しないといけません。
この点を意識しておけば、定期テストの合同の証明はクリアできます。
平行線と線分の比
平行線にはさまれた線分の比は等しいという性質を習います。
下記のような図では、a:a’=b:b’になります。
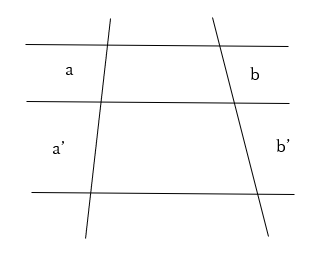
解き方
この範囲の学習ポイントは2つです。
比例式は、辺の長さの比を比べる式です。
AB : CD = EF : GH
のとき、
AB=5cm、CD=2cm、EF=10cm
なら、
5 : 2 = 10 : GH
という式になります。この式を解いて、
5 ×GH = 2 × 10
GH = 4(cm)
のように、辺GHの長さを求めます。
慣れれば単純で、なんなら比例式をつくらなくても解けるようになります。
比例式を得意にするのが、この単元を得意にする近道です。
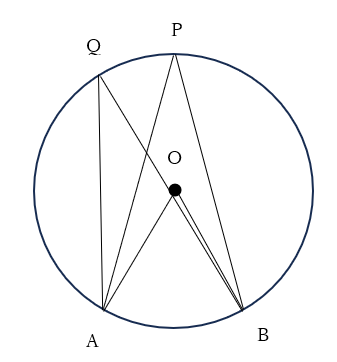
円習角と中心角
同一の弧の場合、中心角は円周角の2倍になるという内容です。
下記のような図で、「∠APB=1/2∠AOB」になります。
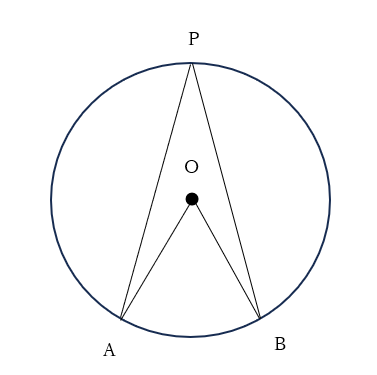
∠APBが円周角、∠AOBが中心角です。
また、同じ弧なら円周角は同じ大きさになります。
下記の図では、∠APB=∠AQBです。
解き方
まず、円周角の定理を覚えておきましょう。
また、この定理の逆や、他の性質も覚えておくと便利です。
この5つの定理や性質(定理の逆)を使って応用問題を解きます。
応用問題はパターンが限られています。
大きく分けて下記の2パターンで解きます。
平面図形・空間図形の応用問題の解き方
平面図形や空間図形の応用問題は、一見するとややこしい形をしています。
ですが、解答の仕方にはコツがあります。
平行や直角を探す
まず、図形のなかで平行や直角がないか探しましょう。下記のような性質を利用できます。
四角形のなかで「平行な2本の直線」を見つけるのは、慣れるまで苦労する子が多いです。長方形や平行四辺形がかくれていないか探すと見つけやすいです。
特に、平行四辺形であれば平行・辺の長さが等しいの両方の条件が使えて便利です。
平行や直角になる直線を引く
平行や直角が見つからない(それらしい四角形もない)場合、平行や直角になる直線を引きましょう。
応用問題では、与えられた図形に垂線を引くなどして解く問題が大半です。「どこかに線を引くんでしょ?」という前提で問題を解きましょう。
二等辺三角形や直角三角形を探す
平行以外にも、二等辺三角形や直角三角形がないか探してみましょう。下記のような性質を利用できます。
二等辺三角形や直角三角形ができる直線を引く
こちらも、二等辺三角形や直角三角形が見つからなければ直線を引いて二等辺三角形や直角三角形をつくってしまいましょう。
特につくりやすいのは直角三角形です。垂線を引けば直角三角形のできあがりです。
三平方の定理を使ってみる
ほかにも、中3の3学期以降に出てくる問題や高校入試の応用問題では「三平方の定理」を使って解く問題が非常に多いです。
特に「辺の長さを求める問題」ではほぼ三平方の定理を使います。
「全然解き方がわからない…」といいう場合には、とりあえず三平方の定理を使って辺の長さを求めてみましょう。
そこから二等辺三角形や平行四辺形が見つかって解答にたどりつけるパターンが多いです。
数学の定期テスト対策でおすすめの問題集
定期テスト対策でおすすめの問題集を紹介します。いずれもAmazonのPRリンクをつけているので、リンク先でお得に購入いただけます。
テストで平均点を目指せる数学の問題集
まずは数学が苦手な人向けの問題集です。
『中2数学の図形の証明―定期テストに自信がもてる! (これでだいじょうぶ!シリーズ) 』
最初に紹介するのはくもんの「これでだいじょうぶ」シリーズです。
図形の証明問題に絞って基礎からじっくり練習できます。定期テストで平均点を目指す人、図形に苦手意識を持っている人におすすめです。

中2数学の図形の証明―定期テストに自信がもてる! (これでだいじょうぶ!シリーズ)
出版社:くもん出版
難易度:易(★☆☆)
『できた!数学 関数・図形・データの活用(中1~中3)』
つづいて紹介するのはくもんの「できた!」シリーズです。
学年ごとに、学校で習う順番どおり前半と後半に2冊ずつに分かれています。定期テストの問題と同じレベルの演習問題が並んでおり、テスト対策に使いやすいです。
こちらで紹介しているのは「後半部分」です。
中1向け↓

できた!中1数学 関数・図形・データの活用 (中学基礎がため100%)
中2向け↓

できた!中3数学 図形・データの活用 (中学基礎がため100%)
中3向け↓

できた!中3数学 図形・データの活用 (中学基礎がため100%)
出版社:くもん出版
難易度:易~標準(★★☆)
特徴:
〔本書のねらい〕
基礎・基本が最初の一歩からよくわかるくもん独自のステップで,解きながら学ぶことができます。また,4択クイズアプリにより,テスト前にスマホで5教科の要点チェックができます。〔学習内容・特徴〕
くもん出版より引用
①基礎からのスモールステップと反復練習により,無理なく学習が進められます。
②豊富な練習量でなめらかなステップを実現することで,基礎力を確実に身につけます。
③未知のことを一方的に「教わる」のではなく,「例」や「空欄問題」を見て解き進めながら,自ら学びとることができます。
④発展的な問題も含んでいるので,高校入試対策の第1段階としてのベース作りができます。
⑤見やすい2色の解答・解説で「考え方」を確認し,理解を深めます。
『中学定期テスト 得点アップ問題集 改訂版(中1~中3)』
つづいては旺文社の「得点アップ問題集」シリーズです。こちらも定期テストの問題と同じくらいの問題集演習が並んでいます。
特徴は、テスト前の1週間で対策できるような分量にしているという点です。
1日ごとにこのページを勉強しましょうと分けてくれており、「どこから勉強すればいいか」「どれくらい勉強すればいいか」を考える必要がありません。
中1向け↓

中学定期テスト 得点アップ問題集 中1数学 改訂版
中2向け↓

中学定期テスト 得点アップ問題集 中2数学 改訂版
中3向け↓

中学定期テスト 得点アップ問題集 中3数学 改訂版
出版社:旺文社
難易度:易~標準(★★☆)
特徴:
中学校の定期テスト対策を、1日30分×7日間を目安として短期完成できる問題集です。
■各単元の構成は、STEP1要点チェック・STEP2基本問題・STEP3得点アップ問題の3ステップで、段階的に定期テストの得点力が身につきます。
STEP1 要点チェック 単元の大事な学習ポイントをまとめています。
STEP2 基本問題 基本的な問題で単元の内容を確認できます。
STEP3 得点アップ問題 定期テストの問題形式にならった単元の総仕上げ問題です。■スケジュールの目安が示してあるので、定期テストの範囲を1日30分×7日間で、計画的にスピード完成できます。
旺文社より引用
■コンパクトで持ち運びしやすい別冊「+10点暗記ブック」&赤セルシートで、いつでもどこでも、テスト直前まで大切なポイントを確認できます。
80点以上を目指せる数学の問題集
つづいて、テストで80点、90点以上を取りたい人向けの問題集を紹介します。
80点以上を目指すなら、
応用問題を解けるかどうかがポイントになります。
前述の学習ポイントをすべて押さえておくと80点を取る実力が身につきます。
テストでミスをしない・制限時間内に解く力を養いましょう。
『チャート式 中学数学』(中1~中3)
最初は「チャート式」です。
参考書編と問題集編に分かれており、参考書編は単元のポイントを丁寧に解説して理解しやすくしています。参考書編をみながら問題集編を解くと、「どこを参照すれば良いか」が分かりやすく勉強しやすいです。
どの学年も1冊200ページ以上もあり、問題量が豊富です。
中1:参考書編↓

チャート式 中学数学 1年
中1:問題集編↓

チャート式 中学数学 1年 準拠ドリル (チャート式・シリーズ)
中2:参考書編↓

チャート式 中学数学 2年
中2:問題集編↓

チャート式 中学数学 2年 準拠ドリル (チャート式・シリーズ)
中3:参考書編↓

チャート式 中学数学 3年
中3:問題集編↓

チャート式 中学数学 3年 準拠ドリル (チャート式・シリーズ)
出版社:数研出版
難易度:標準~難(★★★)
特徴:
日常学習から入試対策まで充実の1冊!
教科書の内容からていねいに説明し,公立高校入試レベルまで着実に力をつけることができる参考書。
数研出版より引用
考え方や問題の着眼点,注意事項などをていねいに説明し,思考力を養うことができる。単元の要点を説明する解説動画や,計算問題をカード形式で反復練習できる計算カードなど,デジタルコンテンツを利用した学習ができ,自学自習にも最適。入試対策編では入試頻出の問題をおさえてから,入試レベルの問題に取り組むことができる。
数学を苦手にしている中学生から実力UPを目指す中学生まで多くの中学生にオススメ。
『最高水準問題集 特進 中1/中2/中3数学』
つづいては「最高水準問題集」です。
タイトルどおり、難易度の高い問題中心の問題集です。定期テストで出てこないようなハイレベルな問題も掲載されています。
そうした発展問題も解けるようにしておくと、定期テストでミスをしにくくなります。
中1用はコチラ↓

最高水準問題集 特進 中1数学
中2用はコチラ↓

最高水準問題集 特進 中2数学
中3用はコチラ↓

最高水準問題集 特進 中3数学
出版社:文英堂
特徴:
難関高校の入試問題で実力強化
国立・私立難関高校の入試問題から質の高い良問を精選しました。トップレベルの実力を身につけることができます。難問・超難問も多数掲載
私立難関高校で出題された難問・超難問も多数掲載しています。超難関高校の入試対策は万全です。選択学習しやすい表示
文英堂より引用
各問題には1~3個の★でレベルを表示しています。また、入試によく出る問題には「頻出」マーク、とくに難しい問題には「難」マークをつけています。学習時間・実力に合わせた使い方ができます。
図形分野の高校入試対策の仕方
入試対策をするときは、以前習った内容を少し忘れてきていると思います。まずは単元別の復習から入りましょう。
入試頻出パターンごとに勉強する
入試問題は出題パターンが限られています。よく出るパターンごとに勉強すると効率よく得点アップにつなげられます。
入試に基本問題は出ないので、
単元別の復習をしたら早速入試対策に入りましょう。
頻出パターンごとの勉強方法をお伝えします。
合同・相似の証明と線分比を解くコツ
1つ目は、合同・相似を使う応用問題です。
下記の条件や性質を使うことが多いです。
- 合同条件・相似条件
- 平行線の性質(対頂角など)
- 線分比、面積比、体積比
問題を見たら、この条件・性質のどれを使えそうか当てはめてみましょう。
線分比を使って辺の長さを求める問題は難易度が高く、難関高志望者以外は「捨て問」にしてしまって大丈夫です。
難関高志望者は正解しておきたいところです。
問題用紙に描かれている図をそのままでは使えません。
線を描きなおしたり補助線を引いたりして、
相似比が使える図形に描きかえましょう。
角度を解くコツ
角度を求める問題が頻出です。下記の性質や定理を使うことが多いです。
- 平行線の性質(対頂角など)
- 円周角の定理とその逆
平行線が1つのカギになります。図に平行線が描かれていなければ、自分で描くようにしてみましょう。
入試に出る図形問題のほとんどが平行線を描けば解けるものです。「どこかに平行線を引くはずだ」と決め打ちで解いてみましょう。
作図を解くコツ
作図問題はバリエーションが少なく、基本問題が多いです。必ず正解しておきたいですね。
使う解法は下記の2つです。
- 角の二等分線
- 垂直の二等分線
作図は問題パターンが特に少ないです。「今自分が解いている問題は角の二等分線と垂直の二等分線のどちらの問題なのか」を意識しながら解くようにしましょう。
高校入試数学のおすすめの問題集
中学3年生の長期休み(春・夏・冬)には、
高校入試対策をしておきましょう。
おすすめの高校入試対策問題集を紹介します。
志望校の難易度によって問題集は変えるようにしましょう。
『高校入試「解き方」が身につく問題集 数学』
数学は解法だけでなく「なぜその解き方をするのか?」という「考え方」を大事にすると伸びやすくなります。
この問題集はそういう「解き方(考え方)」をしっかりと解説してくれている問題集です。
ほかの問題集で「解説を読んでも、解く手順は分かるけどなぜそう解くのかピンとこない」という人におすすめです。

高校入試「解き方」が身につく問題集 数学
出版社:旺文社
特徴:
「暗記では解けない問題の解き方」を身につける!
★「出題頻度が高い」&「解き方にコツがある」問題をマスターして得点アップ!
公立高校入試の問題は、難度の幅が広く、暗記で解ける問題と解き方(考え方)が必要な問題があります。一部の問題は演習量よりも、解き方を押さえてから演習したほうが効率的に点数を上げることができます。本書で選んだ問題をマスターすることで、入試の得点アップにつながります。★徹底的に「解き方」に焦点を当てた解説!
旺文社より引用
「例題」「解き方チェック問題」「実践問題の解答解説」のすべてで「解き方」のチェックポイントに沿った解説をしています。
『高校入試 ニガテをなんとかする問題集 数学 改訂版』
つづいては旺文社の「ニガテをなんとかする」シリーズです。
長い問題文の読み方のコツ、受験生が間違いやすい問題パターンを集めての演習など、「受験生のニガテ克服」に特化した問題集です。

高校入試 ニガテをなんとかする問題集 数学 改訂版
出版社:旺文社
特徴:
高校入試に向けて,苦手分野を克服するための問題集です。
Amazonより引用
各単元は,受験生が苦手意識を持ちやすい「ニガテパターン」+「攻略法」で構成されています。
「攻略法」はニガテな人でも実践できるよう,わかりやすいものを掲載しています。
ニガテの種類がひとめでわかる,「ニガテマップ」つき。
『きちんとこれだけ公立高校入試対策問題集 数学』
こちらの問題集は、「公立高校入試向けに標準レベルの問題ばかり」を集めた問題集です。
入試数学では難易度の高い問題も出てきますが、ライバルと差が開くのはむしろ「標準レベルの問題」です。50%以上の受験生が正解できるレベルの問題を100%正解すれば、それだけでライバルより10点程度高い点数を取れます。

きちんとこれだけ公立高校入試対策問題集 数学 改訂版
出版社:旺文社
特徴:
全国の公立高校入試の配点データを分析し、中配点・中難度の過去問に厳選した問題集です。学習効果が最も出やすい「標準問題」を確実に解く力をつけることを目的として、各課を「要点まとめ + 過去問演習」で構成し、理解と定着を交互に行うことができます。
以下のような方に特におすすめです。
旺文社より引用
・公立高校を第一志望にしている。
・基本事項ならある程度は覚えている。
・全範囲をまんべんなく解けるようになりたい。
・1冊の問題集をやり切って実力をつけたい。
『チャート式 難関校受験対策 ハイレベル中学数学問題集』
人気のチャート式問題集でです。
公立高校入試レベル~難関国公立・私立高校入試レベルまでカバーしています。
全50回のテストで段階的に学力を伸ばせる設計なので、何度も間違う苦手単元の発見にも役立ちます。

チャート式 難関校受験対策 ハイレベル中学数学問題集
出版社:数研出版
特徴:
難関高校を受験する人に最適な、入試本番を見据えた実戦的な問題集。
Amazonより引用
問題はランダム配列で、1回5問の実戦テスト形式です。目安時間もあるため、本番を意識した実戦的な勉強ができます。問題のレベルによって「標準」「発展」「難関」の3段階のコースに分かれており、実力に応じた演習が可能です。標準は15回分の公立高校入試レベル、発展は15回分の中堅私立高校入試レベル、応用は20回分の難関国公立・私立高校入試レベルの問題を掲載しています。別冊解答編には、問題の答のほか問題の考え方や詳しい解説を掲載しています。解法の過程を確実に押さえることで、難問に対するアプローチの仕方が身につきます。本冊112ページ、解答編152ページ。
『最高水準問題集 高校入試 数学』
この問題集は難関国立・難関私立高校入試対策の定番です。
発展問題中心に構成されており、定期テストで80点以上を取っている人でようやく少しずつ使いこなせるレベルです。
各問題に「難」「頻出」「新傾向」とマークをつけてくれているので、自身の志望校の入試問題にあわせて選択できます。
単元別問題で弱点を補強しておき、
チェックを兼ねて総合問題で仕上げができます。
難問ぞろいなので、初見で解けない問題もたくさんあります。

最高水準問題集 高校入試 数学
出版社:文英堂
特徴:
過去の入試問題を徹底分析
国立・私立難関高校の入試問題を全分野から厳選。よく出る問題には「頻出」マークを、特に難しい問題には「難」マークをつけて、問題を解きながら、問題のレベルや傾向がわかるように配慮しました。重点的に強化できる単元別の配列
各自の学習計画に合わせてどこからでも学習できます。また弱点分野の補強や、入試直前の重点演習もできます。入試対策総仕上げのための模擬テスト
文英堂より引用
入試本番を想定した模擬テストを巻末につけました。志望校突破のための最終チェックができます。
※関連記事:数学80点以上の人向けおすすめ問題集と勉強方法
図形のおすすめアプリ
「空間図形の切断面がイメージできない」
「あの公式なんだっけ…?」
ということありますよね。
そんなときに便利な無料アプリを2つ紹介します。
立体学習あぷり Lite

Appストアでみる
評価:Appストア3.5
課金要素:無料
※広告表示あり
スクリーンショット:
特徴:
立体を理解するのに役立つアプリです。頭の中で考えるのも、紙に描くのもちょっと難しい図形問題。
例えば、「立体を切ったら、切り口はどんな形?」、「この立体を展開したらどうなる?」などの疑問に対し、実際に立体を切ったり、展開したりすることができます。
有料版なら、円柱・円錐の展開や、さらに長さや面の面積、立体の体積をアプリに計算させたり、印刷したり、面に線を引いたりすることもできます。
Appストアより引用
【おすすめ理由】
立体図形を切ったときにどうなるかを、
試しながら確認できます。
紙の教材でイメージしづらいときに大活躍します。
数学公式集

Appストアでみる
Google Playでみる
評価:Appストア4.6、Google Play4.3
ダウンロード数:10万以上
課金要素:無料
※広告表示あり
スクリーンショット:
特徴:
中学数学、高校数学の重要公式をカンタンに確認できるアプリが新登場!
各公式ページについている、公式の利用シーン、公式の覚え方・使い方などの、お役立ち解説は必読!
このアプリで中学数学、高校数学の重要公式をしっかり確認しよう!公式は、中学数学(数と式、関数、図形)、高校数学(数学Ⅰ、数学A、数学Ⅱ、数学B、数学Ⅲ)の分野別に収録。
アプリ内の検索機能で公式を検索することもでき、とても便利です。本アプリ「数学公式集(中学数学・高校数学の公式解説集)」は無料です。
収録内容について何かあれば、アプリ内のお問い合わせからご連絡ください。
Appストアより引用
【おすすめ理由】
ふと公式を忘れたときに役立ちます。
公式の使い方も解説してくれます。
無料で利用できるのもありがたいです(広告表示あり)。
まとめ
いかがでしょうか。
中学生向けに図形の解き方を紹介しました。
平面図形・空間図形が苦手な中学生は多いです。
覚えないといけない公式や定理・性質がたくさんあり、
問題を解くときにこんがらがってしまいます。
ですが高校入試には頻出単元ですし、複数の定理・性質を組み合わせないと解けない応用問題もほぼ必ず出てきます。
※関連記事:高校受験によく出る数学の文章問題10日分
※関連記事:高校入試の数学でよく出る問題(計算、関数、確率、図形)
単元ごとのポイント解説、日ごろの定期テスト対策・受験対策の仕方を解説し、おすすめの問題集とアプリを紹介しました。
※定期テスト対策、高校入試対策についてこちらの記事もどうぞ
数学の定期テスト対策の問題集17選
数学の定期テスト対策の仕方市販の参考書・問題集を使っての学習がはかどらない場合は、通信教育もおすすめです。
3D動画で解説してくれる通信教育もあり、Z会など難関高入試対策を得意にしている通信教育もあります。ほかにも、偏差値30からの入試対策が得意なすららなど、以下の記事で大手通信教育5社を比較しています。
【トップ高を目指している方にはZ会がおすすめです。下記のPRリンクからZ会に資料請求ができます。】
【中学生のためのZ会の通信教育】


コメント