【割合の問題】中学入試によく出る問題と勉強法：割合対策のおすすめ問題集

Pocket

「割合が苦手でいつも苦労している」
「集中的に割合の対策をして得意になりたい」

このような子どもはたくさんいますよね。

割合は受験算数のなかで1、2を争うほど重要な単元です。

※関連記事：【中学受験】割合の問題の解き方：苦手克服のコツ

そこで、中学入試の算数によく出る割合の問題をまとめました。問題と解説をセットにしていますので、演習しながら割合を得意にしていきましょう。

オーソドックスな入試問題以外にも思考力問題の対策問題もつけています。

また、割合をさらに対策したい人向けに、割合対策のおすすめ問題集も紹介します。

【下記リンクは難関中学受験対策で定番のZ会のPRです。クリックいただくと、Z会に無料の資料請求ができます。】

Ｚ会の通信教育　中学受験コース

※Z会の中学受験コースのメリットや活用法を下記の記事で紹介しています。
Z会中学受験コースだけで難関中学に合格する方法

中学入試：割合の問題①（小4～小5向け）
1. 問題①の解答
中学入試：割合の問題②（小5～小6向け）
1. 問題②の解答
中学入試：割合の勉強におすすめの問題集（基礎、難関）
割合を得意にする勉強方法3つ
中学受験算数の苦手を克服する方法
ほかの科目の勉強方法・問題
1. 関連

中学入試：割合の問題①（小4～小5向け）

問題1. 次の問題を解いてください。

(1)100円の20%はいくらですか。

(2)250円の3割はいくらですか。

(3)300円の2割5分はいくらですか。

(4)2mのひものうち2割を切ると、残りは何mになりますか。

(5)400gの40%は2kgの何%か。

(6)800円の6割は、何円の80%か。

(7)ミカンが何個かあった。80%を子どもにわけたところ、5個残った。ミカンは最初何個あったか。

(8)かおるさんは毎日歩いて学校にかよいます。晴れの日は家から学校まで15分かかります。雨の日は晴れの日の1.2倍かかります。明日は8時に学校につくように家を出たいのですが、明日の天気よほうは雨です。何時までに家を出れば8時に学校につきますか。

(9)落とした高さの30%はね上がるボールがあります。このボールを2m50cmの高さから落とすと、何cmはねあがりますか。

(10)けんいちろうくんは、もっているお金の40%にあたる800円で本を買いました。のこったお金の20%で消しゴムを買いました。消しゴムの代金はいくらでしたか。

(11)近くのショッピングモールでセールをしています。すべての商品を1つずつ買うとき、平日・休日どちらで買うほうが安くなりますか。ただし、消費税(しょうひぜい)は考えない。

【セール内容】
平日：500円以上の商品は20%オフ
休日：全品1割引き
【商品】
ポストイット：120円
えんぴつ（5本）：300円
ペンケース：550円

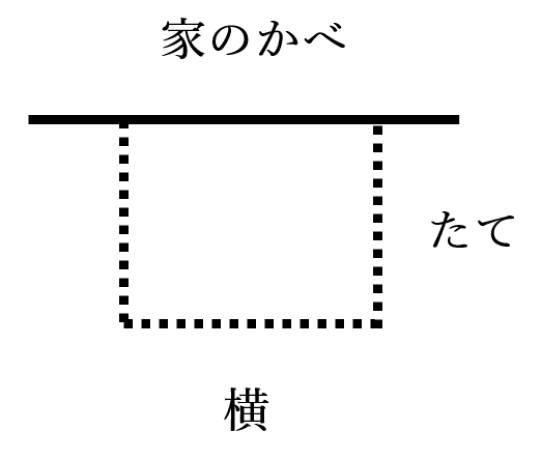
(12)長さ1mの棒(ぼう)が20本あります。下図のように、家のかべをつかって花だんをつくります。このとき、花だんの面積(めんせき)をできるだけ大きくするには、たて・横の長さをそれぞれ何mにすればいいでしょうか。

(13)1回の入場料(にゅうじょうりょう)が400円の動物(どうぶつ)園(えん)があります。5回分のチケットが1割引きで売られています。この5回分のチケットを1割引きで買いました。1回あたりいくらで入場(にゅうじょう)できることになりますか。

(14)姉のこづかいの80%は妹のこづかいより200円多いです。200円が妹のこづかいの25%にあたるとき、姉のこづかいは妹のこづかいよりいくら多いですか。

(15)あるクラスで算数の好きな人は全体の60%で、そのうち50%にあたる9人は国語も好きです。クラス全体で何人いますか。

問題①の解答

(1)答え：20円
100円×0.2=20円
※20%=0.2

(2)答え：75円
250円×0.3=75円
※3割=0.3

(3)答え：75円
300円×0.25=75円
※2割5分=0.25

(4)答え：1.6m
2m×0.2=0.4m…切ったひもの長さ
2m-0.4m=1.6m…残ったひもの長さ

(5)答え：8%
400g×0.4=160g…400gの40%の重さ
160g÷2000g×100=8%
※2kg=2000g
※%で表すには100倍する

(6)答え：600円
800円×0.6=480円…800円の6割
480円÷0.8=600円
(7)答え：25個
5個÷0.2=25個
※80%をわけたので、残りは20%=0.2

(8)答え：7時42分
15分×1.2=18分…雨の日に学校につくまでにかかる時間
※8時の18分前に家を出れば、8時に学校につく

(9)答え：75cm
250cm×0.3=75cm

(10)答え：240円
800円÷0.4=2000円…最初にもっていたお金
2000円-800円＝1200円…本を買ったあとに残ったお金
1200円×0.2=240円

(11)答え：休日
【平日に買った場合の合計代金】
※300円以上は20%引き=80%の代金になる
ポストイット：120円
えんぴつ（5本）：300円
ペンケース：550円×0.8=440円
合計：860円

【休日に買った場合の合計代金】
※全品1割引き
ポストイット：120円×0.9=108円
えんぴつ（5本）：300円×0.9=270円
ペンケース：550円×0.9=495円
合計：873円

(12)答え：たて：5m、横： 10m

たて（本）	1	2	3	4	5	6	7	8	9
横（本）	18	16	14	12	10	8	6	4	2
面積（m²）	18	32	42	48	50	48	42	32	18

※たては2辺あるが、横は1辺だけ（家のかべを使うから）
※1本で1mなので、たては5本＝5m、横は10本＝10m

(13)答え：324円
400円×5回×0.9=1800円…5回分のチケットの代金
1800円×0.9=1620円…5回分のチケットをさらに1割引きで買ったときの代金
1620円÷5回=324円

(14)450円
200円÷0.25=800円…妹のこづかい
(800円+200円)÷0.8=1250円…姉のこづかい
※姉のこづかいの80%が、妹のこづかい800円より200円多い金額
1250円-800円＝450円

(15)答え：30人
9人÷0.5=18人…算数が好きな人の人数
18人÷0.6=30人
※算数が好きな人（18人）はクラス全体の60%

中学入試：割合の問題②（小5～小6向け）

(1)かおるさんが算数・国語・理科・社会のテストを受けました。結果は、算数が80点、国語が90点、理科が75点でした。4教科の平均点が80点以上になるようにするには、社会で何点以上取ればいいですか。

(2)かおるさんがまた算数・国語・理科・社会のテストを受けました。結果は、算数・国語・理科の平均点が82点、算数・国語・社会の平均点が84点でした。理科と社会の平均点が86点でした。このとき、理科の点数は何点でしたか。

(3)ある本を全体の6割より20ページ少なく読んだところ、140ページ残りました。この本は全体で何ページありますか。

(4)算数の宿題を全体の8割より2問多く解いたところ、14題残りました。解き終わった問題の答え合わせをしたところ全体の2割を間違えていました。翌日に間違えた問題を解きなおしたうえで、残りすべての問題を解きました。間違い直しを含めて全部で何問解きましたか。

(5)ある地域の年齢別人口を調査したところ、18歳未満が全体の40%より20人多く、18歳以上が全体の55%より5人多いとわかりました。この地域に住む人口は何人ですか。

(6)あるスーパーでリンゴを80個仕入れました。1日目は、仕入れた個数の4割より2個少ない数のリンゴが売れました。2日目は残りのリンゴの8割が売れました。残りのリンゴはいくつですか。

(7)あるスーパーでリンゴを120個仕入れました。1日目は、仕入れた個数の3割より4個多く売れました。残ったリンゴのうち1割が痛んでいたのでジュースにしたところ、完売しました。2日目は残ったリンゴの5割が売れました。ジュースにしたリンゴを含めて、売れたリンゴの数はいくつですか。

(8)ある日のバスの利用者数を調べたところ、大人は全体の7割で、子どもは大人の5割より6人少ない人数でした。この日のバスの利用者数は全部で何人でしたか。

(9)ミカン80個を箱買いしました。兄・姉・弟の3人で3日後には食べ終わりました。3人食べたミカンの数は、姉は兄の2倍より4個多く、弟は兄の3倍より4個多かったです。兄は何個食べましたか。

(10)原価 2000円の商品を10個仕入れて4割の利益を見込んで売ったところ、1個売れ残った。利益はいくらになったか。

(11)原価50円のリンゴを200個仕入れて8割の利益を見込んで売ったところ、初日は3割売れた。2日目は定価の2割引きで売ったところ、すべて売れた。利益はいくらになったか。

(12)あるスーパーで原価50円リンゴを2000個仕入れ、8割の利益見込んで売ることにしました。1日目は、仕入れた個数の4割売れました。残ったリンゴのうち1割が痛んでいたのでジュースにしたところ合計5000円で売れました。2日目は残ったリンゴを定価の2割引で売ったところ、売り切れました。ジュースにしたリンゴを含めて、利益はいくらですか。

(13)【思考問題】ある商品がある。この商品に6割の利益を見込んで売ると完売するが、7割の利益を見込んで売ると1割が売れ残るという過去のデータがある。6割の利益を見込んで売る場合と7割の利益を見込んで売る場合のどちらのほうが多くの利益を見込めるか。

(14)はじめ、兄は3000円、妹は2000円のお金を持っていましたが、2人とも同じだけ使ったので兄と妹のお金の比は5:3になりました。2人は何円ずつ使いましたか。

(15)はじめ、姉は200枚、妹は120枚のシールを持っていましたが、姉が妹に何枚かあげたので、姉と妹のシールの枚数の比が3:5になりました。姉は妹に何枚あげましたか。

問題②の解答

(1)答え：75点以上
80点＋90点＋75点=245点
…3教科の合計得点
80点×4教科=320点
…平均80点以上取るために必要な4教科の合計得点
320点-245点=75点

(2)答え：83点
82点×3教科＝246点
…算数＋国語＋理科の合計得点
84点×3教科=252点
…算数＋国語＋社会の合計得点
252点-246点=6点
…社会のほうが理科より6点高い
(86点×2-6)÷2=83点
…社会を理科と同じ得点にして、1教科あたりの点数を算出

(3)答え：300ページ
140ページ-20ページ=120ページ
…本を全体の6割読んだ場合の残りのページ数
120ページ÷(1-0.6)=300ページ
…120ページは全体の4割にあたる

(4)答え：80題
14題＋2題=16題
…全体の8割を解いた場合の残りの問題数
16題÷(1-0.8)=80題
…16題は全体の2割にあたる

(5)答え：500人
20人+5人=25人
1-(0.4+0.55)=0.05
…40%と55%で合わせて95%。25人で全体の5%にあたる。
25人÷0.05=500人

(6)10個
80個×0.4-2個=30個
…1日目に売れたリンゴの数
80個-30個=50個
…1日目に売れ残ったリンゴの数
※最初の式を「80×(1-0.4)-2」にすると1回の計算で済みます
50個×0.8=40個
…2日目に売れたリンゴの数
50個-40個=10個
※「50×(1-0.8)」にすると1回の計算で済みます

(7)答え：84個
120個×3割+4=40個
…1日目に売れたリンゴの数
120個-40個=80個
…1日目に売れ残ったリンゴの数
※最初の式を「120×(1-0.3)+4」にすると1回の計算で済みます
80個×0.1=8個
…ジュースにしたリンゴの数
80個-8個=72個
…8個のリンゴをジュースにした後に残ったリンゴの数
※「80×(1-0.9)」にすると1回の計算で済みます
72個×5割=36個
…2日目に売れたリンゴの数
40個+36個＋8個=84個

(8)答え：120人
0.7×0.5=0.35
0.7+0.35=1.05
…全体の0.05(5%)が6人にあたる
6人÷0.05=120人

(9)答え：12個
兄の数を①とすると、
姉の数は①×2+4
弟の数は①×2+4と表せる。
兄＋姉＋弟
=①+②+4個+③+4個
=⑥+8個=80個
⑥＝72個
①=12個とわかる。

(10)答え：5200円
原価：2000円
定価：2000円×4割+2000円=2800円
※慣れれば、2000円×(1+0.4)で計算しましょう
利益：2800円-2000円=800円
売れた9個の利益：800円×9個=7200円
1個売れ残ったので、7200円-2000円=5200円

(11)答え：5740円
原価：50円
定価：50円×(1+0.8)=90円
利益：90円-50円=40円

初日に売れた数：200個×0.3=60個
初日の利益：40円×60個=2400円

2日目の売価：90円×0.9=81円
売価での利益：81円-50円=31円

2日目に売れた数：200個-60個=140個
2日目の利益：31円×140個=4340円

初日と2日目の合計利益：2400円+4340円=5740円

(12)答え：54760円
原価：50円
定価：50円×(1+0.8)=90円
利益：90円-50円=40円

初日に売れた数：2000個×0.4=800個
初日の利益：40円×800個=32000円

ジュースにした数：(2000個-800個)×0.1=120個
ジュースにしたリンゴの仕入れ値の合計：50円×120個=6000円
ジュースの合計代金：5000円
※ジュースにした120個のリンゴで1000円の損をしたことになる

2日目の売価：90円×0.8=72円
売価での利益：72円-50円=22円
2日目に売れた数：2000個-800個-120個=1080個
2日目の利益：22円×1080個=23760円
合計利益：初日の利益＋2日目の利益-ジュースの損失
=32000円+23760円-1000円
=54760円

(13)答え：6割（の利益を見込んで売る場合）}
原価を1とすると、
6割の場合の利益：1.6-1=0.6
7割の場合の利益：1.7×0.9-1=0.53

(14)答え:500円

	最初のお金	使った後のお金の比
兄	3000円	⑤
妹	2000円	③
差	1000円	②

②=1000円とわかるので、
①=500円
使った後に残った兄のお金は
500円×⑤=2500円
3000円-2500円=500

(15)答え：80枚

	最初のシールの枚数	あげた後のシールの枚数
姉	200枚	③
妹	120枚	⑤
和	320枚	⑧

⑧=320枚とわかるので、
①=40枚
あげた後に残った姉のシールの枚数は
40枚×③=120枚
200枚-120枚=80枚

※比の解き方について、下記の記事で詳しく解説しています。
関連記事：【中学受験】「比」の解き方

中学入試：割合の勉強におすすめの問題集（基礎、難関）

ポイントがわかったところで、実際に中学受験の「割合」の演習をして早く解きなれましょう。

おすすめの問題集を紹介します。AmazonのPRリンクをつけているので、リンク先でお得に購入いただけます。

下記リンクは算数嫌いの子を算数好きに変えるRISUのPRです。リンク先で無料体験を申し込めます。

算数が好きになるのには理由があります【RISUきっず】

※関連記事：RISU算数の特長・活用法（小学生向け）と費用を解説

『単元別基本問題集基本の制覇割合―中学入試算数』

単元別基本問題集基本の制覇割合―中学入試算数

出版社：富士教育出版社
レベル：基本～標準（★☆☆）

『中学受験算数・東大卒プロ家庭教師がやさしく教える「割合」キソのキソ改訂3版』

中学受験算数・東大卒プロ家庭教師がやさしく教える「割合」キソのキソ改訂3版 (YELL books)

出版社：エール出版社
レベル：基本～標準（★☆☆）

『Step by step 受験算数比・割合の線分図攻略法』

Step by step 受験算数比・割合の線分図攻略法

出版社：文芸社
レベル：標準（★★☆）

『中学入試実力突破算数計算と一行問題』

地域の模試で偏差値60くらいまでの中学校対策はコチラ↓

中学入試実力突破算数計算と一行問題【基本編】:偏差値55を超える! (受験研究社)

地域の模試で偏差値65くらいまでの中学校対策はコチラ↓

中学入試実力突破算数計算と一行問題【発展編】:偏差値63を超える! (受験研究社)

出版社：増進堂・受験研究社
レベル：『基本編』は「標準（★★☆）」、『発展編』は「標準～難関（★★★）」

『中学入試速ワザ算数文章題』

中学入試速ワザ算数文章題 (シグマベスト)

出版社：文英堂
レベル：標準～難関（★★☆）
特徴：

難関中学の入試問題が速く確実に解ける！

～本書の特長～
【１】目で覚える「ポイントチェック」
学習のポイントをまとめた「ポイントチェック」は、鉛筆、赤ペン、マーカーを使った手書きのノートのような見た目で視覚的に理解しやすくなっています。

【２】別冊の書き込み式問題集
実戦力アップ問題を別冊に載せています。
本冊の「ポイントチェック」を横に置き、ポイントを確認しながら解くこともできます。

【３】実際の答案例を載せた解答
本冊の解答には、実際に問題に書き込んだ「答案例」を載せています。
別冊の問題と同時に開いて見比べることができます。答案のムダを省き、ライバルに差をつける「速ワザ」を身につけられます。
Amazonより引用

『中学入試算数塾技100』

中学入試算数塾技100 新装版 (中学入試塾技)

出版社：文英堂
レベル：標準～難関（★★★）
特徴：

●現役塾講師が、塾だけで教える算数の「塾技」を公開。
●難関中学受験の基礎固めに、入試頻出の解法パターンが1冊で学べるこの本をどうぞ。
わかりやすさはもちろん、使いやすさも追求。短期間での巻き返しも可能にします。
●著者運営サイトにご購入特典があります。
Amazonより引用

割合を得意にする勉強方法3つ

どうすれば割合を得意にできるか。いくつかやり方がありますが、厳選して3つお伝えします。

ぜんぶかけ算からはじめる

割合の問題が出てきたら、とりあえず「全部かけ算からはじめましょう」。

割合の問題で、「割合を求めなさい」という問題はほぼ出ません。

「何人ですか？」「何kgですか？」など、具体的な数字を求めるか、
それをもとにして、「どちらがどれだけ多いか/重いか/安いか」などを求める問題が大半です。

ここで、最初の公式を活用します。割合を求めないのなら、使う公式は下記のどちらかです。

くらべる量＝もとにする量×割合
もとにする量＝くらべる量÷割合

「かけ算」か「わり算」です。割合の問題は、答えを出すまでに何度か計算をしますが、途中式は「くらべる量」を求める計算のほうが多いです。

とりあえずかけ算して答えを求めるようにしましょう。

例題

例えば、下記のような問題です。

【問題】

A. 120人の3割は何人？

B. 50kgの40%は何kg？

C. 1クラス40人のうちが男子で、今日は女子が3人欠席した。今日の出席者で、男子と女子はどちらがどれだけ多い？

【答え】

ご覧のように、かけ算で求められます。

わり算を使う問題で間違ってかけ算を使うと、異様に数字が大きくなります。数字が大きくなると、間違いに気づきやすくなります。

【問題】

A. 120人のうち36人は何割？

B. 20kgは50kgの何%？

C. 1クラス40人のうち、15人が男子。男子は女子の何%いる？

【正しい答え】

【とりあえずかけ算】

A. 120人×36人＝4320割？

B. 20kg×50kg=1000%?

C. 40人-15人＝25人…女子は25人
15人×25人=375=37500%？

「4320割」「1000%」なんて聞いたことないですね。

Cの問題でも、男子より女子が多いのが問題をみれば感覚的にわかりますが、かけ算をすると男子は女子の37500%もいることになってしまいます。

とりあえずかけ算にしてみれば、こうした「明らかに違和感のある大きな数字」になります。この時点で、「あ、違う！」と気づけます。

どうしてもわからないときはかけ算をしてみてください。

比例式を得意にする

2つ目の勉強方法は「比例式を得意にすること」です。

比例式は割合の問題を解くときによく使います。比例式は名前が小難しそうですが、仕組みは単純です。

「＝」（イコール）をはさんで、外にある数字どうし、内にある数字どうしをかけます。

例題

たとえば、下記のような問題でつかえます。

【問題】

ホットケーキをつくるために、薄力粉と砂糖が必要です。ホットケーキ1枚で薄力粉80g、砂糖を20g使います。自宅にある薄力粉300gをすべて使うとすると、砂糖は何g使えばいいでしょうか。

【解答】

薄力粉と砂糖の分量を比で表します。

薄力粉 : 砂糖 = 80 : 20
薄力粉 : 砂糖 = 4 : 1

薄力粉を300g使うという条件を使って比例式で表します。

薄力粉300g : 砂糖□g = 4 : 1
□ × 4 = 300 × 1
□ = 300 ÷ 4
□ = 75g

比例式を使うと、「くらべる量」「もとにする量」といった概念を使いません。

すると、「かけ算かな？」「わり算かな？」と悩む必要がなくなります。

比例式を覚えておけば、とても強い味方になってくれます。

そのためには比の勉強が欠かせません。

問題文に数字を書き込む

3つ目の勉強方法は「問題文に数字を書き込むこと」です。

割合の問題は、問題文に出てきている数字が不十分なのが普通です。問題の設定状況を把握するのに必要な数字を全部問題文に書き込みましょう。

これは平面図形・空間図形の解き方と同じですが、数字を書き込むだけでかなり解きやすくなります。

※関連記事：平面図形・空間図形の解き方

例題

先ほどの例題を使って説明します。

問題

前述のように、薄力粉と砂糖の分量は4:1だとわかりました。わかった時点で問題文にそれを書き入れます。

ホットケーキ1枚で薄力粉80g（④）、砂糖を20g（①）使います。自宅にある薄力粉300g（④）をすべて使うとすると、砂糖（①）は何g使えばいいでしょうか。

のような具合です。

解説文をいくら読んでもピンとこないことってありますよね。算数の解説文が苦手な子は「4:1」といった抽象的な式と「薄力粉300g」といった具体的な数字をつなげて考えるのが苦手です。

式は抽象的でも問題文は「薄力粉300g」のように具体的に書いてくれていますから、新たに把握できた数字を問題文に書き込むと、設定された状況を具体的に把握しやすくなります。

中学受験算数の苦手を克服する方法

中学受験の問題は特殊で、手の込んだ解法が多いです。国語の知識問題や理科・社会でも覚える内容が多く、思うように勉強がはかどらない人はとても多いです。

勉強しているのになかなか解けるようにならない。それには必ず原因があります。考えられる対策を1つ1つ試していくと改善ができます。

復習を増やす

1つ目は、復習を増やす方法です。

中学入試の算数の解き方は大人が解く公務員試験の「数的処理」にも似ており、小学生にはむずかしく感じるものが多いです。

1つ解き方が分かっても次々問題を解くうちに、以前は解けたはずの問題の解き方を忘れてしまいます。

前日解いた問題をもう1度解く
問題集を最初から解きなおしていく

このように、復習する頻度や復習する時間を増やすと忘れにくくなります。

問題集の難易度を下げてみる

現在使っている問題集で苦労されているなら、思い切って問題集の難易度を下げてみましょう。

難関中学を目指されている場合、「むずかしい問題を解かないといけない」と思って難問中心の問題集を使うことがあります。確かに難問を解けるようにならないといけないかもしれませんが、入試までのステップを小さくしてあげると克服しやすくなることがよくあります。

最初は基本問題、慣れてきたら標準問題→応用問題と、問題集の難易度を少し上げます。

演習量や勉強時間は増えますが、解ける問題が確実に増えてくると子どももやりがいを感じるようになります。

個別指導塾を利用・併用する

あれこれ試して効果がなければ、個別指導塾を利用・併用してみましょう。

自宅学習のみで対策されている方は個別指導塾を利用してみる、
集団指導塾で対策されている方は個別指導塾を併用してみるのがおすすめです。

勉強しているのに成績が上がらない原因をまず突き止めて、ピンポイントに対策するほうが早く改善できます。

※関連記事：【中学受験】個別指導塾併用のメリット

家庭教師を利用する

新たに塾に通う時間がない方や通える範囲内に適切な塾がない場合、家庭教師の利用が便利です。

移動時間がゼロなので、その時間を復習にあてたりリラックスする時間にあてたりできます。

また、まだまだ活用されている方は少数派ですが、オンライン家庭教師は中学受験で非常に有効です。対面授業だとなかなか利用できないほど実績のある中学受験指導のプロを利用できます。

【下記リンクはプロ講師による個別指導と、LINEなどで勉強方法の指導やスケジューリングもしてくれる「みんなの塾」のPRです。月17,800円から受講できるので、敷居は高くありません。】

オンラインコース【みんなの塾】

教材は大抵自由ですから、塾に通ってらっしゃる方は塾の教材をオンライン家庭教師との勉強でも使えますし、市販教材や通信教材も使えます。

しかも継続的な利用、単発的な利用どちらも選べます。

オンライン家庭教師をはじめるための準備機材（ヘッドセットくらいですが）や、授業の進め方などを下記の記事で紹介しています。

通信教育を試してみる

塾に通ってみて上手くいかなければ、通信教育を試してみるのも一つの手です。

移動時間がゼロですし、塾に比べて短時間の1回あたりの勉強が短時間に設計されています。「塾と併用」「通信教育単独」のどちらも選べます。

難関中学対策ならZ会

難関中学、最難関中学（首都圏御三家、灘中学、ラサール中学など）を目指しているならZ会がおすすめです。下記のような特長があります。

トータル受講、ライトな受講（要点集中プラン）を選べる
1科目から受講できる
塾と同じかそれ以上の難易度の問題にもチャレンジできる
記述特訓や理科の複雑な計算対策など入試頻出分野の対策講座を取れる

※関連記事：Z会中学受験コースだけで難関中学に合格する方法

下記のZ会のPRリンクから資料請求・無料体験の申し込みができます。

Ｚ会の通信教育　中学受験コース

苦手、嫌いを克服するなら進研ゼミ

中学受験対策の通信教育として進研ゼミも多くの受験生に選ばれています。楽しく、自信をつけながら学べるという特徴があります。

視覚的に理解しやすい授業動画
1回15分の設計で勉強がつづけやすい
赤ペン先生がほめながら添削してくれる
合格実績は4,000名以上

※関連記事：進研ゼミ小学講座の特徴と効果的な利用法

以下の進研ゼミのPRリンクから資料請求や無料体験の申し込みができます。

進研ゼミ小学講座の無料体験はこちら

楽しく算数の先取り学習ができるRISU

中学受験対策には算数の先取りが欠かせません。

算数の先取りをするのに便利な学習道具としてRISU算数という、「算数に特化したタブレット型の通信教育サービス」があります。

ゲームのようにステージをクリアすればするほど算数の問題を解けるようにしていくシステムです。

小学校の勉強先取りはもちろん中学受験の問題もたくさんあり、RISUの会員で四谷大塚の全国小学生学力テストやSAPIXの模試で全国1位を取っている子も出ています。

費用のシステムが分かりにくいので、その解説も含めて下記の記事で紹介しています。

RISU算数の特長・活用法（小学生向け）と費用を解説

以下のRISUのPRリンクから13日間無料体験の申し込みができます。

成績アップの3つの秘密：効果で選ぶなら、RISU算数

先に理科・社会を得意にする

算数で苦労している子なら、先に理科・社会を得意にしておくのもおすすめです。

モチベーションアップ・自信アップにつながりますし、理科・社会の得点が志望校合格に向けて非常に大きな支えになります。

5年生以降になると、算数は実力を伸ばすのに時間がかかるようになります。

勉強内容が受験レベルになってくるため、1問1問解くのに時間がかかりますし、それ以前の学習内容で1つでも穴があると問題集の解説が理解しづらいからです。

それでもじっくり腰をすえて対策すればやがて克服できますが、小学生にとって「こしをすえて」「じっくり取り組む」のはひと苦労です。

「いくら勉強してもどうせ無理」

と、早々にあきらめモードになってしまう子も多く、受験継続のピンチを感じている保護者の方は多いです（テラコヤプラスより）。

そんなときに「自分は理科/社会が得意」と自信を持っていると、勉強のやる気が続きやすいです。

力を発揮しやすい出題傾向の学校を受ける

中学入試の問題は中学校によってまちまちです。

思考力問題中心
記述問題中心
知識問題の配点が高い
計算力をハイレベルに求める

など。上位校だから必ずしも応用問題ばかりとは限りませんし、そうであっても図形など特定分野が得意な子が模試の結果をくつがえして逆転合格を勝ち取るケースはたびたびあります。

模試の偏差値だけで判断せず、志望校の出題傾向をみたり、6年生の春先に解いてみたりして相性を確認してみましょう。

ほかの科目の勉強方法・問題

ほかの科目の勉強方法や問題を下記の記事で案内しています。ぜひ、ご覧ください。