逆比、連比、比例式の解き方と練習問題（中学受験）：比の苦手を克服できる問題集も紹介

Pocket

中学受験の算数で必須の比。苦手にしている人が多い一方で、比のいくつかの解き方をマスターしておくと割合・速さ・図形などの重要単元で大活躍してくれます。

そこで、重要単元で役に立つ比の解き方を3種類ピックアップしました。

逆比
連比
比例式

です。最初に比の解き方をおさらいしてから、これらの解法を用いる問題演習に移ります。

比を克服して、受験算数を得意にしましょう！

【下記バナーは難関中学受験対策で定番のZ会のPRです。塾と併用、Z会単独どちらにも有効です。】

※Z会の中学受験コースのメリットや活用法を下記の記事で紹介しています。
Z会中学受験コースだけで難関中学に合格する方法

比の基本問題
中学入試によく出る比の問題（逆比、連比、比例式）
1. 解答
比の演習におすすめの問題集（基礎、難関）
中学受験算数の苦手を克服する方法
ほかの科目の問題や解き方のコツ
1. 関連

比の基本問題

比の基本的な解き方からおさらいし、逆比・連比・比例式の演習に移ります。

比を簡単な整数にする問題

比は1:2、2:3のような「簡単な整数」にします。

10:20だと、10（前項と呼びます）と20（後項と呼びます）をそれぞれ10で割って、
1:2
にします。

練習で、下記の比を簡単な整数の比にしましょう。

(1)5:10

(2)8:10

(3)1.2:12

(4)0.5:2.5

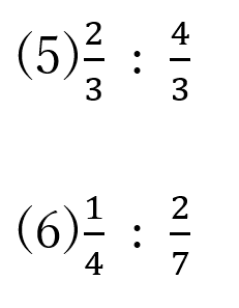
解答

(1)1:2
5と10をそれぞれ5で割ります。

(2)4:5
8と10をそれぞれ2で割ります。

(3)1:10
1.2と12をそれぞれ10倍して12:120にし、
12と120をそれぞれ12で割ります。

(4)1:5
0.5と2.5をそれぞれ10倍して5:25にし、
5と25をそれぞれ5で割ります。

(5)1:2
どちらも3をかけて2:4にし、
2と4をそれぞれ2で割ります。

逆比にする問題

続いて、逆比です。逆比とは「逆数の比」のことを言います。速さの問題で特によく使います。

※関連記事：【中学受験】速さの解き方のコツを解説

1000円持っているとすると、1個200円のアイスなら5個買えて、1個500円のフルーツ大福なら2個買えます。

買える個数がアイス：フルーツ大福=5:2なので、値段の比は5と2を逆数にして下記のように求めます。

練習で、下記の比を逆比にしてみましょう。

(1)2 : 3

(2)1.2 : 12

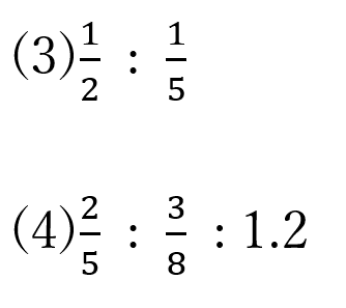
逆比の解答

(1)3 : 2

(2)10 : 1
1.2 : 12=1 : 10　　　　　　　　　　　　

(3)2 : 5　　　

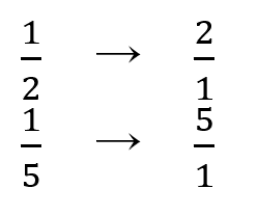
(4)15 : 16 : 5

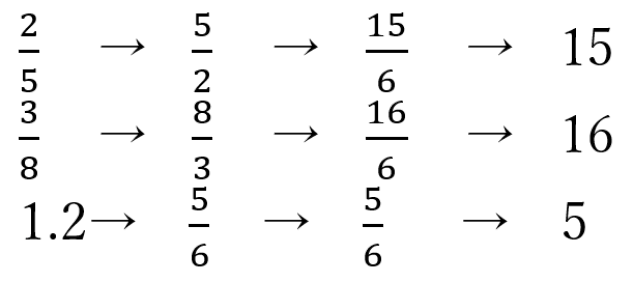
連比を使う問題

A：B=2：3とB：C=3：4を利用して
A：B：C=2：3：4のように3つの値の比を求める場合があります。

これを連比といいます。

A：BとB：Cをみると「Bが共通」しています（どちらの比の式にもBが登場しています）。

共通している項目がどちらの式でも同じ数字ならA:B:C=2:3:4のように並べて書けば終わりですが、大抵の問題は共通している項目が違う数字になっています。

その場合、共通している項目が同じ数字になるように最小公倍数にします。

例えば、A：B=2：3でB：C=4：5の場合、下記のように解きます。

	A	B	C
×4をする	2	3
×3をする		4	5
共通しているBを最小公倍数にする	8	12	15

よって、答えはA：B：C=8：12：15です。

練習で、下記の連比の問題を解いてみましょう。

(1)A：B=2：3、B：C=3：5のとき、A：B：Cを求めなさい。

(2)A：B=2：3、B：C=5：2のとき、A：B：Cを求めなさい。

(3)A：B=2：3、A：C=4：5のとき、A：B：Cを求めなさい。

連比の解答

(1)A：B：C=2：3：5

	A	B	C
	2	3
		3	5
共通しているBが同じ数字	2	3	5

(2)A：B：C=10：15：6

	A	B	C
×5をする	2	3
×3をする		5	2
共通しているBを最小公倍数にする	10	15	6

(3)A：B：C=4：6：5

	A	B	C
×2をする	2	3
	4		5
共通しているAを最小公倍数にする	4	6	5

比例式を使う問題

2：4=4：8のように、簡単な整数にすると＝の左と右が同じになる式を比例式といいます。

この例だと、2：4も4：8も簡単な整数にして1：2になります。

入試問題で使う場合は大抵、2：4=4：□のように一部がわからない場合です。

比例式を解くには（＝□に入る数字を求めるには）、
外側の数字どうし（外項）・内側の数字どうし（内項）をかけ算します。

とりあえずこの計算方法さえ知っておけば比例式は解けます。

2：4=4：□の例だと、

2×□＝4×4
□=16÷2
□=8

と求めます。

早速問題を解いて練習してみましょう。

(1)8：5=16：□

(2)6：□=18：15

(3)12：5=□：15

比例式の解答

(1)10
8×□=16×5
□=80÷8
□=10

(2)5
□×18=6×15
□=90÷18
□=5

(3)36
5×□=12×15
□=180÷5
□=36

中学入試によく出る比の問題（逆比、連比、比例式）

問題. 次の問題を解きましょう。

(1)バナナ1房がリンゴ1個の7割の値段のときバナナ：リンゴの値段を比で表しなさい。

(2)バナナ1房がリンゴ1個の80%の値段のとき、バナナ：リンゴの値段を比で表しなさい。

(3)スーパーに買い物に行ったところ、バナナ1房の値段を3倍するとリンゴ1個の2倍の値段と等しいことがわかった。バナナ：リンゴの値段を比で表しなさい。

(4)スーパーに買い物に行ったところ、バナナ1房の値段の80%がリンゴ1個の6割の値段と等しいことがわかった。バナナ：リンゴの値段を比で表しなさい。

(5)兄と弟が同じ学校に通っている。家から学校に行くまでの時間の比が兄：弟=3：4のとき、兄と弟の速さの比を求めなさい。

(6)10円玉と100円玉の枚数が5:3のとき、10円玉の合計金額と100円玉の合計金額の比を求めなさい。

(7)10円玉と100円玉と500円玉の枚数が2：3：5のとき、10円玉の合計金額と100円玉と500円玉の合計金額の比を求めなさい。

(8)10円玉と100円玉の合計金額の比が3：4のとき、10円玉と100円玉の枚数の比を求めなさい。

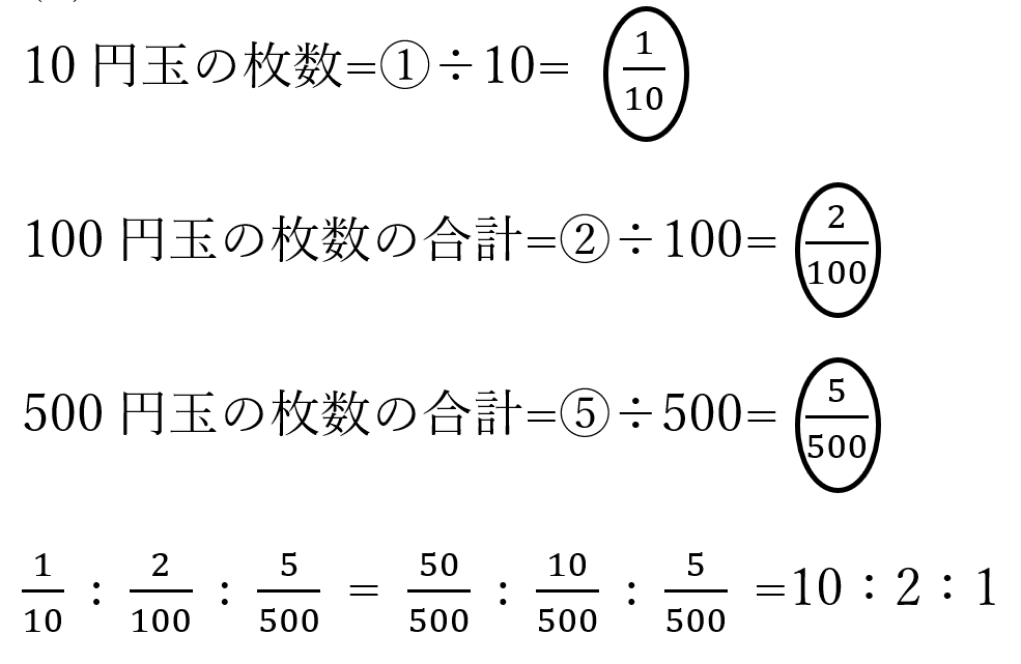
(9)10円玉と100円玉と500円玉の合計金額の比が1：2：5のとき、10円玉と100円玉と500円玉の枚数の比を求めなさい。

(10)3000円を兄・姉・妹の3人でわけます。兄：姉：妹の金額の比が3：2：1になるようにするには、それぞれいくらにすればいいか。

(11)姉・兄・弟でおこづかいの金額を比べたところ、姉：兄＝5：4、兄：弟=3：2の比だった。姉：兄：弟のおこづかいの比を求めなさい。

(12)5000円を姉・兄・妹の3人でわけます。姉：兄＝10：9、姉：妹=5：3になるようにするには、それぞれいくらにすればいいか。

(13)三角形ABCの三つの角度の比が2：3：4のとき、1番大きな角度の大きさを求めなさい。

(14) 直角三角形ABCの三つの角度の比が4：5：9のとき、1番小さな角度の大きさを求めなさい。

(15)ある人は分速100mで15分歩いたところ1500m進んだ。この人が同じ速さで6km歩くには何分かかるか求めなさい。

(16)かおるさんは毎朝、7:40分に家を出発して学校に8時ちょうどに到着している。今朝もいつもどおりの時間に出発したが、出発して5分経ったところで、学校で委員会活動があることを思い出した。あと10分で学校につくようにしないといけないが、いつもより何倍の速さで学校に向かえば間に合うか。

(17)1m200円のリボンを50cm買うといくらになるか。

(18)2000個のアメを100個の箱に均等につめた。20箱で何個のアメが入っているか。

(19)1時間で2分ずつ早く進んでしまう時計がある。午前8時に正しい時刻に時計をセットしたとき、同じ日の午後8時には時計は何時何分をさしているか。

(20)1時間で2分ずつ早く進んでしまう時計がある。午前8時に正しい時刻に時計をセットした。この時計が同じ日の午後8時をさしているとき、正しい時刻は何時何分か。

(21)1時間で5分ずつ早く進んでしまう時計がある。時刻合わせをして午後8時に正しい時刻と照らし合わせたところ、この時計は午後9時をさしていた。時刻合わせをしたのは何時何分か。

解答

(1)7：10

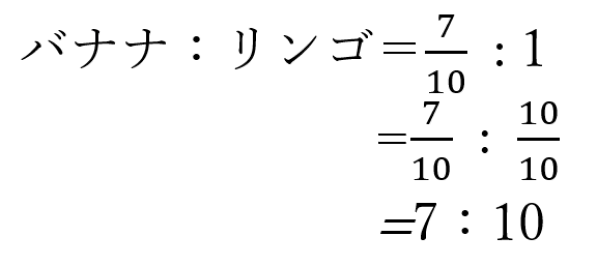
(2)4：5

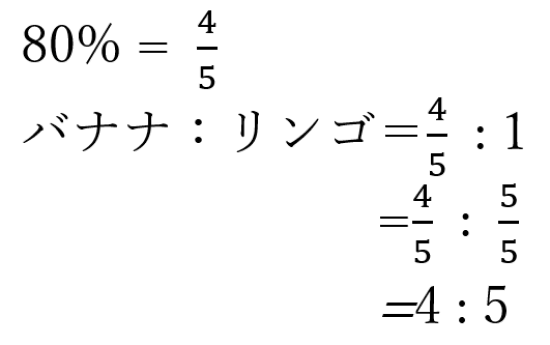
(3)2：3

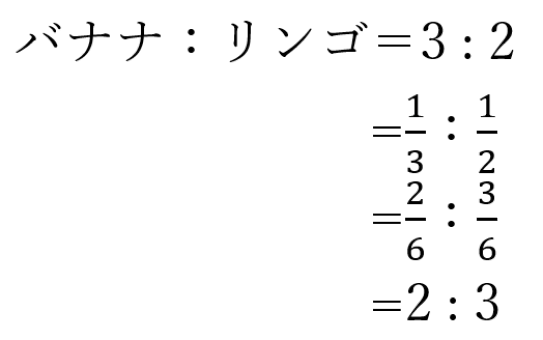
(4)3：4

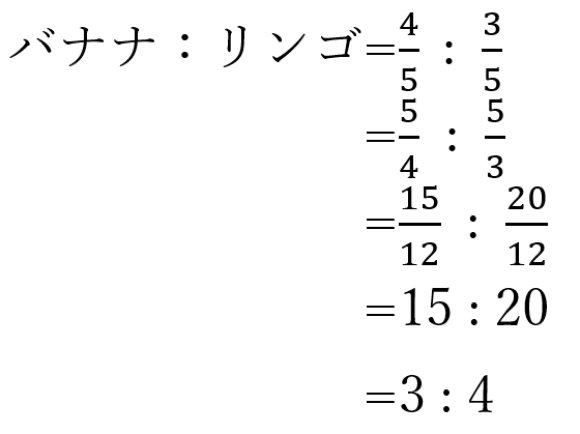
(5)4：3

(6)1：6
10円玉の合計金額=10×⑤=50
100円玉の合計金額=100×③=300
50 : 300= 1 : 6

(7)1：5：125
10円玉の合計金額=10×②=⑳
100円玉の合計金額=100×③=300　
500円玉の合計金額=500×⑤=2500
⑳ : 300 : 2500 = 1 : 15 : 125

(8)15：2

(9)10：2：1

(10)兄：1500円、姉：1000円、妹：500円
3000円÷（③+②+①）=500円
…①が500円になるとわかる
兄：500円×③=1500円
姉：500円×②=1000円
妹：①なので、500円

(11)姉：兄：弟＝15：12：8

	姉	兄	弟
×3をする	5	4
×4をする		3	2
共通している兄を最小公倍数にする	15	12	8

(12)姉：2000円、兄：1800円、妹：1200円

	姉	兄	妹
	10	9
×2をする	5		3
共通している姉を最小公倍数にする	10	9	6

5000円÷（⑩+⑨+⑥）=200円
…①が200円になるとわかる
姉：200円×⑩=2000円
兄：200円×⑨=1800円
妹：200円×⑥=1200円

(13)80°
三角形の内角の和は180°になるので、
②＋③＋④＝180°
⑨＝180°
①＝20°
①が20°なので、一番大きな④の角は
20°×④=80°

(14)40°
直角三角形なので、一番大きな角度は⑨の大きさの角で、90°になる。
④⑤の大きさの角は合計90°（180°-90°）になるので、
④+⑤=90°
⑨＝90°
①=10°
一番小さな角は④の大きさの角なので、
10°×④＝40°

(15)60分
15分：1500m＝□分：6000m
1500m×□分=15分×6000m
□=60分

(17)100円
100cm：200円=50cm：□円
100×□＝200×50
□＝10000÷100
□＝100

(18)400個
2000：100=□：20
100×□＝2000×20
□=40000÷100
□=400

(19)午後8時24分
1時間で2分早く進む＝60分で62分進む。
午前8時から午後8時まで12時間。
60：62=12：□
60×□＝744
□=12.4
60分×0.4=24分なので、午後8時＋24分＝午後8時24分。

(21)午前8時
1時間で5分早く進むということは、
60：5＝12：1の誤差の比になる。
正しい時刻が午後8時のときに故障した時計が午後9時なので、60分早く進んでいることになる。
12：1＝□：60
□＝720
故障した時計が60分早く進む間に、正しい時間は720分過ぎたことになる。
720分÷60分＝12時間
午後8時の12時間前なので、時刻合わせをしたのは午前8時。

比の演習におすすめの問題集（基礎、難関）

ポイントがわかったところで、実際に中学受験の「比」の演習をして早く解きなれましょう。

おすすめの問題集を紹介します。AmazonのPRリンクをつけているので、リンク先でお得に購入いただけます。

『単元別基本問題集基本の制覇比―中学入試算数』

単元別基本問題集基本の制覇比―中学入試算数

面積比はコチラ↓

単元別基本問題集基本の制覇面積比―中学入試算数

出版社：富士教育出版社
レベル：基本～標準（★☆☆）

『比の基礎 (思考力算数練習帳シリーズ 41)』

比の基礎 (思考力算数練習帳シリーズ 41)

出版社：株式会社認知工学
レベル：基本～標準（★☆☆）

『中学入試実力突破算数計算と一行問題』

地域の模試で偏差値60くらいまでの中学校対策はコチラ↓

中学入試実力突破算数計算と一行問題【基本編】:偏差値55を超える! (受験研究社)

地域の模試で偏差値65くらいまでの中学校対策はコチラ↓

中学入試実力突破算数計算と一行問題【発展編】:偏差値63を超える! (受験研究社)

出版社：増進堂・受験研究社
レベル：『基本編』は「標準（★★☆）」、『発展編』は「標準～難関（★★★）』

『中学入試速ワザ算数文章題』

中学入試速ワザ算数文章題 (シグマベスト)

出版社：文英堂
レベル：標準～難関（★★☆）
特徴：

難関中学の入試問題が速く確実に解ける！

～本書の特長～
【１】目で覚える「ポイントチェック」
学習のポイントをまとめた「ポイントチェック」は、鉛筆、赤ペン、マーカーを使った手書きのノートのような見た目で視覚的に理解しやすくなっています。

【２】別冊の書き込み式問題集
実戦力アップ問題を別冊に載せています。
本冊の「ポイントチェック」を横に置き、ポイントを確認しながら解くこともできます。

【３】実際の答案例を載せた解答
本冊の解答には、実際に問題に書き込んだ「答案例」を載せています。
別冊の問題と同時に開いて見比べることができます。答案のムダを省き、ライバルに差をつける「速ワザ」を身につけられます。
Amazonより引用

『中学入試算数塾技100』

中学入試算数塾技100 新装版 (中学入試塾技)

出版社：文英堂
レベル：標準～難関（★★★）
特徴：

●現役塾講師が、塾だけで教える算数の「塾技」を公開。
●難関中学受験の基礎固めに、入試頻出の解法パターンが1冊で学べるこの本をどうぞ。
わかりやすさはもちろん、使いやすさも追求。短期間での巻き返しも可能にします。
●著者運営サイトにご購入特典があります。
Amazonより引用

中学受験算数の苦手を克服する方法

中学受験の問題は特殊で、手の込んだ解法が多いです。国語の知識問題や理科・社会でも覚える内容が多く、思うように勉強がはかどらない人はとても多いです。

勉強しているのになかなか解けるようにならない。それには必ず原因があります。考えられる対策を1つ1つ試していくと改善ができます。

復習を増やす

1つ目は、復習を増やす方法です。

中学入試の算数の解き方は大人が解く公務員試験の「数的処理」にも似ており、小学生にはむずかしく感じるものが多いです。

1つ解き方が分かっても次々問題を解くうちに、以前は解けたはずの問題の解き方を忘れてしまいます。

前日解いた問題をもう1度解く
問題集を最初から解きなおしていく

このように、復習する頻度や復習する時間を増やすと忘れにくくなります。

問題集の難易度を下げてみる

現在使っている問題集で苦労されているなら、思い切って問題集の難易度を下げてみましょう。

難関中学を目指されている場合、「むずかしい問題を解かないといけない」と思って難問中心の問題集を使うことがあります。確かに難問を解けるようにならないといけないかもしれませんが、入試までのステップを小さくしてあげると克服しやすくなることがよくあります。

最初は基本問題、慣れてきたら標準問題→応用問題と、問題集の難易度を少し上げます。

演習量や勉強時間は増えますが、解ける問題が確実に増えてくると子どももやりがいを感じるようになります。

個別指導塾を利用・併用する

あれこれ試して効果がなければ、個別指導塾を利用・併用してみましょう。

自宅学習のみで対策されている方は個別指導塾を利用してみる、
集団指導塾で対策されている方は個別指導塾を併用してみるのがおすすめです。

勉強しているのに成績が上がらない原因をまず突き止めて、ピンポイントに対策するほうが早く改善できます。

※関連記事：【中学受験】個別指導塾併用のメリット

家庭教師を利用する

新たに塾に通う時間がない方や通える範囲内に適切な塾がない場合、家庭教師の利用が便利です。

移動時間がゼロなので、その時間を復習にあてたりリラックスする時間にあてたりできます。

また、まだまだ活用されている方は少数派ですが、オンライン家庭教師は中学受験で非常に有効です。対面授業だとなかなか利用できないほど実績のある中学受験指導のプロを利用できます。

【下記リンクはプロ講師による個別指導と、LINEなどで勉強方法の指導やスケジューリングもしてくれる「みんなの塾」のPRです。月17,800円から受講できるので、敷居は高くありません。】

オンラインコース【みんなの塾】

教材は大抵自由ですから、塾に通ってらっしゃる方は塾の教材をオンライン家庭教師との勉強でも使えますし、市販教材や通信教材も使えます。

しかも継続的な利用、単発的な利用どちらも選べます。

オンライン家庭教師をはじめるための準備機材（ヘッドセットくらいですが）や、授業の進め方などを下記の記事で紹介しています。

通信教育を試してみる

塾に通ってみて上手くいかなければ、通信教育を試してみるのも一つの手です。

移動時間がゼロですし、塾に比べて短時間の1回あたりの勉強が短時間に設計されています。「塾と併用」「通信教育単独」のどちらも選べます。

難関中学対策ならZ会

難関中学、最難関中学（首都圏御三家、灘中学、ラサール中学など）を目指しているならZ会がおすすめです。下記のような特長があります。

トータル受講、ライトな受講（要点集中プラン）を選べる
1科目から受講できる
塾と同じかそれ以上の難易度の問題にもチャレンジできる
記述特訓や理科の複雑な計算対策など入試頻出分野の対策講座を取れる

※関連記事：Z会中学受験コースだけで難関中学に合格する方法

下記のZ会のPRリンクから資料請求・無料体験の申し込みができます。

Ｚ会の通信教育　中学受験コース

苦手、嫌いを克服するなら進研ゼミ

中学受験対策の通信教育として進研ゼミも多くの受験生に選ばれています。楽しく、自信をつけながら学べるという特徴があります。

視覚的に理解しやすい授業動画
1回15分の設計で勉強がつづけやすい
赤ペン先生がほめながら添削してくれる
合格実績は4,000名以上

※関連記事：進研ゼミ小学講座の特徴と効果的な利用法

以下の進研ゼミのPRリンクから資料請求や無料体験の申し込みができます。

進研ゼミ小学講座の無料体験はこちら

楽しく算数の先取り学習ができるRISU

中学受験対策には算数の先取りが欠かせません。

算数の先取りをするのに便利な学習道具としてRISU算数という、「算数に特化したタブレット型の通信教育サービス」があります。

ゲームのようにステージをクリアすればするほど算数の問題を解けるようにしていくシステムです。

小学校の勉強先取りはもちろん中学受験の問題もたくさんあり、RISUの会員で四谷大塚の全国小学生学力テストやSAPIXの模試で全国1位を取っている子も出ています。

費用のシステムが分かりにくいので、その解説も含めて下記の記事で紹介しています。

RISU算数の特長・活用法（小学生向け）と費用を解説

以下のRISUのPRリンクから13日間無料体験の申し込みができます。

成績アップの3つの秘密：効果で選ぶなら、RISU算数

先に理科・社会を得意にする

算数で苦労している子なら、先に理科・社会を得意にしておくのもおすすめです。

モチベーションアップ・自信アップにつながりますし、理科・社会の得点が志望校合格に向けて非常に大きな支えになります。

5年生以降になると、算数は実力を伸ばすのに時間がかかるようになります。

勉強内容が受験レベルになってくるため、1問1問解くのに時間がかかりますし、それ以前の学習内容で1つでも穴があると問題集の解説が理解しづらいからです。

それでもじっくり腰をすえて対策すればやがて克服できますが、小学生にとって「こしをすえて」「じっくり取り組む」のはひと苦労です。

「いくら勉強してもどうせ無理」

と、早々にあきらめモードになってしまう子も多く、受験継続のピンチを感じている保護者の方は多いです（テラコヤプラスより）。

そんなときに「自分は理科/社会が得意」と自信を持っていると、勉強のやる気が続きやすいです。

力を発揮しやすい出題傾向の学校を受ける

中学入試の問題は中学校によってまちまちです。

思考力問題中心
記述問題中心
知識問題の配点が高い
計算力をハイレベルに求める

など。上位校だから必ずしも応用問題ばかりとは限りませんし、そうであっても図形など特定分野が得意な子が模試の結果をくつがえして逆転合格を勝ち取るケースはたびたびあります。

模試の偏差値だけで判断せず、志望校の出題傾向をみたり、6年生の春先に解いてみたりして相性を確認してみましょう。

ほかの科目の問題や解き方のコツ

ほかの科目の勉強方法や問題を下記の記事で案内しています。ぜひ、ご覧ください。

【算数】

割合の解き方
　中学入試によく出る割合の問題
 比の解き方
　中学入試によく出る比の問題
 速さの解き方
　中学入試によく出る速さの問題
 平面図形・空間図形の解き方

【国語】

【中学受験】国語の勉強法と入試出題傾向を解説
 【中学受験】国語長文読解を短期間で伸ばす勉強法
 中学入試によく出る漢字・熟語・慣用句・ことわざの問題
 記述問題の書き方と勉強方法
 おすすめの記述・作文問題集

【理科】

【中学受験】理科を得意にできる勉強方法
 【中学受験】理科のおすすめ問題集
 中学入試の理科によく出る問題の一問一答
 中学入試理科でよく出る問題の語呂合わせ一覧
 中学受験の理科でよく出る記述問題
 中学入試の理科でよく出る計算問題の公式一覧とおすすめの計算問題集

【社会】

【中学受験】社会で貯金を20点つくる勉強法を紹介
 中学入試の社会によく出る問題の一問一答
 中学受験の社会によく出る年号・年代の語呂合わせ
 【中学受験】歴史の流れを時代別に解説
 【中学受験】社会のおすすめ問題集

【下記バナーは難関中学受験対策で定番のZ会のPRです。バナーをクリックするとZ会のHPに移動できます。】