中学受験の算数は小学校で習わない単元や、小学校で習った単元をさらに応用させている単元がたくさんあります。
なかでも「速さ」は入試の中心であり、得意な子は一段と合格に近づけます。
速さを苦手にしている子は算数自体を苦手にしていることが多いです。
中学、高校の数学にもつながる重要な単元でもあるので、ここで速さを得意にしておきたいですね。
そこで、今回の記事では
- 速さが苦手になる理由
- どうすれば速さが得意になるか
- 頻出問題の解法
を解説します。
※関連記事:中学受験算数の勉強法
※Z会の中学受験コースのメリットや活用法を下記の記事で紹介しています。
Z会中学受験コースだけで難関中学に合格する方法
速さの問題のポイント
まず、速さがどういう単元なのか簡単におさらいします。
速さというのは、「一定時間あたりに進む距離」のことです。
「速さ」という名前の単元ですが、速さ・距離・時間の3つの用語が中心になります。
単位変換が重要
速さも時間も距離もたくさん単位があり、距離と時間の単位に応じて表し方が変わります。この「単位変換」は、速さの問題で大きなポイントのひとつです。
以下の距離・時間の単位変換を覚えておきましょう。
【距離】1km=1000m
【時間】1時間=60分=3600秒
時速・分速・秒速の求め方
速さの単元をややこしく感じる大きな原因のひとつが時速・分速・秒速です。
それぞれ、以下の表のように求めます。
| 時速 | 1時間あたり進む速さ | 距離(km)÷〇時間 |
| 分速 | 1分あたり進む速さ | 距離(m)÷〇分 |
| 秒速 | 1秒あたり進む速さ | 距離(m)÷〇秒 |
また、時速⇔分速⇔秒速の変換は、時速を中心に説明すると以下のように計算します。
時速72kmをもとにして、分速・秒速で表すと下記の表のようになります。
| 分速(時速÷60) | 秒速(分速÷60) | |
| 時速72kmと同じ速さ | 分速1200m (=分速1km) | 秒速20m |
単位の変換は速さの問題を解くうえで必須です。
基本問題でたっぷり練習して、計算方法を思い出さなくてもいいぐらいまで慣れておきましょう。
速さを得意にするコツ
家庭ですぐできる「速さ」を得意にする方法をお伝えします。
単位をそろえる
速さの問題を解くときは、「まず単位を1つにそろえましょう」。
速さをむずかしく感じる理由の1つは、単位互換です。
速さで必要な単位互換はむずかしいわけでもなく、覚えきれないほどたくさんの単位が出てくるわけでもありません。
何が厄介なのかというと、複数の単位が一緒に出てくると文章で述べられている状況をイメージしにくくなるのです。
たとえば、分速200mで走る人と、分速150mで走る人はどちらが速いかと聞かれると、すぐわかります。300mのほうですよね。
では、分速200mと時速9kmならどちらが速いでしょうか。パッとは答えられないです。
分速200mを時速12kmにするか、時速9kmを分速150mに変換してくらべるはずです。
この、単位をそろえる作業を必ずしておきましょう。
具体的には、「km⇔m」、「時間⇔分⇔秒」をそろえます。何mでしょうか?と聞かれていたら、mに合わせるようにすると計算が減って便利です。
あるいは、自分が感覚的に理解しやすい単位に合わせても大丈夫です。
何時間でしょうか?と聞かれていても、分のほうが把握しやすければいったんすべて分になおしてしまいます。最後に分を時間に変換すればOKです。
割合の復習をする
速さが苦手な人はたいてい、割合も苦手です。前述のように、割合と速さは問題の構成(解き方)がよく似ています。
割合が苦手だと速さもなかなか克服できません。基本的な問題だけでも復習して解けるようにしておきましょう。
【問題】「30人のクラスで6割が女子。女子は何人?」
【答え】30人×0.6=18人
【問題】「100個のリンゴを20人の子どもで分けたら1人何個?」
【答え】「100個÷20人=5個」
という2つのパターンをサッと解けるように繰り返し練習しましょう。
※関連記事:割合の解き方
※関連記事:入試によく出る割合の問題・解説
速さ、割合を日常生活で頻繁につかう
割合や速さは日常生活でもよく登場します。日常生活で頻繁につかうとようにすると、早く慣れられます。
【日常生活で割合や速さをつかう例】- スーパーで買った3本の魚入りのパック。家族4人でわけると1人あたりどれくらいの量になるか?
- 298円の魚のパックが30円割引されている。何割引かれていて、何%引かれている?もともとの値段から何割になっていて、何%になっている?
- 家から学校までの距離はどれくらいかな?を調べる(google mapで調べられます)。1.2kmなら、それをmに変換する。
- 家から学校まで15分かかっているなら、分速何mなのかを計算する。その後、分速何km、時速何km、時速何mも計算してみる。
- 家から学校まで歩く速さを2倍にしたら何分で着く?遅刻しそうなとき、途中まで自転車に乗って分速300mで行ったら、何分で着く?
このような感じで、何か数字をみたらそれをつかって練習します。
この作業を日々繰り返しておくと、2週間もあれば割合や速さにかなり慣れます。
通信教育を試してみる
塾に通ってみて上手くいかなければ、通信教育を試してみるのも一つの手です。
移動時間がゼロですし、塾に比べて短時間の1回あたりの勉強が短時間に設計されています。「塾と併用」「通信教育単独」のどちらも選べます。
難関中学対策ならZ会
難関中学、最難関中学(首都圏御三家、灘中学、ラサール中学など)を目指しているならZ会がおすすめです。下記のような特長があります。
- トータル受講、ライトな受講(要点集中プラン)を選べる
- 1科目から受講できる
- 塾と同じかそれ以上の難易度の問題にもチャレンジできる
- 記述特訓や理科の複雑な計算対策など入試頻出分野の対策講座を取れる
※関連記事:Z会中学受験コースだけで難関中学に合格する方法
苦手、嫌いを克服するなら進研ゼミ
中学受験対策の通信教育として進研ゼミも多くの受験生に選ばれています。楽しく、自信をつけながら学べるという特徴があります。
- 視覚的に理解しやすい授業動画
- 1回15分の設計で勉強がつづけやすい
- 赤ペン先生がほめながら添削してくれる
- 合格実績は4,000名以上
※関連記事:進研ゼミ小学講座の特徴と効果的な利用法
楽しく算数を勉強するならRISU
算数に苦手意識のある子を「算数好き」にする通信教育としてRISUが注目を集めています。
ゲームのようにステージをクリアすればするほど算数の問題を解けるようにしていくシステムです。
小学校の勉強先取りはもちろん中学受験の問題もたくさんあり、RISUの会員で四谷大塚の全国小学生学力テストやSAPIXの模試で全国1位を取っている子も出ています。
費用のシステムが分かりにくいので、その解説も含めて下記の記事で紹介しています。
中学受験でよく出る速さの応用問題3パターン
速さの問題パターンは限られています。よく出る3パターンの問題と解き方を説明します。
速さを変える問題の解き方
1つ目のパターンは速さのオーソドックスなタイプで、速さ・時間・距離をシンプルに問う問題です。
1人で移動していますが、速さを変えて移動します。
【問題】花子さんは毎朝同じ時刻に家を出て学校に向かいます。分速80mで歩くと8時25分に着きますが、今朝は用事があったのでいつもと同じ時刻に家を出て分速100mで歩いたところ、8時15分に学校に着きました。花子さんが家を出る時刻は何時何分ですか。
【解説】問題文をみたときに、速さ・時間・距離を下記の3つにわけます。
- 一定のもの
- 変化するもの
- 求めたいもの
問題文を読むと、以下のようになります。
- 一定のもの:(距離)家から学校までの距離
- 変化するもの:(速さ)分速80m→分速100m
- 求めたいもの:(時間)□に置き換える
つづいて、問題文の状況から「求めたいもの」を式にします。
いつもは家から学校まで「□分」かかっているので、
今朝は家から学校まで「□分-10分」と表せます。
さらに、これを使って比例式をつくります。
このとき、「距離が一定なら時間と速さの比は逆になる」ことを覚えておきましょう。
一定のものが時間か速さであれば、比は逆になりません。
比例式は下記のようになります。
分速80m:分速100m=□分―10分:□分
100×□=800-80×□
100×□-80×□=800
20×□=800
□=800÷20
□=40
いつも家から学校までの移動にかかる時間が40分とわかりました。
40分かけて8時25分に到着しているので、家を出る時刻は、
7時45分
になります。
2人が移動して「出会う」問題の解き方
2つ目のパターンは、2人が向かい合って移動してどこかで「出会う」問題です。
【問題】兄は駅を出発して分速80mで家に向かっています。弟は家を出発して駅に向かって分速70mで歩いています。駅と家は1.5km離れています。兄と弟が出会うのは出発してから何分後ですか。
【解説】向かい合って進むので、下記のようなイメージになります。

まず、速さ・時間・距離を求めましょう。
- 速さ:分速150m(兄と弟の合計の速さ:80m+70m)
- 時間:求めたいものなので□にします
- 距離:1500m(1.5kmを単位変換)
これをもとにして式をつくります。
□=1500m÷分速150m
□=10分
というわけで、「10分後に出会う」と答えがでました。
2人が移動して「追いつく」問題の解き方
3つ目のパターンは、2人が同じ方向に向かって別々の時間に出発し、後から出発した人がどこかで「追いつく」問題です。
【問題】兄が家から駅に向かって分速60mで出発しました。兄の忘れ物に気づいた弟が、兄が出発してから10分後に兄を追いかけて分速120mで出発しました。弟は何分後に兄に追いつきますか。
【解説】今度は同じ方向に向かいます。下記のようなイメージです。

速さ・時間・距離を求めましょう。
- 速さ:分速60m(兄と弟の速さの差:120m-60m)
- 時間:求めたいものなので□にします
- 距離:600m(10分間に兄が進んだ距離:分速60m×10分)
これをもとに式をつくります。
□=600m÷分速60m
□=10分
というわけで、「10分後に出会う」と答えがでました。
向かい合って進む場合と、同じ方向に向かい合って進む場合の「速さ」の求め方を間違わないように気をつけましょう。
※関連記事:中学入試によく出る「速さ」の問題・「通過算」の問題
速さの演習におすすめの問題集
ポイントがわかったところで、実際に中学受験の「速さ」の演習をして早く解きなれましょう。
基本からしっかり練習できる、おすすめの問題集を3冊紹介します。
『速さと旅人算―速さの考え方が身につく』

速さと旅人算―速さの考え方が身につく (サイパー思考力算数練習帳シリーズ)
出版社:株式会社認知工学
レベル:基本~標準(★☆☆)
特徴:
速さの問題を基本からたくさん演習できます。
解説も丁寧なので苦手な人が受験レベルまで速さを得意にできます。
『中学入試 分野別集中レッスン 算数 速さ』

中学入試 分野別集中レッスン 算数 速さ (中学入試分野別集中レッスン)
計算練習編もあります↓

中学入試 分野別集中レッスン 算数 計算 (中学入試分野別集中レッスン)
「規則性」編もあります↓

中学入試 分野別集中レッスン 算数 規則性 (中学入試分野別集中レッスン)
出版社:文英堂
レベル:基本~標準(★☆☆)
特徴:
弱点克服が中学入試突破の最大のカギ!
「苦手」分野を「短期間」で「集中ケア」する問題集!【1】速さの解き方・コツが短期間で身につく!
速さの問題に特化して掲載しているので、
効率的に点数をアップさせることができます。【2】 例題・ポイントで確認,練習問題で定着!
例題とポイントで学習内容やコツを確認し、
書き込み式の練習問題に取り組むことで、
ひとりで解ける力がつきます。【3】丁寧な解説で,着実にレベルアップ!
Amazonより引用
正しい解法が身につくように、
例題と練習問題には丁寧な解説を載せているので、
中学入試算数の考え方・解き方をしっかり学習できます。
『中学入試 でる順過去問 算数文章題』

中学入試 でる順過去問 算数文章題 合格への368問 四訂版 (中学入試でる順)
出版社:旺文社
レベル:標準(★★☆)
特徴:
「でる順」だから効率的!
近年の中学入試を徹底的に分析し、頻出度の高い問題を「でる順」に掲載しました。入試によくでる本当に重要なものから学習することができます。ステップ式で得点力UP!
1つの単元は「まとめのページ」→「入試問題でチェック」の2ステップで構成されているので、無理なく着実に合格への力をつけることができます。線分図・面積図の描きかたも学べる!
中学入試で必須の線分図や面積図を使う問題は,単元の最初で線分図や面積図の描きかたを学べるようになっています。・入試の傾向と対策がわかる「中学入試分析」を巻頭に特集
Amazonより引用
・くわしい別冊解答・解説で疑問を解決
受験算数のなかでの速さの重要性
そもそも、受験算数にはどのような単元があるのでしょうか。表にして確認しましょう。
| 単元名 | 単元ごとの問題種別 |
| 和と差 | ■平均に関する問題 ■和差算と分配算 ■消去算 ■年令算 ■やりとりの問題は「割合に関する問題の一覧」内にあります。 ■とりちがえの問題 ■差集め算の問題 ■集合の問題 ■つるかめ算に関する問題 ■いもづる算(つるかめ算の応用) |
| 割合 | ■割合の3用法とその応用 ■割合のやりとり算 ■割合のつるかめ算 ■相当算(還元算) ■分配算 ■倍数算 ■売買損益 ■食塩水の問題 ■比の基本問題 |
| 平面図形 | ■角度や面積を求める ■対角線の本数 ■面積と辺の比 ■相似な図形 ■円とおうぎ形 ■正六角形の分割 ■図形の折り返し ■図形の平行移動 ■回転移動・転がり移動 ■格子点上の問題 ■図形の構成 ■影の問題 ■図形上の点の移動 |
| 数の性質 | ■倍数と約数の問題 ■わり算のあまりと等差数列 ■最大公約数と最小公倍数 ■素因数分解の問題 ■既約分数の個数 ■四捨五入とその範囲 ■分数と小数の応用 ■n進法に関する問題 ■整数の分解 |
| 速さ | ■速さと道のり(基本) ■往復の平均の速さ ■速さと比の問題(速さと比1) ■速さのつるかめ算 ■旅人算に関する問題 ■旅人算と比(速さと比2) ■旅人算とダイヤグラム(速さと比2) ■円周上の旅人算(速さと比3) ■図形上の点の移 ■時計算 ■通過算 ■歩幅と歩数 ■動く歩道 ■エスカレーターの問題 ■流水算 |
| 仕事 | ■仕事算(のべ量) ■仕事算(穴のあいた水そう) ■ニュートン算 |
| 立体図形 | ■複合立体の求積 ■展開図の応用(立体表面上の最短距離) ■投影図の応用 ■(立体)立方体の切断 ■立体の構成の問題 ■積み木の投影図 ■立体に色をぬりばらばらにする ■図形の基本問題 ■容器と水量(水量変化と水深) ■サイコロの問題 |
| 数列と規則性 | ■植木算 ■周期算 ■曜日の問題 ■フィボナッチ数列 ■等差数列 ■階差数列 ■群数列 ■いろいろな数列 ■三角数 ■数表の問題 ■方陣算 |
ぜんぶで80種類の問題があります。速さはそのなかで15種類、全体の約2割にあたります。
この2割を得意にできると、得点のうえでも気持ちの面でも大きいですね。
5、6年生で速さが苦手になる
ところが速さを苦手にしている子は多いうえに、学年が上がるにつれて苦手になっていく子が多い単元なのです。
下記のグラフをご覧ください。
全国の中学受験生を対象に、小学校3年生から6年生がどの単元を苦手にしているかを調査した結果です。
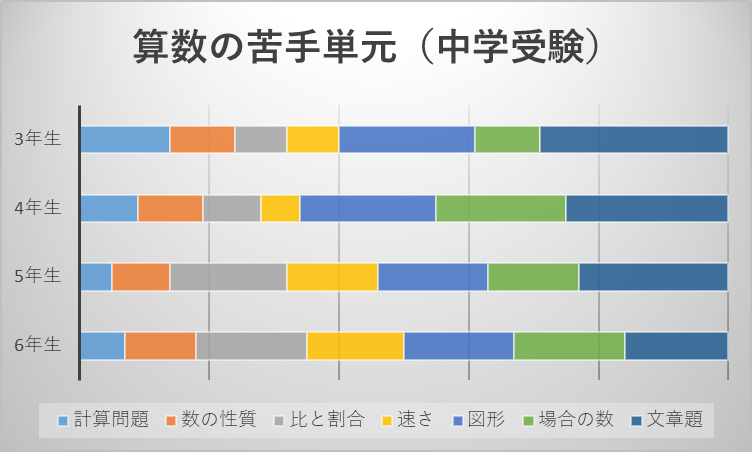
学年があがるにつれて苦手な子が減っていく単元、
逆に苦手な子が増えていく単元があります。
【苦手ではなくなっていく単元】
計算・図形・文章題
【苦手になっていく単元】
数の性質・比と割合・速さ・場合の数
3-4年生速さの苦手な子は少ないほうですが、
5-6年生になると苦手な子は2倍ほどになっています。
同様の変化をしているのが「割合」です。速さでは、割合が重要な役割を担っています。
速さが苦手になる理由
速さが苦手な子は、なぜ苦手になったのでしょうか。原因は3つあります。
割合が苦手
苦手になった理由の1つ目は、「割合」です。
先述のように、学年が上がると苦手になる子がふえていく単元は3つありますが、いずれの単元も割合が重要な役割を担っています。
速さの場合、計算のすべてに割合がつかわれています。
たとえば下記の表のような具合です。割合の問題の解き方を同じ解き方を速さでもしています。
| 割合 | 速さ | 問題の構成 | |
| 問題① | 20個のリンゴを4人で分けると、1人何個? | 20kmの道のりを時速4kmで歩いたら、何時間かかる? | 全部で〇〇あるのを△△でわけると、××になる |
| ―問題①の答え | 20個÷4人=5個 | 20km÷時速4km=5時間 | |
| 問題② | 1人4個ずつのリンゴを持ち寄ったら、5人で何個になる? | 1時間あたり4kmの速さで歩いたら、5時間で何km進む? | △△ずつが××あると、全部で〇〇になる |
| ―問題②の答え | 4個×5人=20個 | 4km×5時間=20km |
問題①、問題②はそれぞれ割合と同じ考え方を速さでもつかっています。
割合がわかっていると速さもとてもわかりやすくなります。逆に、割合がわからないと速さもやはりわからなくなります。
「はじき(みはじ)」にいつまでも頼っている
割合と速さは同じ考え方をしているから、割合がわからないと速さもわからないと説明しました。
1つの単元がわからなくても、学校も集団塾も次の単元に授業を進めざるを得ません。割合がわからないのに、速さをどうやって解けるようにすればいいのか。
そこで生み出されたのが「はじき(はやさ・じかん・きょり)」、
もしくは「みはじ(みちのり・はやさ・じかん)」の法則です。下記の画像です。
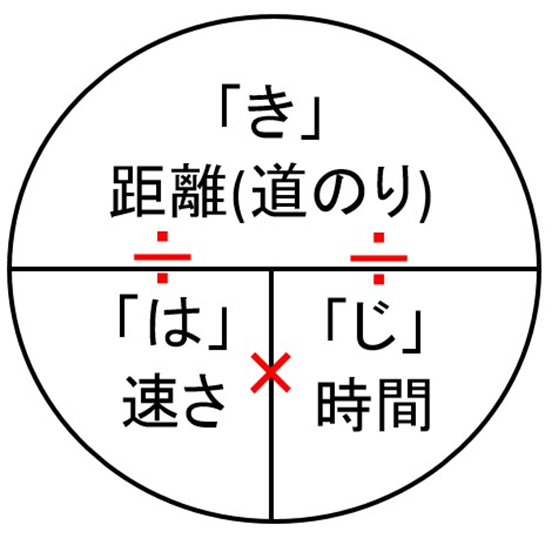
この公式をつかえば、割合がわからなくても機械的に答えを求められます。とても便利でつかいやすい法則なのですが、これが速さを理解できなくしている要因です。
この公式をつかうと、基本問題は楽々解けるようになります。
「速さって簡単!」と自信を持てていいのですが、問題条件がちょっと複雑になると、これが間違いのもとになります。
よくみられるのは、単位が違う場合です。
前述のように、速さの問題には単位がいくつも出てきます。同じ問題で以下のように出てきます。
【問題】車に乗って時速80kmで進むと、30分後には何km進んでいる?
【答え】30分は0.5時間なので、
80km×0.5時間=40km
【「はじき」で解く】速さ×時間=距離に当てはめると、
(速さ)80km×(時間)30分=(距離)2400km
はじきの法則をそのまま当てはめるのに慣れてしまうので、こんな感じに答えを出してしまいます。
2400kmだと本州を縦断できる距離です。30分では無理なはずですが、「法則にあてはめる」勉強に慣れてしまうと、この解答に違和感がなくなります。
それまでどおり問題を解いて急に間違いが多発するので、
「速さはむずかしい。わからない」と苦手意識を持ってしまいます。
単位互換が苦手
速さが苦手になる3つ目の理由は、単位互換です。
先ほど説明したなかにも出てきたように、
「km→m」「時間→分」
のように単位を変換する作業です。
慣れればこの作業はどうってことないのですが、小学生の間はまだまだ不慣れな子が多いです。
1時間は何分?と聞かれると、多くの小学生は「60分」と苦も無く答えられます。
ですが、単位互換を含めていくつもの条件が1つの文章に入っていると混乱してしまい、「3分」を「180時間」にして計算したりします。
ほかの科目の問題や解き方のコツ
ほかの科目の勉強方法や問題を下記の記事で案内しています。ぜひ、ご覧ください。
【算数】割合の解き方
中学入試によく出る割合の問題
比の解き方
中学入試によく出る比の問題
速さの解き方
中学入試によく出る速さの問題
平面図形・空間図形の解き方
【国語】【中学受験】国語の勉強法と入試出題傾向を解説
【中学受験】国語長文読解を短期間で伸ばす勉強法
記述問題の書き方と勉強方法
おすすめの記述・作文問題集
【理科】【中学受験】理科を得意にできる勉強方法
【中学受験】理科のおすすめ問題集
中学入試の理科によく出る問題の一問一答
中学入試理科でよく出る問題の語呂合わせ一覧
中学受験の理科でよく出る記述問題
中学入試の理科でよく出る計算問題の公式一覧とおすすめの計算問題集
【社会】【中学受験】社会で貯金を20点つくる勉強法を紹介
中学入試の社会によく出る問題の一問一答
中学受験の社会によく出る年号・年代の語呂合わせ
【中学受験】歴史の流れを時代別に解説
【中学受験】社会のおすすめ問題集
まとめ
速さは、受験算数のなかで1、2を争うほど苦手にしている受験生が多い単元です。
入試頻出であり、全単元のなかでも2割も占めています。
速さを得意にできれば算数に対して自信を持てますし、合格を勝ち取るための大きな武器にできます。
速さを克服するには割合を使いなれ、単位を合わせるようにしましょう。
この2点をマスターすれば、比をつかって解く方法や線分図・面積図をつかう方法も使いこなせるようになります。
また、特定の単元でどうしても詰まってしまう場合は、家庭教師をスポット的に利用すると便利です。
※関連記事:中学受験での家庭教師の利用法
※関連記事:オンライン家庭教師の特徴・始め方


コメント